Giải bài tập Toán 10 Bài tập cuối chương 4

A. Trắc nghiệm

Bài 4.27 trang 71 Toán 10 Tập 1: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?

A. $\overrightarrow{u}=\left(2;3\right)$ và $\overrightarrow{v}=\left(\frac{1}{2};6\right)$.

B. $\overrightarrow{a}=\left(\sqrt{2};6\right)$ và $\overrightarrow{b}=\left(1;3\sqrt{2}\right)$.

C. $\overrightarrow{i}=\left(0;1\right)$ và $\overrightarrow{j}=\left(1;0\right)$.

D. $\overrightarrow{c}=\left(1;3\right)$ và $\overrightarrow{d}=\left(2;-6\right)$.

Lời giải

+) Xét hai vectơ $\overrightarrow{u}=\left(2;3\right)$ và $\overrightarrow{v}=\left(\frac{1}{2};6\right)$:

Ta có: $\frac{2}{\frac{1}{2}}\ne \frac{3}{6}$ suy ra hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ không cùng phương.

 Do đó A sai.

+) Xét hai vectơ $\overrightarrow{a}=\left(\sqrt{2};6\right)$ và $\overrightarrow{b}=\left(1;3\sqrt{2}\right)$:

Ta có: $\frac{\sqrt{2}}{1}=\frac{6}{3\sqrt{2}}=\sqrt{2}$ suy ra hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$cùng phương.

Do đó B đúng.

+) Xét hai vectơ $\overrightarrow{i}=\left(0;1\right)$ và $\overrightarrow{j}=\left(1;0\right)$:

Đây là hai vectơ đơn vị nên chúng vuông góc với nhau suy ra hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$  không cùng phương.

Do đó C sai.

+) Xét hai vectơ $\overrightarrow{c}=\left(1;3\right)$ và $\overrightarrow{d}=\left(2;-6\right)$:

Ta có: $\frac{1}{2}\ne \frac{3}{-6}$ suy ra hai vectơ $\overrightarrow{c}$ và $\overrightarrow{d}$ không cùng phương.

Do đó D sai.

Vậy ta chọn phương án B.

Bài 4.28 trang 71 Toán 10 Tập 1: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?

A. $\overrightarrow{u}=\left(2;3\right)$ và $\overrightarrow{v}=\left(4;6\right)$.

B. $\overrightarrow{a}=\left(1;-1\right)$ và $\overrightarrow{b}=\left(-1;1\right)$.

C. $\overrightarrow{z}=\left(a;b\right)$ và $\overrightarrow{t}=\left(-b;a\right)$.

D. $\overrightarrow{n}=\left(1;1\right)$ và $\overrightarrow{k}=\left(2;0\right)$.

Lời giải

+) Xét hai vectơ $\overrightarrow{u}=\left(2;3\right)$ và $\overrightarrow{v}=\left(4;6\right)$:

Ta có: $\overrightarrow{u}.\overrightarrow{v}=2.4+3.6=8+18=26\ne 0.$ 

Suy ra hai vectơ $\overrightarrow{u},\overrightarrow{v}$ không vuông góc. Do đó A sai.

+) Xét hai vectơ $\overrightarrow{a}=\left(1;-1\right)$ và $\overrightarrow{b}=\left(-1;1\right)$:

Ta có: $\overrightarrow{a}.\overrightarrow{b}=1.\left(-1\right)+\left(-1\right).1=-1+\left(-1\right)=-2\ne 0.$ 

Suy ra hai vectơ $\overrightarrow{a},\overrightarrow{b}$ không vuông góc với nhau. Do đó B sai.

+) Xét hai vectơ $\overrightarrow{z}=\left(a;b\right)$ và $\overrightarrow{t}=\left(-b;a\right)$:

Ta có: $\overrightarrow{z}.\overrightarrow{t}=a.\left(-b\right)+b.a=-ab+ab=0.$ 

Suy ra hai vectơ $\overrightarrow{z},\overrightarrow{t}$ vuông góc với nhau. Do đó C đúng.

+) Xét hai vectơ $\overrightarrow{n}=\left(1;1\right)$ và $\overrightarrow{k}=\left(2;0\right)$:

Ta có: $\overrightarrow{n}.\overrightarrow{k}=1.2+1.0=2+0=2\ne 0.$ 

Suy ra hai vectơ $\overrightarrow{n},\overrightarrow{k}$ không vuông góc. Do đó D sai.

Vậy ta chọn phương án C.

Bài 4.29 trang 71 Toán 10 Tập 1: Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?

A. $\overrightarrow{a}=\left(1;1\right)$.

B. $\overrightarrow{b}=\left(1;-1\right)$.

C. $\overrightarrow{c}=\left(2;\frac{1}{2}\right)$.

D. $\overrightarrow{d}=\left(\frac{1}{\sqrt{2}};\frac{-1}{\sqrt{2}}\right)$.

Lời giải

+) Xét vectơ $\overrightarrow{a}=\left(1;1\right)\Rightarrow \left|\overrightarrow{a}\right|=\sqrt{1^2+1^2}=\sqrt{2}\ne 1$. Do đó A sai.

+) Xét vectơ $\overrightarrow{b}=\left(1;-1\right)\Rightarrow \left|\overrightarrow{b}\right|=\sqrt{1^2+{\left(-1\right)}^2}=\sqrt{2}\ne 1$. Do đó B sai.

+) Xét vectơ $\overrightarrow{c}=\left(2;\frac{1}{2}\right)\Rightarrow \left|\overrightarrow{c}\right|=\sqrt{2^2+{\left(\frac{1}{2}\right)}^2}=\sqrt{\frac{17}{4}}\ne 1$. Do đó C sai.

+) Xét vectơ $\overrightarrow{d}=\left(\frac{1}{\sqrt{2}};\frac{-1}{\sqrt{2}}\right)\Rightarrow \left|\overrightarrow{d}\right|=\sqrt{{\left(\frac{1}{\sqrt{2}}\right)}^2+{\left(\frac{-1}{\sqrt{2}}\right)}^2}=1$. Do đó D đúng.

Vậy ta chọn phương án D.

Bài 4.30 trang 71 Toán 10 Tập 1: Góc giữa vectơ $\overrightarrow{a}=\left(1;-1\right)$ và vectơ $\overrightarrow{b}=\left(-2;0\right)$ có số đo bằng:

A. 90°.

B. 0°.

C. 135°.

D. 45°.

Lời giải

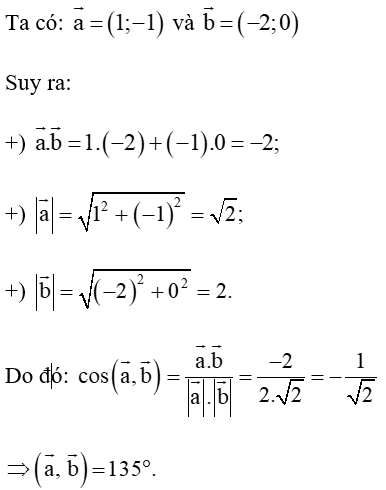
Vậy ta chọn phương án C.

Bài 4.31 trang 71 Toán 10 Tập 1: Khẳng định nào sau đây là đúng?

A. $\left(\overrightarrow{a}.\overrightarrow{b}\right)\overrightarrow{c}=\overrightarrow{a}\left(\overrightarrow{b}.\overrightarrow{c}\right).$

B. ${\left(\overrightarrow{a}.\overrightarrow{b}\right)}^2={\overrightarrow{a}}^2.{\overrightarrow{b}}^2.$

C. $\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\sin \left(\overrightarrow{a},\overrightarrow{b}\right).$

D. $\overrightarrow{a}\left(\overrightarrow{b}-\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{c}.$

Lời giải

+) Xét phương án A:

$\left(\overrightarrow{a}.\overrightarrow{b}\right)\overrightarrow{c}=\left[\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\right]\overrightarrow{c}$;

$\overrightarrow{a}\left(\overrightarrow{b}.\overrightarrow{c}\right)=\overrightarrow{a}\left[\left|\overrightarrow{b}\right|.\left|\overrightarrow{c}\right|.cos\left(\overrightarrow{b},\overrightarrow{c}\right)\right]$.

Suy ra $\left(\overrightarrow{a}.\overrightarrow{b}\right)\overrightarrow{c}\ne \overrightarrow{a}\left(\overrightarrow{b}.\overrightarrow{c}\right).$ Do đó A sai.

+) Xét phương án B:

${\left(\overrightarrow{a}.\overrightarrow{b}\right)}^2={\left[\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\right]}^2={\left|\overrightarrow{a}\right|}^2.{\left|\overrightarrow{b}\right|}^2.co{s}^2\left(\overrightarrow{a},\overrightarrow{b}\right)$

${\overrightarrow{a}}^2.{\overrightarrow{b}}^2={\left|\overrightarrow{a}\right|}^2.{\left|\overrightarrow{b}\right|}^2.$

Suy ra ${\left(\overrightarrow{a}.\overrightarrow{b}\right)}^2={\overrightarrow{a}}^2.{\overrightarrow{b}}^2$ chỉ đúng khi $co{s}^2\left(\overrightarrow{a},\overrightarrow{b}\right)=1$. Do đó B sai.

+) Xét phương án C:

$\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.c\text{os}\left(\overrightarrow{a},\overrightarrow{b}\right)\ne \left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\sin \left(\overrightarrow{a},\overrightarrow{b}\right).$

Do đó C sai.

+)Xét phương án D:

Theo tính chất của tích vô hướng ta có:

 $\overrightarrow{a}\left(\overrightarrow{b}-\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{c}$ (tính chất phân phối đối với phép trừ).

Vậy ta chọn phương án D.

Bài 4.32 trang 71 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?

A. $\left(\overrightarrow{AB},\overrightarrow{BD}\right)=45°.$

B. $\overrightarrow{AC}.\overrightarrow{BC}=a^2.$

C. $\overrightarrow{AC}.\overrightarrow{BD}=a^2\sqrt{2}.$       

D. $\overrightarrow{BA}.\overrightarrow{BD}=-a^2.$

Lời giải

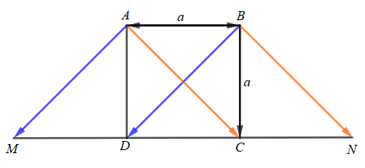
ABCD là hình vuông cạnh a nên AB = BC = CD = DA = a;

Và $BD=AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$ 

Lấy điểm M và N sao cho ABDM, ABNC là các hình bình hành.

+) Vì ABDM là hình bình hành nên $\overrightarrow{BD}=\overrightarrow{AM}$

$\Rightarrow \left(\overrightarrow{AB},\overrightarrow{BD}\right)=\left(\overrightarrow{AB},\overrightarrow{AM}\right)=\widehat{BAM}=90°+45°=135°.$ 

Do đó A sai.

+) Vì ABNC là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{BN}$

$\Rightarrow \left(\overrightarrow{AC},\overrightarrow{BC}\right)=\left(\overrightarrow{BN},\overrightarrow{BC}\right)=\widehat{CBN}=45°$

$\Rightarrow \overrightarrow{AC}.\overrightarrow{BC}=AC.BC.cos\widehat{CBF}=a\sqrt{2}.a.c{\text{os45}}^0=a^2.$

Do đó B đúng.

+) Ta có $AC\perp BD\Rightarrow \overrightarrow{AC}\perp \overrightarrow{BD}\Rightarrow \overrightarrow{AC}.\overrightarrow{BD}=0$.

Do đó C sai.

+) Ta có:

$$\begin{gathered} \overrightarrow{BA}.\overrightarrow{BD}=BA.BD.\cos \left(\overrightarrow{BA},\overrightarrow{BD}\right) \\ =BA.BD.\cos \widehat{ABD}=a.a\sqrt{2}.c{\text{os45}}^0=a^2. \end{gathered}$$ 

Do đó D sai.

B. Tự luận

Bài 4.33 trang 71 Toán 10 Tập 1: Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.

a) Tìm mối liên hệ giữa hai vectơ $\overrightarrow{MB}$ và $\overrightarrow{MC}$.

b) Biểu thị vectơ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}.$

Lời giải

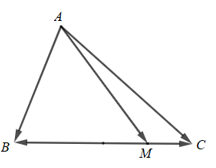
a) Vì điểm M nằm trên cạnh BC nên hai vectơ $\overrightarrow{MB}$ và $\overrightarrow{MC}$ là hai vectơ ngược hướng.

Lại có MB = 3MC nên $\overrightarrow{MB}=-3\overrightarrow{MC}$.

Vậy $\overrightarrow{MB}=-3\overrightarrow{MC}.$

b) Theo câu a: $\overrightarrow{MB}=-3\overrightarrow{MC}\Rightarrow \overrightarrow{MB}=3\overrightarrow{CM}=\frac{3}{4}\overrightarrow{CB}=-\frac{3}{4}\overrightarrow{BC}.$

Ta có: $\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}-\overrightarrow{MB}$

$=\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}=\overrightarrow{AB}+\frac{3}{4}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)$  (quy tắc ba điểm)

$=\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}-\frac{3}{4}\overrightarrow{AB}=\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$

Vậy $\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\widehat{AC}$.

Bài 4.34 trang 72 Toán 10 Tập 1: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

$\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$

Lời giải

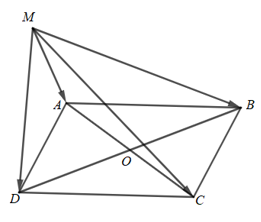
Gọi O là giao điểm của AC và BD.

Suy ra O là trung điểm của AC và BD.

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$ và $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$

Ta có:

+) 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OC} \\ =2\overrightarrow{MO}+\left(\overrightarrow{OA}+\overrightarrow{OC}\right)=2\overrightarrow{MO} \end{gathered}$$

(Vì $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$)

+) 

$$\begin{gathered} \overrightarrow{MB}+\overrightarrow{MD}=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD} \\ =2\overrightarrow{MO}+\left(\overrightarrow{OB}+\overrightarrow{OD}\right)=2\overrightarrow{MO} \end{gathered}$$

 (Vì $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$)

Suy ra $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}.$

Vậy $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}.$

Bài 4.35 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(‒2; 5) và C(‒5; 2).

a) Tìm tọa độ của các vectơ $\overrightarrow{BA}$ và $\overrightarrow{BC}.$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Lời giải

a) Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: $\overrightarrow{BA}=\left(4;-4\right)$ và $\overrightarrow{BC}=\left(-3;-3\right).$

b) Ta có: 

$\overrightarrow{BA}.\overrightarrow{BC}=4.\left(-3\right)+\left(-4\right).\left(-3\right)=-12+12=0$

$\Rightarrow \overrightarrow{BA}\perp \overrightarrow{BC}$

$\Rightarrow BA\perp BC$

$\Rightarrow \Delta ABC$ vuông tại B.

Do $\overrightarrow{BA}=\left(4;-4\right)\Rightarrow BA=\sqrt{4^2+{\left(-4\right)}^2}=4\sqrt{2}$;

$\overrightarrow{BC}=\left(-3;-3\right)\Rightarrow BC=\sqrt{{\left(-3\right)}^2+{\left(-3\right)}^2}=3\sqrt{2}$.

Với A(2; 1) và C(‒5; 2) ta có:

$\overrightarrow{AC}=\left(-7;1\right)\Rightarrow AC=\sqrt{{\left(-7\right)}^2+1^2}=\sqrt{50}=5\sqrt{2}$ 

Diện tích tam giác vuông ABC là:

$S_{\Delta ABC}=\frac{1}{2}.AB.BC=\frac{1}{2}.4\sqrt{2}.3\sqrt{2}=12$ (đơn vị diện tích)

Chu vi tam giác ABC là:

AB + BC + AC = $4\sqrt{2}+3\sqrt{2}+5\sqrt{2}=12\sqrt{2}$ (đơn vị độ dài)

c)  Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có tọa độ trọng tâm G của tam giác ABC là:

$\left\{\begin{array}{l}{x}_G=\frac{2+\left(-2\right)+\left(-5\right)}{3}=\frac{-5}{3}\\ y_G=\frac{1+5+2}{3}=\frac{8}{3}\end{array}\right.\Rightarrow G\left(\frac{-5}{3};\frac{8}{3}\right)$

Vậy tọa độ trọng tâm của tam giác ABC là: $G\left(\frac{-5}{3};\frac{8}{3}\right).$

d)

Để tứ giác BCAD là hình bình hành thì $\overrightarrow{AC}=\overrightarrow{DB}$

Giả sử D(x; y) là điểm cần tìm.

Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: $\overrightarrow{AC}=\left(-7;1\right)$ và $\overrightarrow{DB}=\left(-2-x;5-y\right)$ 

Do đó $\overrightarrow{AC}=\overrightarrow{DB}$

$\iff \left\{\begin{array}{l}-2-x=-7\\ 5-y=1\end{array}\right.\iff \left\{\begin{array}{l}x=5\\ y=4\end{array}\right.\Rightarrow D\left(5;4\right)$.

Vậy với D(5;4) thì tứ giác BCAD là một hình bình hành.

Bài 4.36 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(1; 2), B(3; 4), C(‒1; ‒2) và D(6; 5).

a) Tìm tọa độ của các vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$.

b) Hãy giải thích tại sao các vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương.

c) Giả sử E là điểm có tọa độ (a; 1). Tìm a để vectơ $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương.

d) Với a tìm được, hãy biểu thị vectơ $\overrightarrow{AE}$ theo các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

Lời giải

a) Với A(1; 2), B(3; 4), C(‒1; ‒2) và D(6; 5) ta có: $\overrightarrow{AB}=\left(2;2\right)$ và $\overrightarrow{CD}=\left(7;7\right)$.

b) Xét hai vectơ $\overrightarrow{AB}=\left(2;2\right)$ và $\overrightarrow{CD}=\left(7;7\right)$:

Ta có: $\frac{7}{2}=\frac{7}{2}$ nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương.

Vậy hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương.

c) Với A(1; 2), B(3; 4), C(‒1; ‒2) và E(a; 1) ta có: $\overrightarrow{AC}=\left(-2;-4\right)$ và $\overrightarrow{BE}=\left(a-3;-3\right)$

Hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương khi và chỉ khi $\frac{a-3}{-2}=\frac{-3}{-4}$ 

$\iff$ (‒ 4).(a – 3) = (‒3). (‒2)

$\iff$ ‒ 4a + 12 = 6

$\iff$ 4a = 6

$\iff a=\frac{3}{2}.$

Vậy $a=\frac{3}{2}$ thì hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương.

d) Với $a=\frac{3}{2}\Rightarrow E\left(\frac{3}{2};1\right)$

Với A(1; 2) và $E\left(\frac{3}{2};1\right)$ $\Rightarrow \overrightarrow{AE}=\left(\frac{1}{2};-1\right)$ 

Ta có: $\overrightarrow{AB}=\left(2;2\right)$ và $\overrightarrow{AC}=\left(-2;-4\right)$

Tồn tại hai số thực m và n thỏa mãn: $\overrightarrow{AE}=m\overrightarrow{AB}+n\overrightarrow{AC}$

$\iff \left\{\begin{array}{l}\frac{1}{2}=m.2+n.\left(-2\right)\\ -1=m.2+n.\left(-4\right)\end{array}\right.\iff \left\{\begin{array}{l}2m-2n=\frac{1}{2}\\ 2m-4n=-1\end{array}\right.\iff \left\{\begin{array}{l}m=1\\ n=\frac{3}{4}\end{array}\right.$

$\Rightarrow \overrightarrow{AE}=\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$

Vậy $\overrightarrow{AE}=\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$.

Bài 4.37 trang 72 Toán 10 Tập 1: Cho vectơ $\overrightarrow{a}\ne \overrightarrow{0}.$ Chứng minh rằng $\frac{1}{\left|\overrightarrow{a}\right|}\overrightarrow{a}$ (hay còn được viết là $\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$) là một vectơ đơn vị, cùng hướng với vectơ $\overrightarrow{a}$.

Lời giải

Ta thấy $\frac{1}{\left|\overrightarrow{a}\right|}>0\left(\overrightarrow{a}\ne \overrightarrow{0}\right)$ nên $\frac{1}{\left|\overrightarrow{a}\right|}\overrightarrow{a}$ là vectơ cùng hướng với vectơ $\overrightarrow{a}.$

Độ dài của vectơ $\frac{1}{\left|\overrightarrow{a}\right|}\overrightarrow{a}$ là: $\left|\frac{1}{\left|\overrightarrow{a}\right|}\overrightarrow{a}\right|=\left|\frac{1}{\left|\overrightarrow{a}\right|}\right|.\left|\overrightarrow{a}\right|=\frac{1}{\left|\overrightarrow{a}\right|}.\left|\overrightarrow{a}\right|=1$

Vậy vectơ $\frac{1}{\left|\overrightarrow{a}\right|}\overrightarrow{a}$ (hay còn được viết là $\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$) là một vectơ đơn vị, cùng hướng với vectơ $\overrightarrow{a}$.

Bài 4.38 trang 72 Toán 10 Tập 1: Cho ba vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{u}$ với $\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1$ và $\overrightarrow{a}\perp \overrightarrow{b}$. Xét một hệ trục Oxy với các vectơ đơn vị $\overrightarrow{i}=\overrightarrow{a},\overrightarrow{j}=\overrightarrow{b}$. Chứng minh rằng:

a) Vectơ $\overrightarrow{u}$ có tọa độ là $\left(\overrightarrow{u}.\overrightarrow{a};\overrightarrow{u}.\overrightarrow{b}\right).$  

b) $\overrightarrow{u}=\left(\overrightarrow{u}.\overrightarrow{a}\right).\overrightarrow{a}+\left(\overrightarrow{u}.\overrightarrow{b}\right).\overrightarrow{b}.$

Lời giải

Bài 4.39 trang 72 Toán 10 Tập 1: Trên sông, một ca nô chuyển động thẳng đều theo hướng S15°E (xem chú thích ở Bài 3.8, trang 42) với vận tốc có độ lớn bằng 20km/h. Tính vận tốc riêng của ca nô, biết rằng nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.

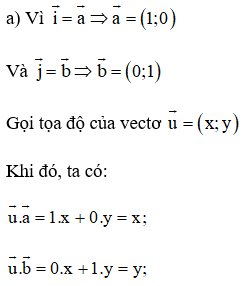
Lời giải

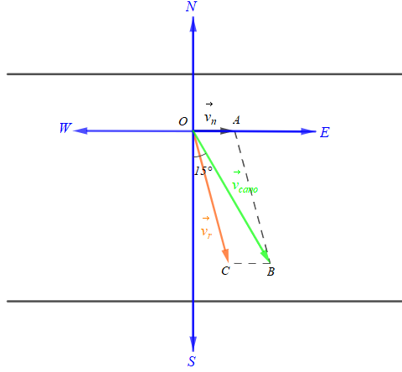
Ta mô tả bài toán bằng hình vẽ trên, trong đó:

$\overrightarrow{OE}$ là hướng đông, $\overrightarrow{\text{OS}}$ là hướng nam, $\overrightarrow{OW}$ là hướng tây, $\overrightarrow{ON}$ là hướng bắc;

$\overrightarrow{OA}$ biểu diễn vectơ vận tốc của dòng nước ${\overrightarrow{v}}_n$ và $OA=\left|{\overrightarrow{v}}_n\right|=3$;

$\overrightarrow{OB}$ là hướng S15°E biểu diễn vectơ vận tốc chuyển động của ca nô ${\overrightarrow{v}}_{cano}$ tạo với $\overrightarrow{OS}$ một góc 15° và $OB=\left|{\overrightarrow{v}}_{cano}\right|=20$;

Lấy điểm C sao cho OABC là hình bình hành. Khi đó $\overrightarrow{OC}$ biểu diễn vectơ vận tốc riêng ${\overrightarrow{v}}_r$của ca nô.

Vì $\overrightarrow{OB}$ tạo với $\overrightarrow{OS}$ một góc 15° nên $\overrightarrow{OB}$ tạo với $\overrightarrow{OA}$ một góc là 90° ‒ 15° = 75° tức là $\widehat{AOB}=75°$ 

Xét tam giác OAB có: AB² = OA² + OB² – 2.OA.OB.cos$\widehat{AOB}$ 

$\Rightarrow$ AB² = 3² + 20² – 2.3.20.cos75°

$\Rightarrow$ AB ≈ 19,44

Vì OABC là hình bình hành nên OC = AB ≈ 19,44 (tính chất hình bình hành)

Suy ra $\left|{\overrightarrow{v}}_r\right|=\left|\overrightarrow{OC}\right|=OC\approx 19,44$ (km/h)

Vậy vận tốc riêng của ca nô khoảng 19,44 km/h.