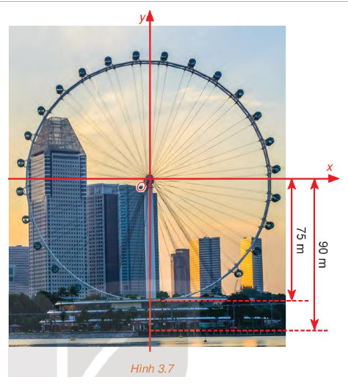
Giải Toán 10 Kết nối tri thức Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Hamchoi.vn trân trọng giới thiệu: lời giải bài tập Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 5. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Bài giảng Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Mở đầu
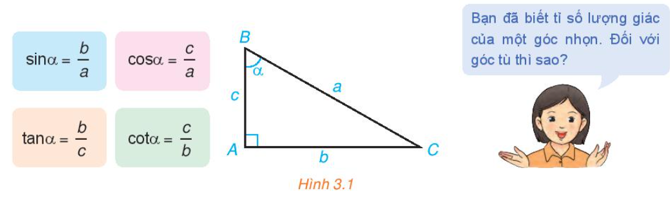
Mở đầu trang 33 Toán 10 Tập 1: Bạn đã biết tỉ số lượng giác của 1 góc nhọn. Đối với góc tù thì sao?
Lời giải:
Sau bài học này ta sẽ trả lời được:
Với góc α cho trước, 0o < α < 180o.
Trên nửa đường tròn đơn vị, vẽ điểm M(x0; y0) sao cho .
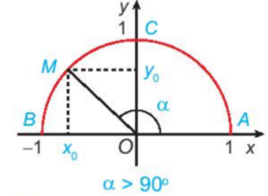
Khi đó: sinα = y0; cosα = x0;
tanα = (x0 ≠ 0); cotα = (y0 ≠ 0).
1. Gía trị lượng giác của 1 góc
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
b) Khi 0o < α < 90o, nêu mối quan hệ giữa cos α, sin α với hoành độ và tung độ của điểm M.
Lời giải:
a) Gọi điểm A có tọa độ A(1; 0).
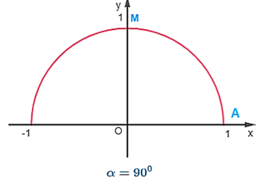
• α = 90o hay . Khi đó, điểm M có tọa độ M(0;1).
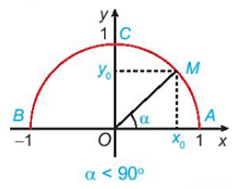
• α < 90o hay .
Do đó, điểm M(x0; y0) nằm trên cung tròn (không tính điểm C) thỏa mãn 0 < x0 ≤ 1, 0 ≤ y0 < 1.
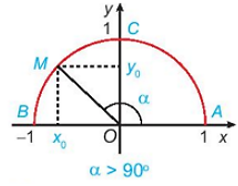
• α > 90o hay .
Do đó, điểm M(x0; y0) nằm trên cung tròn (không tính điểm C) thỏa mãn −1 ≤ x0 < 0, 0 ≤ y0 < 1.
b) Khi 0o < α < 90o
Kẻ MH ^ Ox, MK ^ Oy (H Î Ox, H Î Oy). Khi đó .
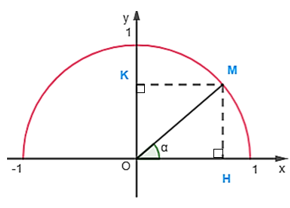
Gọi điểm M có tọa độ M(x0; y0).
Xét tứ giác MKOH có:
(Ox ^ Oy)
(MH ^ Ox)
(MK ^ Oy)
Do đó tứ giác MKOH là hình chữ nhật.
Suy ra OH = |x0| = x0; MH = OK = |y0| = y0.
Ta có OM = 1 (bán kính đường tròn đơn vị).
Xét ∆MHO vuông tại H, ta có:
Hay sin α = y0.
Ta lại có: .
Hay cos α = x0.
Vậy cos α là hoành độ của điểm M và sin α là tung độ của điểm M.
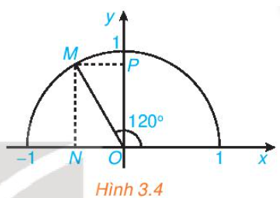
Luyện tập 1 trang 35 Toán 10 Tập 1: Tìm các giá trị lượng giác của góc 120o (H.3.4).
Lời giải:
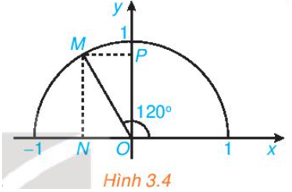
Điểm M nằm trên nửa đường tròn đơn vị sao cho .
Hai điểm N, P tương ứng là hình chiếu vuông của M lên hai trục Ox, Oy.
Ta có: OM = 1 (bán kính đường tròn đơn vị).
Ta có .
.
Xét tam giác vuông MON, có:
+
.
+
.
Ta có điểm M nằm bên trái trục Oy (vì là góc tù).
Suy ra điểm M có tọa độ là M.
Do đó theo định nghĩa ta có: sin120° = , cos120° = .
Suy ra
+
.
+
.
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Lời giải:
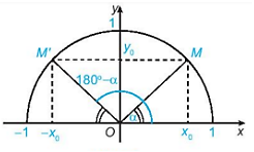
Hai điểm M và M’ đối xứng với nhau qua trục Oy.
Tọa độ của hai điểm M và M’ là: M(x0; y0), M’(–x0; y0).
Ta có: .
Khi đó:
∙ sin α = y0, cos α = x0.
∙ sin (180o – α) = y0, cos (180o – α) = –x0 hay x0 = – cos (180o – α).
Do đó: sin α = sin (180o – α) (= y0), cos α = – cos (180o – α) (= x0).
Vậy sin α = sin (180o – α), cos α = – cos (180o – α).
Lời giải:
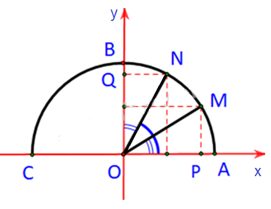
Ta có:
Dễ thấy: .
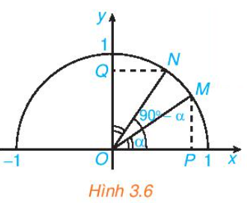
Xét ∆NOQ và ∆MOP có:
OM = ON = 1 (bán kính đường tròn đơn vị).
.
Do đó ΔNOQ = ΔMOP (cạnh huyền – góc nhọn)
Suy ra OP = OQ (hai cạnh tương ứng)
Ta có: OP = cos α, OQ = sin (90o – α).
Do đó: cos α = sin (90o − α).
Lời giải:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí thấp nhất của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A, A’, B, H (như hình vẽ).
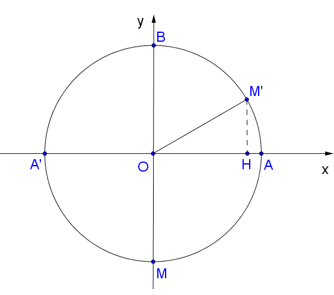
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng chu vi đường tròn.
Sau 15 phút, cabin di chuyển từ điểm M đến điểm B, đi được chu vi đường tròn.
Trong 5 phút tiếp theo, cabin đi chuyển từ điểm B đến điểm M’ tương ứng chu vi đường tròn hay cung tròn .
Do đó:
Ta có (m).
Do đó, độ cao của người đó là:
37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.
Bài tập
a) (2sin 30o + cos 135o – 3tan 150o) . (cos 180o – cot 60o);
b) sin2 90o + cos2 120o + cos2 0o – tan2 60o + cot2 135o;
c) cos 60o . sin 30o + cos2 30o.
Chú ý: sin2 α = (sin α)2 , cos2 α = (cos α)2 , tan2 α = (tan α)2 , cot2 α = (cot α)2.
Lời giải:
a) Đặt A = (2sin 30o + cos 135o – 3tan 150o) . (cos 180o – cot 60o).
Ta có: cos 135o = – cos 45o; cos 180o = – cos 0o; tan 150o = – tan30o; cot60° = tan 30°.
A = (2sin30o – cos 45o + 3tan 30o) . (– cos 0o – tan 30o).
Sử dụng bảng lượng giác của một số góc đặc biệt, ta có:
; ; ; cos 0o = 1.
Do đó
.
b) Đặt B = sin2 90o + cos2 120o + cos2 0o – tan2 60o + cot2 135o.
Ta có: cos 120o = – cos 60o; cot 135o = – cot 45o
cos2 120o = cos2 60o; cot2 135o = cot2 45o
Khi đó B = sin2 90o + cos2 60o + cos2 0o – tan2 60o + cot2 45o.
Sử dụng bảng lượng giác của một số góc đặc biệt, ta có:
cos 0o = 1; cot 45o = 1; ; ; sin 90o = 1.
Do đó
c) Đặt C = cos 60o . sin 30o + cos2 30o
Sử dụng bảng lượng giác của một số góc đặc biệt, ta có:
; ; .
Do đó
.
Bài 3.2 trang 37 Toán 10 Tập 1: Đơn giản các biểu thức sau:
a) sin 100o + sin 80o + cos 16o + cos 164o;
b) 2sin (180o – α) . cot α – cos (180o – α) . tan α . cot (180o – α) với 0o < α < 90o.
Lời giải:
a) Ta có: sin 100o = sin (180o – 100o) = sin 80o;
cos 164o = cos (180o – 16o) = – cos 16o.
Do đó sin 100o + sin 80o + cos 16o + cos 164o
= sin 80o + sin 80o + cos 16o – cos 16o
= 2sin 80o.
b) Với 0o < α < 90o, ta có:
sin (180o – α) = sin α; cos (180o – α) = – cos α;
tan (180o – α) = – tan α; cot (180o – α) = – cot α.
Khi đó,
2sin (180o – α) . cot α – cos (180o – α) . tan α . cot (180o – α)
= 2sin α . cot α – (– cos α) . tan α . (– cot α)
= 2sin α . cot α – cos α . tan α . cot α
= 2sin α . – cos α .
= 2cos α – cos α = cos α.
Bài 3.3 trang 37 Toán 10 Tập 1: Chứng minh các hệ thức sau:
Lời giải:
a)
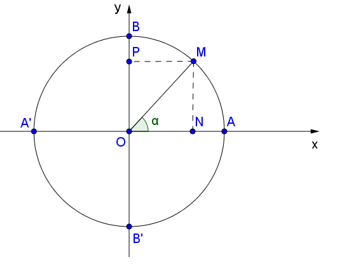
Gọi M(x; y) là điểm trên đường tròn đơn vị sao cho .
Ta có: OM = 1 (bán kính đường tròn đơn vị).
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: (1)
Mà (2)
Từ (1) và (2) suy ra: sin2 α + cos2 α = ON2 + MN2 = OM2 = 1 (do ∆OMN vuông tại N).
Do đó sin2 α + cos2 α = 1 (đpcm).
b) Ta có: (α ≠ 90o)
.
Mà theo câu a) ta có: sin2 α + cos2 α = 1 với mọi góc α.
(đpcm)
c) Ta có: (0o < α < 180o)
.
Mà theo câu a) ta có: sin2 α + cos2 α = 1 với mọi góc α.
(đpcm).
Bài 3.4 trang 37 Toán 10 Tập 1: Cho góc α (0o < α < 180o) thỏa mãn tan α = 3.
Lời giải:
Ta có: (α ≠ 90o)
.
Vì 0o < α < 180o nên sin α > 0.
Mà tan α = 3 > 0 cos α > 0 .
Lại có: sin α = cos α . tan α = .
Do đó
.
Vậy với α (0o < α < 180o) thỏa mãn tan α = 3 thì .