Giải bài tập Toán 10 Bài tập cuối chương 7

A.  Trắc nghiệm

Bài 7.26 trang 58 Toán 10 Tập 2:

Phương trình nào sau đây là phương trình tham số của đường thẳng?

A. 2x – y + 1 = 0;

B. $\left\{\begin{array}{l}x=2t\\ y=t\end{array}\right.$;

C. x² + y² = 1;

D. y = 2x + 3.

Lời giải 

Ta thấy 2x – y + 1 = 0; y = 2x + 3 là phương trình tổng quát của đường thẳng. Do đó A, D sai.

Ta thấy x² + y² = 1 là phương trình đường tròn. Do đó C sai.

Phương trình $\left\{\begin{array}{l}x=2t\\ y=t\end{array}\right.$ là phương trình tham số của đường thẳng. Do đó B đúng.

Vậy chọn đáp án B.

Bài 7.27 trang 58 Toán 10 Tập 2:

Phương trình nào sau đây là phương trình tổng quát của đường thẳng?

A. –x – 2y + 3 = 0;

B. $\left\{\begin{array}{l}x=2+t\\ y=3-t\end{array}\right.$;

C. y² = 2x;

D. $\frac{x^2}{10}+\frac{y^2}{6}=1$.

Lời giải 

Ta có:

$\left\{\begin{array}{l}x=2+t\\ y=3-t\end{array}\right.$ là phương trình tham số của đường thẳng. Do đó B sai.

y² = 2x là phương trình chính tắc của parabol. Do đó C sai.

$\frac{x^2}{10}+\frac{y^2}{6}=1$ là phương trình chính tắc của elip. Do đó D sai.

–x – 2y + 3 = 0 là phương trình tổng quát của đường thẳng. Do đó A đúng.

Vậy chọn đáp án A.

Bài 7.28 trang 58 Toán 10 Tập 2:

Phương trình nào sau đây là phương trình đường tròn ?

A. x² – y² = 1;

B. (x – 2)² – (y – 2)² = 1;

C. x² + y² = 2;

D. y² = 8x.

Lời giải 

 x² – y² =  1 có hệ hệ số của y² là – 1 ≠ 1 nên phương trình x² – y² =  1 không là phương trình đường tròn. Do đó A sai.

(x – 2)² – (y – 2)² = 1 không thoả mãn dạng của phương trình đường tròn (x – a)² + (y – b)² = R². Do đó B sai.

y² = 8x là phương trình chính tắc của parabol. Do đó D sai.

x² + y² = 2 là phương trình đường tròn có tâm I(0;0) và R = $\sqrt{2}$. Do đó C đúng.

Vậy chọn đáp án C.

Bài 7.29 trang 58 Toán 10 Tập 2:

Phương trình nào sau đây là phương trình chính tắc của đường elip?

A. $\frac{x^2}{9}+\frac{y^2}{9}=1$;

B. $\frac{x^2}{1}+\frac{y^2}{6}=1$;

C. $\frac{x^2}{4}-\frac{y^2}{1}=1$;

D. $\frac{x^2}{2}+\frac{y^2}{1}=1$

Lời giải 

$\frac{x^2}{9}+\frac{y^2}{9}=1$ có a =  b = 3 không thoả mãn điều kiện a > b > 0 nên $\frac{x^2}{9}+\frac{y^2}{9}=1$ không là phương trình chính tắc của đường elip. Do đó A sai

$\frac{x^2}{1}+\frac{y^2}{6}=1$ có a = 1; b = $\sqrt{6}$mà a < b không thoả mãn điều kiện a > b > 0 nên $\frac{x^2}{1}+\frac{y^2}{6}=1$ không là phương trình chính tắc của đường elip. Do đó B sai

$\frac{x^2}{4}-\frac{y^2}{1}=1$là phương trình hypebol. Do đó C sai

$\frac{x^2}{2}+\frac{y^2}{1}=1$ là phương trình elip vì a = $\sqrt{2}$; b = 1 nên a > b > 0. Do đó D đúng.

Vậy chọn đáp án D.

Bài 7.30 trang 58 Toán 10 Tập 2:

Phương trình nào sau đây là phương trình chính tắc của đường hypebol?

A. $\frac{x^2}{3}-\frac{y^2}{2}=-1$

B. $\frac{x^2}{1}-\frac{y^2}{6}=1$

C. $\frac{x^2}{6}+\frac{y^2}{1}=1$

D. $\frac{x^2}{2}+\frac{y^2}{1}=-1$

Lời giải 

$\frac{x^2}{3}-\frac{y^2}{2}=-1$ không có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ nên không là phương trình chính tắc của đường hypebol. Do đó A sai

$\frac{x^2}{6}+\frac{y^2}{1}=1$là phương trình elip. Do đó C sai

$\frac{x^2}{2}+\frac{y^2}{1}=-1$ không có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ nên không là phương trình chính tắc của đường hypebol. Do đó D sai

Đáp án : B. $\frac{x^2}{1}-\frac{y^2}{6}=1$

Vì a = 1; b = $\sqrt{6}$⇒ c = $\sqrt{1+6}=\sqrt{7}$

 Ta có : 1 < $\sqrt{7}$ hay a <  c nên theo định nghĩa hypebol ta có: $\frac{x^2}{1}-\frac{y^2}{6}=1$ là phương trình chính tắc của đường hypebol.

Vậy chọn đáp án B.

Bài 7.31 trang 58 Toán 10 Tập 2:

Phương trình nào sau đây là phương trình chính tắc của đường parabol?

A. x² = 4y

B. x² = -6y

C. y² = 4x

D. y² = -4x

Lời giải 

Phương trình chính tắc của parabol có dạng y² = 2px (p > 0).

Ta thấy chỉ có đáp án C có phương trình dạng trên và thỏa mãn p = 2 > 0 ( thoả mãn điều kiên về phương trình chính tắc của parabol).

Vậy đáp án cần chọn là C.

B. Bài tập

Bài 7.32 trang 58 Toán 10 Tập 2:

Trong mặt phẳng toạ độ, cho A(1; −1), B(3; 5); C(−2; 4). Tính diện tích tam giác ABC

Lời giải 

Ta có: $\overrightarrow{CB}$= (5; 1) ⇒ BC = $\sqrt{5^2+1^2}$ = $\sqrt{26}$

Ta lại có $\overrightarrow{CB}$= (5; 1) là vectơ chỉ phương của đường thẳng BC nên vectơ pháp tuyến của BC là $\overrightarrow{n}$(−1; 5).

Đường thẳng BC đi qua điểm B(3; 5) và có vectơ pháp tuyến $\overrightarrow{n}$(−1; 5), có phương trình là:

−1(x – 3) + 5(y − 5) = 0 ⇒ −x + 5y – 22 = 0

d(A; BC) = $\frac{\left|-1+5.(-1)–22\right|}{\sqrt{{(-1)}^2+5^2}}$= $\frac{14\sqrt{26}}{13}$.

Khi đó diện tích tam giác ABC là: S = $\frac{1}{2}$. d(A; BC). BC = $\frac{1}{2}$.$\frac{14\sqrt{26}}{13}$.$\sqrt{26}$ =14 (đvdt).

Vậy diện tích tam giác ABC là 14 đvdt.

Bài 7.33 trang 58 Toán 10 Tập 2:

Trong mặt phẳng toạ độ, cho hai điểm A(−1; 0) và B(3; 1)

a) Viết phương trình đường tròn tâm A và đi qua B

b) Viết phương trình tổng quát của đường thẳng AB

c) Viết phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB

Lời giải

a) Phương trình đường tròn tâm A có dạng : (x + 1)² + y² = R² (với R là bán kính của đường tròn tâm A).

Vì đường tròn đi qua điểm B(3; 1) nên (3 + 1)² + 1² = R² ⇒ R² = 17

Vậy phương trình đường tròn là: (x + 1)² + y² = 17

b) Đường thẳng AB có vectơ chỉ phương $\overrightarrow{AB}$= (4; 1) nên vectơ pháp tuyến là $\overrightarrow{n}$(−1; 4).

Vậy phương trình đường thẳng AB là: −1(x + 1) + 4(y – 0) = 0 hay –x + 4y −1 = 0.

c) Vì đường tròn tâm O và tiếp xúc với đường thẳng AB nên

R = d(O; AB) = $\frac{\left|-0+4.0-1\right|}{\sqrt{{(-1)}^2+4^2}}$= $\frac{1}{\sqrt{17}}$

Vậy phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB là:

(x – 0)² + (y – 0)² = $\frac{1}{17}$ hay x ² + y ² = $\frac{1}{17}$.

Bài 7.34 trang 58 Toán 10 Tập 2:

Cho đường tròn (C) có phương trình x² + y² – 4x + 6y – 12 = 0

a) Tìm toạ độ tâm I và bán kính R của (C).

b) Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.

Lời giải 

a) Với phương trình x² + y² – 4x + 6y – 12 = 0 hay x² + y² – 2.2x – 2.( –3) y + (– 12) = 0.

⇒ a = 2; b = –3; c = –12

Khi đó, tâm I(2; –3) và bán kinh R = $\sqrt{a^2+b^2-c}=\sqrt{2^2+{(-3)}^2+12}=5$

b) Thay tọa độ điểm M vào phương trình đường tròn (C) ta được:

5² + 1² – 4.5 + 6.1 – 12 = 0

⇔ 25 + 1 – 20 + 6 – 12 = 0

⇔ 0 = 0 (luôn đúng)

⇒  M(5; 1) ∈ (C).

Ta có: $\overrightarrow{IM}$= (3; 4)

Vì d là phương trình tiếp tuyến của (C) tại M nên IM ⊥ d, do đó đường thẳng d nhận $\overrightarrow{IM}$= (3; 4) làm vectơ pháp tuyến.

Phương trình tiếp tuyến d của (C) tại M(5; 1) có vectơ pháp tuyến $\overrightarrow{IM}$= (3; 4) là:

3(x – 5) + 4(y – 1) = 0 ⇔ 3x + 4y – 19 = 0.

Bài 7.35 trang 59 Toán 10 Tập 2:

Cho elip (E) : $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a > b > 0)

a) Tìm các giao điểm A₁, A₂ của (E) với trục hoành và các giao điểm B₁, B₂ của (E) với trục tung. Tính A₁A₂; B₁B₂

b) Xét một điểm bất kì M(x₀; y₀) thuộc (E).

Chứng minh rằng: b²  ≤ $x_0^2+y_0^2$ ≤  a² và b ≤ OM ≤ a

Chú ý: A₁A₂; B₁B₂ tương ứng được là trục lớn, trục nhỏ của elip (E) và tương ứng có độ dài là 2a, 2b              

Lời giải 

a) Giao điểm của (E) với trục hoành có y = 0 nên $\frac{x^2}{a^2}+\frac{0^2}{b^2}=1$ ⇒ x²  = a² ⇒ x = ± a

Do đó, giao điểm của (E) với trục hoành lần lượt là: A₁(−a; 0),  A₂(a; 0).

⇒ $\overrightarrow{A_1{A}_2}\left(2a;0\right)$ ⇒ A₁A₂ = $\sqrt{{\left(2a\right)}^2+0^2}$= 2a.

Giao điểm của (E) với trục tung có x = 0 nên $\frac{0^2}{a^2}+\frac{y^2}{b^2}=1$ ⇒ y²  = b² ⇒ y = ± b

Do đó, giao điểm của (E) với trục tung lần lượt là: B₁(0; −b),  B₂(0; b).

⇒ $\overrightarrow{B_1{B}_2}\left(0;2b\right)$ ⇒ B₁B₂ = $\sqrt{0^2+{\left(2b\right)}^2}$= 2b.

Vậy A₁(−a; 0),  A₂(a; 0), B₁(0; −b),  B₂(0; b), A₁A₂ = 2a, B₁B₂ = 2b.

b) Vì M(x₀; y₀) thuộc (E) nên $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$

Vì a > b > 0 nên $\frac{x_0^2}{a^2}\le \frac{x_0^2}{b^2}$ (Dấu “=” xảy ra khi x₀ = 0)

⇔ $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}\le \frac{x_0^2}{b^2}+\frac{y_0^2}{b^2}$ hay $1\le \frac{x_0^2}{b^2}+\frac{y_0^2}{b^2}=\frac{x_0^2+y_0^2}{b^2}$ 

⇒  b²  ≤ $x_0^2+y_0^2$ (1)

Tương tự ta có: $\frac{y_0^2}{a^2}\le \frac{y_0^2}{b^2}$ (Dấu “=” xảy ra khi y₀ = 0)

⇔$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}\ge \frac{x_0^2}{a^2}+\frac{y_0^2}{a^2}$ hay $1\ge \frac{x_0^2}{a^2}+\frac{y_0^2}{a^2}$ ⇒ $x_0^2+y_0^2$ ≤ a² (2)

Từ (1) và (2) suy ra: b²  ≤ $x_0^2+y_0^2$≤  a² (đpcm)

Mặt khác ta có: $\overrightarrow{OM}$= (x₀; y₀) ⟹ OM = $\sqrt{x_0^2+y_0^2}$

Mà b²  ≤ $x_0^2+y_0^2$≤  a² ⇒  b ≤ $\sqrt{x_0^2+y_0^2}$ ≤  a hay b ≤ OM ≤ a (đpcm).

Bài 7.36 trang 59 Toán 10 Tập 2:

Cho hypebol có phương trình : $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

a) Tìm các giao điểm A₁, A₂ của hypebol với trục hoành (hoành độ của A₁ nhỏ hơn của A₂).

b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì x ≤ –a, nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì x ≥ a.

c) Tìm các điểm M₁, M₂ tương ứng thuộc các nhánh bên trái, bên phải trục tung của hyperbol để M₁M₂ nhỏ nhất.

Lời giải 

a) Giao điểm của (H) với trục hoành có y = 0 nên $\frac{x^2}{a^2}-\frac{0^2}{b^2}=1$ ⇒ x²  = a² ⇒ x = ± a;

Hơn nữa hoành độ A₁ nhỏ hơn hoành độ A₂ nên ta có: A₁(−a; 0),  A₂(a; 0).

Vậy tọa độ giao điểm của hypebol với trục hoành lần lượt là A₁(−a; 0),  A₂(a; 0).

b) Ta có: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 

⇔ $\frac{x^2}{a^2}=1+\frac{y^2}{b^2}$ 

Mà $\frac{y^2}{b^2}$≥ 0 nên $\frac{x^2}{a^2}\ge 1$ hay x² ≥ a²  

⇔ |x| ≥ |a|

⇔ x ≥ a hoặc x ≤ - a .

Vậy điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì x ≤ 0 nên x ≤ –a, nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì x ≥ 0 nên x ≥ a.

b) Gọi toạ độ điểm M₁(x_1;y₁),  M₂(x_2;y₂), tương ứng thuộc các nhánh bên trái, bên phải trục tung của hypebol. Khi đó x₁ ≤ – a và x₂ ≥ a.

Ta có:

$\overrightarrow{M_1{M}_2}\left(x_2-x_1;y_2-y_1\right)$ ⇒ M₁M₂ = $\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$;

A₁A₂ = $\sqrt{{(a-(-a\left)\right)}^2+{(0-0)}^2}$ = 2a.

Vì x₁ < 0 và x₂ > 0 nên x₂ – x₁ = $\left|x_2\right|$+$\left|x_1\right|$ (1)

Mặt khác ta có: x₁ ≤ –a  và x₂  ≥  a ⇒ $\left|x_2\right|$  ≥  a và $\left|x_1\right|$ ≥  a

                                                        ⇒ $\left|x_2\right|$+$\left|x_1\right|$ ≥  a + a = 2a  (2)

Từ (1) và (2) ta có: x₂ – x₁ ≥  2a ⇒ (x₂ – x₁)² ≥  (2a)²  

Ta lại có: (y₂ – y₁)²  ≥ 0

⇒  (x₂ – x₁)² + (y₂ – y₁)²  ≥  (2a)²  + 0 = (2a)²  

⇒ $\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$ ≥  2a  hay M₁M₂ ≥ A₁A₂

Vậy M₁M₂ nhỏ nhất khi M₁M₂ = A₁A₂

Dấu “=” xảy ra khi diểm M₁ ≡ A₁(-a; 0) và  M₂  ≡ A₂(a; 0).

Bài 7.37 trang 59 Toán 10 Tập 2:

Một cột trụ hình hyperbol (H.7.36), có chiều cao 6m, chỗ nhỏ nhất ở chính giữa và rộng 0,8m, đỉnh cột và đáy cột đều rộng 1m. Tính độ rộng của cột ở độ cao 5m (Tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).

Lời giải 

Chọn hệ trục tọa độ Oxy có gốc O là chỗ nhỏ nhất ở chính giữa, như hình vẽ sau:

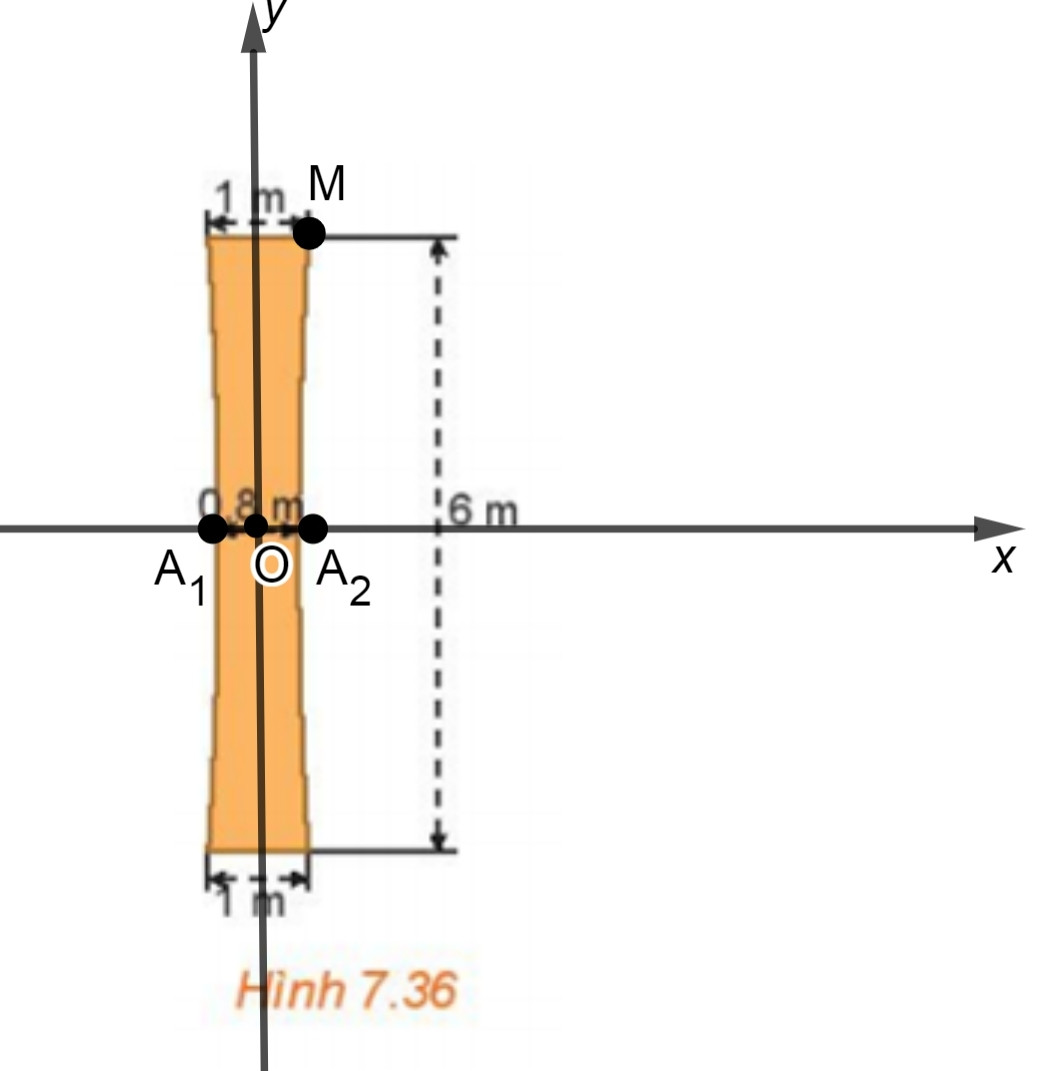
Gọi A₁, A₂ lần lượt là giao điểm của hypebol với trục hoành mà O là trung điểm của A₁A₂ nên A₁(−0,4 ; 0),  A₂(0,4 ; 0) hay a = 0,4.

Gọi phương trình hypebol của hình trụ có dạng : $\frac{x^2}{{\mathrm{0,4}}^2}-\frac{y^2}{b^2}=1$.

Gọi M là một điểm trên đỉnh cột nằm ở nhánh bên phải của trục tung hypebol. Ta có toạ độ điểm M(0,5; 3).

Vì điểm M(0,5; 3) thuộc (H) nên $\frac{{\mathrm{0,5}}^2}{{\mathrm{0,4}}^2}-\frac{3^2}{b^2}=1$

⇔$\frac{25}{16}-\frac{3^2}{b^2}=1$

⇔$\frac{3^2}{b^2}=\frac{25}{16}-1=\frac{9}{16}$ 

⇒ b² = 16

Do đó phương trình hypebol của hình trụ đó là: $\frac{x^2}{{\mathrm{0,4}}^2}-\frac{y^2}{16}=1$

Tại vị trí 5m thì điểm đó cách trục hoành một khoảng bằng 2m nên ta có y = 2.

Thay y = 2 vào phương trình hypebol ta được:

$\frac{x^2}{{\mathrm{0,4}}^2}-\frac{2^2}{16}=1$

⇔$\frac{x^2}{{\mathrm{0,4}}^2}=\frac{20}{16}$

⇒ x² = 0,2 ⇒x =$\sqrt{\mathrm{0,2}}$≈±0,45

Vậy độ rộng tại vị trí có độ cao 5m xấp xỉ là: 0,45.2 = 0,9 m.