Toán 10 Kết nối tri thức 10 Bài 11: Tích vô hướng của hai vecto

Giải Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vecto

Hamchoi.vn trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vecto sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 11. Mời các bạn đón xem:

1389 lượt xem

« Trang trước

Trang sau »

Giải bài tập Toán 10 Bài 11: Tích vô hướng của hai vecto

1. Góc giữa hai vecto

HĐ 1 trang 66 Toán 10 Tập 1: Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ $\vec{A B}$ và $\vec{A C}$ . Hãy tìm số đo các góc giữa $\vec{B C}$ và $\vec{B D}$ , $\vec{D A}$ và $\vec{D B}$ .

Lời giải

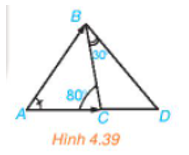
Số đo góc giữa hai vectơ $\vec{B C}$ và $\vec{B D}$ là góc CBD bằng 30°.

Xét tam giác BCD có $\hat{B C A}$ là góc ngoài của tam giác tại đỉnh C nên:

$\hat{B C A} = \hat{C B D} + \hat{C D B} \Rightarrow \hat{C D B} = \hat{B C A} - \hat{C B D} = 80 ° - 30 ° = 50 °$

$\Rightarrow \hat{A D B} = 50 °$

Suy ra số đo góc giữa hai vectơ $\vec{D A}$ và $\vec{D B}$ là góc ADB bằng 50°.

Vậy số đo góc giữa hai vectơ $\vec{B C}$ và $\vec{B D}$ bằng 30° và số đo góc giữa hai vectơ $\vec{D A}$ và $\vec{D B}$ bằng 50°.

Câu hỏi trang 66 Toán 10 Tập 1: Khi nào thì góc giữa hai vectơ bằng 0^°, bằng 180^°.

Lời giải

Góc giữa hai vectơ bằng 0° khi hai vectơ cùng hướng.

Góc giữa hai vectơ bằng 180° khi hai vectơ ngược hướng.

Luyện tập 1 trang 66 Toán 10 Tập 1: Cho tam giác đều ABC. Tính $(\vec{A B}, \vec{B C}) .$

Lời giải

Cho tam giác đều ABC. Tính ( vecto AB, vecto BC) (ảnh 1)

Câu hỏi trang 67 Toán 10 Tập 1: Khi nào tích vô hướng của hai vectơ khác vectơ-không $\vec{u}, \vec{v}$ là một số dương? Là một số âm?

Lời giải

Tích vô hướng của hai vectơ $\vec{u}, \vec{v} \neq \vec{0}$ được tính bởi công thức sau:

$\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}| . c os (\vec{u}, \vec{v}) .$

Vì $|\vec{u}| > 0, |\vec{v}| > 0$ nên dấu của tích vô hướng $\vec{u} . \vec{v}$ phụ thuộc vào dấu của $c os (\vec{u}, \vec{v})$ .

+) Tích vô hướng của hai vectơ $\vec{u} . \vec{v}$ là một số dương thì $c os (\vec{u}, \vec{v}) > 0$

Khi đó góc giữa hai vectơ $\vec{u}, \vec{v}$ là góc nhọn hoặc bằng 0°.

+) Tích vô hướng của hai vectơ $\vec{u}, \vec{v}$ là một số âm thì $c os (\vec{u}, \vec{v}) < 0.$

Khi đó góc giữa hai vectơ $\vec{u}, \vec{v}$ là góc tù hoặc bằng 180°.

Vậy khi $0 ° \leq (\vec{u}, \vec{v}) < 90 °$ thì tích vô hướng của hai vectơ $\vec{u}, \vec{v}$ là một số dương;

Khi $90 ° < (\vec{u}, \vec{v}) \leq 180 °$ thì tích vô hướng của hai vectơ $\vec{u}, \vec{v}$ là một số âm.

Câu hỏi trang 67 Toán 10 Tập 1: Khi nào thì ${(\vec{u} . \vec{v})}^{2} = {\vec{u}}^{2} . {\vec{v}}^{2} ?$

Lời giải

Khi nào thì (vecto u. vecto v)^2 = vecto u ^2. vecto v^2 (ảnh 1)

2. Tích vô hướng của hai vecto

Luyện tập 2 trang 67 Toán 10 Tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính $\vec{A B} . \vec{A C}$ theo a, b, c.

Lời giải

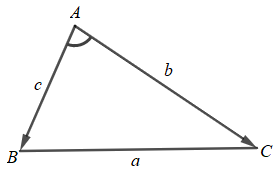
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính vecto AB.AC theo a,b,c (ảnh 1)

Ta có: $\vec{A B} . \vec{A C} = A B . A C . c os (\vec{A B}, \vec{A C})$

$\Rightarrow \vec{A B} . \vec{A C} = A B . A C . \cos \hat{B A C}$

$\Rightarrow \vec{A B} . \vec{A C} = b c . c os \hat{B A C}$

Xét tam giác ABC, theo định lí côsin ta có: $c o s \hat{B A C} = \frac{A C^{2} + A B^{2} - B C^{2}}{2 A C . A B}$

$\Rightarrow cos \hat{BAC} = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

$\Rightarrow \vec{A B} . \vec{A C} = b c . \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{b^{2} + c^{2} - a^{2}}{2}$

Vậy $\vec{A B} . \vec{A C} = \frac{b^{2} + c^{2} - a^{2}}{2} .$

3. Biểu thức tọa độ và tính chất của tích vô hướng

HĐ 2 trang 68 Toán 10 Tập 1: Cho hai vectơ cùng phương $\vec{u} = (x; y)$ và $\vec{v} = (k x; k y) .$ Hãy kiểm tra công thức $\vec{u} . \vec{v} = k (x^{2} + y^{2})$ theo từng trường hợp sau:

a) $\vec{u} = \vec{0};$

b) $\vec{u} \neq \vec{0}$ và $k \geq 0;$

c) $\vec{u} \neq \vec{0}$ và k < 0.

Lời giải

Ta có: $\vec{u} = (x; y)$ $\Rightarrow |\vec{u}| = \sqrt{x^{2} + y^{2}}$

$\vec{v} = (k x; k y) \Rightarrow |\vec{v}| = \sqrt{{(k x)}^{2} + {(k y)}^{2}} = \sqrt{k^{2} x^{2} + k^{2} y^{2}} = \sqrt{k^{2} (x^{2} + y^{2})} = |k| \sqrt{x^{2} + y^{2}}$

a) Vì vectơ $\vec{0}$ vuông góc với mọi vectơ nên vectơ $\vec{v}$ vuông góc với $\vec{u} = \vec{0}$

Do đó $\vec{u} ⊥ \vec{v} \Leftrightarrow \vec{u} . \vec{v} = 0$

Ta có: $\vec{u} = \vec{0} \Rightarrow \vec{u} = (0; 0) \Rightarrow \{\begin{cases} x = 0 \\ y = 0 \end{cases}$

Do đó $k (x^{2} + y^{2}) = k (0^{2} + 0^{2}) = 0$

$\Rightarrow \vec{u} . \vec{v} = k (x^{2} + y^{2}) = 0$

Vậy với $\vec{u} = \vec{0}$ thì công thức $\vec{u} . \vec{v} = k (x^{2} + y^{2})$ đúng.

b) Vì k ≥ 0 nên vectơ $\vec{v} = (k x; k y)$ cùng hướng với vectơ $\vec{u} = (x; y)$

$\Rightarrow (\vec{u}, \vec{v}) = 0 °$

Do đó $\vec{u} . \vec{v} = |\vec{u}| |\vec{v}| c o s (\vec{u}, \vec{v})$

$= \sqrt{x^{2} + y^{2}} . |k| \sqrt{x^{2} + y^{2}} . c os 0 ° = k . (x^{2} + y^{2}) .1 = k (x^{2} + y^{2})$

Vậy với $\vec{u} \neq \vec{0}$ và $k \geq 0$ thì công thức $\vec{u} . \vec{v} = k (x^{2} + y^{2})$ đúng.

c) Vì k < 0 nên vectơ $\vec{v} = (k x; k y)$ ngược hướng với vectơ $\vec{u} = (x; y)$

$\Rightarrow (\vec{u}, \vec{v}) = 180 °$

Do đó: $\vec{u} . \vec{v} = |\vec{u}| |\vec{v}| c o s (\vec{u}, \vec{v})$

$= \sqrt{x^{2} + y^{2}} . |k| \sqrt{x^{2} + y^{2}} . c os18 0 ° = - k . (x^{2} + y^{2}) . (- 1) = k (x^{2} + y^{2})$

Vậy với $\vec{u} \neq \vec{0}$ và k < 0 thì công thức $\vec{u} . \vec{v} = k (x^{2} + y^{2})$ đúng.

HĐ 3 trang 68 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương $\vec{u} = (x; y)$ và $\vec{v} = (x'; y')$ .

a) Xác định tọa độ các điểm A và B sao cho $\vec{O A} = \vec{u}, \vec{O B} = \vec{v} .$

b) Tính AB², OA², OB² theo tọa độ của A và B.

c) Tính $\vec{O A} . \vec{O B}$ theo tọa độ của A, B.

Lời giải

a) Vì $\vec{O A} = \vec{u}$ mà $\vec{u} = (x; y)$ nên $\vec{O A} = (x; y)$ suy ra A(x; y).

Vì $\vec{O B} = \vec{v}$ mà $\vec{v} = (x'; y')$ nên $\vec{O B} = (x^{'}; y^{'})$ suy ra B(x'; y').

b) +) Ta có: A(x; y) và B(x'; y') $\Rightarrow \vec{A B} = (x' - x; y' - y)$

$\Rightarrow A B = \sqrt{{(x' - x)}^{2} + {(y' - y)}^{2}}$

$\Rightarrow A B^{2} = {(x' - x)}^{2} + {(y' - y)}^{2} .$

+) Ta có :

$\vec{O A} = (x; y) \Rightarrow O A = \sqrt{x^{2} + y^{2}} \Rightarrow O A^{2} = x^{2} + y^{2} .$

+) Ta có:

$\vec{O B} = (x'; y') \Rightarrow O B = \sqrt{x'^{2} + y'^{2}} \Rightarrow O B^{2} = x'^{2} + y'^{2} .$

Vậy $A B^{2} = {(x' - x)}^{2} + {(y' - y)}^{2};$ $O A^{2} = x^{2} + y^{2}$ và $O B^{2} = x'^{2} + y'^{2} .$

c) Ta có: $\vec{O A} . \vec{O B} = O A . O B . c o s (\vec{O A}, \vec{O B}) = O A . O B . c o s \hat{A O B}$

Xét tam giác OAB, theo định lí côsin ta có:

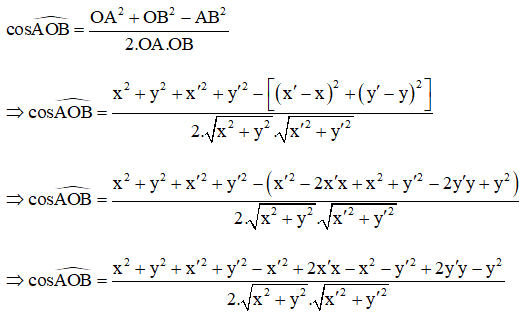
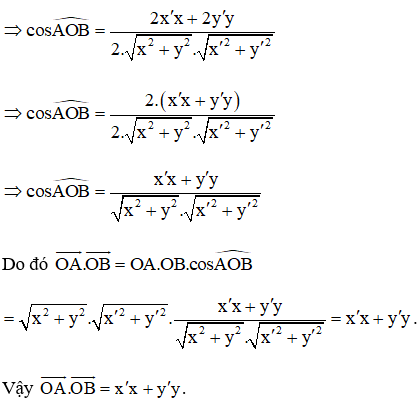
Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương (ảnh 1)

Luyện tập 3 trang 68 Toán 10 Tập 1: Tính tích vô hướng và góc giữa hai vectơ $\vec{u} = (0; - 5), \vec{v} = (\sqrt{3}; 1)$

Lời giải

Giải Toán 10 Bài 11: Tích vô hướng của hai vecto - Kết nối tri thức (ảnh 1)

Vậy $\vec{u} . \vec{v} = - 5$ và góc giữa hai vectơ $\vec{u}, \vec{v}$ bằng 120°.

HĐ 4 trang 68 Toán 10 Tập 1: Cho ba vectơ $\vec{u} = (x_{1}; y_{1}),$ $\vec{v} = (x_{2}; y_{2}),$ $\vec{w} = (x_{3}; y_{3}) .$

a) Tính $\vec{u} . (\vec{v} + \vec{w}), \vec{u} . \vec{v} + \vec{u} . \vec{w}$ theo tọa độ các vectơ $\vec{u}, \vec{v}, \vec{w} .$

b) So sánh $\vec{u} . (\vec{v} + \vec{w})$ và $\vec{u} . \vec{v} + \vec{u} . \vec{w}$ .

c) So sánh $\vec{u} . \vec{v}$ và $\vec{v} . \vec{u}$ .

Lời giải

a) Với $\vec{u} = (x_{1}; y_{1}), \vec{v} = (x_{2}; y_{2})$ và $\vec{w} = (x_{3}; y_{3})$ ta có:

+) $\vec{v} + \vec{w} = (x_{2} + x_{3}; y_{2} + y_{3})$

$\Rightarrow \vec{u} . (\vec{v} + \vec{w})$ $= x_{1} . (x_{2} + x_{3}) + y_{1} . (y_{2} + y_{3}) = x_{1} . x_{2} + x_{1} . x_{3} + y_{1} . y_{2} + y_{1} . y_{3}$ .

+) $\vec{u} . \vec{v} = x_{1} . x_{2} + y_{1} . y_{2}$ và $\vec{u} . \vec{w} = x_{1} . x_{3} + y_{1} . y_{3}$

$\Rightarrow \vec{u} . \vec{v} + \vec{u} . \vec{w} = x_{1} . x_{2} + y_{1} . y_{2} + x_{1} . x_{3} + y_{1} . y_{3}$ .

b) Theo câu a ta có:

$\vec{u} . (\vec{v} + \vec{w}) = x_{1} . x_{2} + y_{1} . y_{2} + x_{1} . x_{3} + y_{1} . y_{3}$ và $\vec{u} . \vec{v} + \vec{u} . \vec{w} = x_{1} . x_{2} + y_{1} . y_{2} + x_{1} . x_{3} + y_{1} . y_{3}$

$\Rightarrow \vec{u} . (\vec{v} + \vec{w}) = \vec{u} . \vec{v} + \vec{u} . \vec{w} .$

Vậy $\vec{u} . (\vec{v} + \vec{w}) = \vec{u} . \vec{v} + \vec{u} . \vec{w} .$

c) Ta có: $\vec{u} . \vec{v} = x_{1} . x_{2} + y_{1} . y_{2}$ và $\vec{v} . \vec{u} = x_{2} . x_{1} + y_{2} . y_{1} = x_{1} . x_{2} + y_{1} . y_{2} .$

$\Rightarrow \vec{u} . \vec{v} = \vec{v} . \vec{u} .$

Vậy $\vec{u} . \vec{v} = \vec{v} . \vec{u} .$

Luyện tập 4 trang 70 Toán 10 Tập 1: Cho tam giác ABC với A(‒1;2), B(8;‒1), C(8;8). Gọi H là trực tâm của tam giác.

a) Chứng minh rằng $\vec{A H} . \vec{B C} = 0$ và $\vec{B H} . \vec{C A} = 0$

b) Tìm tọa độ của H.

c) Giải tam giác ABC.

Lời giải

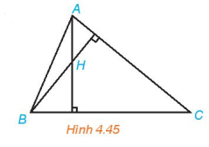
a) Vì H là trực tâm của tam giác ABC nên:

+) $A H ⊥ B C \Rightarrow \vec{A H} ⊥ \vec{B C} \Rightarrow \vec{A H} . \vec{B C} = 0;$

+) $B H ⊥ C A \Rightarrow \vec{B H} ⊥ \vec{C A} \Rightarrow \vec{B H} . \vec{C A} = 0$ .

Vậy $\vec{A H} . \vec{B C} = 0$ và $\vec{B H} . \vec{C A} = 0$ .

b) Gọi tọa độ điểm H là H(x; y).

Ta có: A(‒1;2), B(8;‒1), C(8;8) và H(x; y).

$\Rightarrow \vec{A H} = (x + 1; y - 2); \vec{B C} = (0; 9)$ và $\vec{B H} = (x - 8; y + 1); \vec{A C} = (9; 6)$

Suy ra $\vec{A H} . \vec{B C} = (x + 1) .0 + (y - 2) .9 = 9 (y - 2) .$

Và $\vec{B H} . \vec{A C} = (x - 8) .9 + (y + 1) .6 = 9 x - 72 + 6 y + 6 = 9 x + 6 y - 66$ .

Theo câu a ta có: $\vec{A H} . \vec{B C} = 0$ $\Leftrightarrow$ 9(y – 2) = 0 $\Leftrightarrow$ y – 2 = 0 $\Leftrightarrow$ y = 2.

Và $\vec{B H} . \vec{A C} = 0$ (do BH ⊥ AC) $\Leftrightarrow$ 9x + 6y – 66 = 0.

Thay y = 2 vào 9x + 6y – 66 = 0 ta được: 9x + 6.2 – 66 = 0

$\Leftrightarrow$ 9x – 54 = 0

$\Leftrightarrow$ 9x = 54

$\Leftrightarrow$ x = 6

⇒ H(6; 2)

Vậy H(6; 2).

c) Với A(‒1;2), B(8;‒1), C(8;8) ta có:

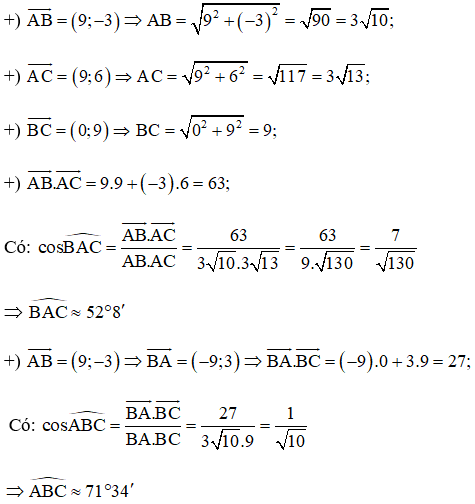
Cho tam giác ABC với A(‒1;2), B(8;‒1), C(8;8). Gọi H là trực tâm (ảnh 1)

Xét tam giác ABC, theo định lí tổng ba góc trong một tam giác ta có: $\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$

$\Rightarrow \hat{A C B} = 180 ° - (\hat{B A C} + \hat{A B C})$

$\Rightarrow \hat{A C B} \approx 180 ° - (52 ° 8^{'} + 71 ° 34^{'}) \approx 56 ° 18^{'}$

Vậy

$A B = 3 \sqrt{10}, A C = 3 \sqrt{13}, B C = 9, \hat{B A C} \approx 52 ° 8^{'}, \hat{A B C} \approx 71 ° 34^{'}, \hat{A C B} \approx 56 ° 18^{'} .$

Vận dụng trang 70 Toán 10 Tập 1: Một lực $\vec{F}$ không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực $\vec{F}$ được phân tích thành hai lực thành phần $\vec{F_{1}}$ và $\vec{F_{2}}$ $(\vec{F} = \vec{F_{1}} + \vec{F_{2}})$

a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực $\vec{F}$ (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực $\vec{F_{1}}$ và $\vec{F_{2}}$

b) Giả sử các lực thành phần $\vec{F_{1}}$ và $\vec{F_{2}}$ tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực $\vec{F}$ và lực $\vec{F_{1}}$

Lời giải

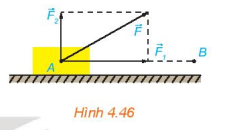
a) Một lực $\vec{F}$ tác động lên một vật làm vật dịch chuyển tịnh tiến theo một vectơ độ rời $\vec{s} .$

+) Công sinh bởi lực $\vec{F}$ là $A_{\vec{F}} = \vec{F} . \vec{s}$

+) Công sinh bởi lực $\vec{F_{1}}$ là $A_{\vec{F_{1}}} = \vec{F_{1}} . \vec{s}$

+) Công sinh bởi lực $\vec{F_{2}}$ là $A_{\vec{F_{2}}} = \vec{F_{2}} . \vec{s}$

Suy ra $A_{\vec{F_{1}}} + A_{\vec{F_{2}}} = \vec{F_{1}} . \vec{s} + \vec{F_{2}} . \vec{s} = (\vec{F_{1}} + \vec{F_{2}}) . \vec{s}$ (tính chất phân phối đối với phép cộng của tích vô hướng)

Mà $\vec{F} = \vec{F_{1}} + \vec{F_{2}}$ do đó $A_{\vec{F_{1}}} + A_{\vec{F_{2}}} = (\vec{F_{1}} + \vec{F_{2}}) . \vec{s} = \vec{F} . \vec{s} = A_{\vec{F}}$

Vậy $A_{\vec{F}} = A_{\vec{F_{1}}} + A_{\vec{F_{2}}} .$

b) +) Công sinh bởi lực $\vec{F}$ là $A_{\vec{F}} = \vec{F} . \vec{s} = F . s . c os (\vec{F}, \vec{s})$

Do vật chuyển động thẳng từ A đến B nên $\vec{s}$ cùng hướng với $\vec{F_{1}}$ .

Suy ra $(\vec{F}, \vec{s}) = (\vec{F}, \vec{F_{1}})$

Do đó $A_{\vec{F}} = F . s . c os (\vec{F}, \vec{F_{1}})$

Ta lại có: $F_{1} = F . c os (\vec{F}, \vec{F_{1}})$

$\Rightarrow A_{\vec{F}} = F_{1} . s$ (1)

+) Công sinh bởi lực $\vec{F_{1}}$ là $A_{\vec{F_{1}}} = \vec{F_{1}} . \vec{s} = F_{1} . s . c os (\vec{F_{1}}, \vec{s})$

Do $\vec{s}$ cùng hướng với $\vec{F_{1}}$ nên $(\vec{F_{1}}, \vec{s}) = 0 °$

$\Rightarrow A_{\vec{F_{1}}} = F_{1} . s . c {os0}^{0} = F_{1} . s$ (2)

Từ (1) và (2) suy ra $A_{\vec{F}} = A_{\vec{F_{1}}} (= F_{1} . s)$ .

Vậy $A_{\vec{F}} = A_{\vec{F_{1}}} .$

Bài tập

Bài 4.21 trang 70 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ trong mỗi trường hợp sau:

a) $\vec{a} = (- 3; 1), \vec{b} = (2; 6);$

b) $\vec{a} = (3; 1), \vec{b} = (2; 4);$

c) $\vec{a} = (- \sqrt{2}; 1), \vec{b} = (2; - \sqrt{2});$

Lời giải

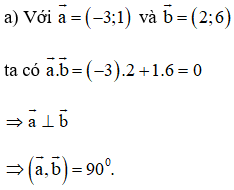
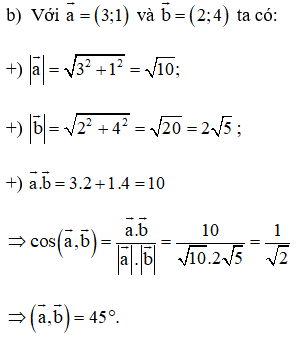
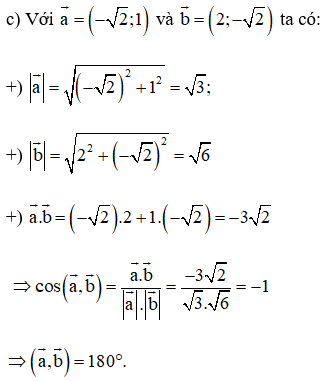
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ a và vecto b (ảnh 1)

Bài 4.22 trang 70 Toán 10 Tập 1: Tìm điều kiện của $\vec{u}, \vec{v}$ để:

a) $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}|;$

b) $\vec{u} . \vec{v} = - |\vec{u}| . |\vec{v}|;$

Lời giải

a) Ta có: $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v})$

Để $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}|$ thì $|\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v}) = |\vec{u}| . |\vec{v}|$

$\Leftrightarrow \cos (\vec{u}, \vec{v}) = 1 \Leftrightarrow (\vec{u}, \vec{v}) = 0 °$

Suy ra $\vec{u}, \vec{v}$ là hai vectơ cùng hướng.

Vậy hai vectơ $\vec{u}, \vec{v}$ cùng hướng thì $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}| .$

b) Ta có: $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v})$

Để $\vec{u} . \vec{v} = - |\vec{u}| . |\vec{v}|$ thì $|\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v}) = - |\vec{u}| . |\vec{v}|$

$\Leftrightarrow \cos (\vec{u}, \vec{v}) = - 1 \Leftrightarrow (\vec{u}, \vec{v}) = 180 °$

Suy ra $\vec{u}, \vec{v}$ là hai vectơ ngược hướng.

Vậy hai vectơ $\vec{u}, \vec{v}$ ngược hướng thì $\vec{u} . \vec{v} = - |\vec{u}| . |\vec{v}| .$

Bài 4.23 trang 70 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 2), B(‒4; 3). Gọi M(t; 0) là một điểm thuộc trục hoành.

a) Tính $\vec{A M} . \vec{B M}$ theo t;

b) Tính t để $\hat{A M B} = 90 ° .$

Lời giải

a) Với A(1; 2), B(‒4; 3) và M(t; 0) ta có:

$\vec{A M} = (t - 1; - 2), \vec{B M} = (t + 4; - 3)$

$\Rightarrow \vec{A M} . \vec{B M} = (t - 1) (t + 4) + (- 2) . (- 3) = t^{2} + 3 t - 4 + 6 = t^{2} + 3 t + 2.$

b) Để $\hat{A M B} = 90 °$ thì $\vec{M A} . \vec{M B} = 0 \Leftrightarrow \vec{A M} . \vec{B M} = 0$

$\Leftrightarrow t^{2} + 3 t + 2 = 0 \Leftrightarrow (t + 1) (t + 2) = 0 \Leftrightarrow [\begin{array}{l} t = - 1 \\ t = - 2 \end{array}$

Vậy với $t \in \{- 1; - 2\}$ thì $\hat{A M B} = 90 ° .$

Bài 4.24 trang 70 SGK Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4), C(2; ‒2).

a) Giải tam giác ABC.

b) Tìm tọa độ trực tâm H của tam giác ABC.

Lời giải

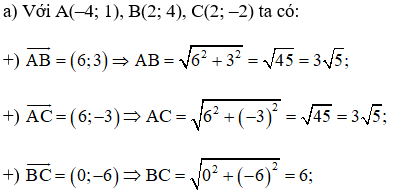
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4) (ảnh 1)

+) Theo định lí cosin, ta có:

$cos A = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{{(3 \sqrt{5})}^{2} + {(3 \sqrt{5})}^{2} - 6^{2}}{2.3 \sqrt{5} .3 \sqrt{5}} = \frac{54}{90} = \frac{3}{5}$

$\Rightarrow \hat{A} \approx 53 ° 8'$

Tam giác ABC có AB = AC nên tam giác ABC cân tại A

$\Rightarrow \hat{B} = \hat{C} = \frac{180^{0} - \hat{A}}{2} \approx \frac{180 ° - 53 ° 8'}{2} = 63 ° 26'$ .

Vậy: $A B = A C = 3 \sqrt{5}, B C = 6, \hat{A} \approx 53 ° 8', \hat{B} = \hat{C} \approx 63 ° 26' .$

b) Giả sử trực tâm H của tam giác ABC có tọa độ là H(x; y).

Do H là trực tâm của tam giác ABC nên $A H ⊥ B C; B H ⊥ A C$ $\Leftrightarrow \vec{A H} ⊥ \vec{B C}; \vec{B H} ⊥ \vec{A C}$

Với A(‒4; 1), B(2; 4), C(2; ‒2) và H(x; y) ta có:

$\vec{A H} = (x + 4; y - 1); \vec{B C} = (0; - 6); \vec{B H} = (x - 2; y - 4); \vec{A C} = (6; - 3)$

Vì $\vec{A H} ⊥ \vec{B C}$ nên $\vec{A H} . \vec{B C} = 0$ $\Leftrightarrow$ (x + 4).0 + (y – 1).(‒6) = 0 $\Leftrightarrow$ ‒6.(y – 1) = 0 $\Leftrightarrow$ y = 1.

Vì $\vec{B H} ⊥ \vec{A C}$ nên $\vec{B H} . \vec{A C} = 0$ Û (x – 2).6 + (y – 4).(‒3) = 0

(x – 2).2 + (y – 4).(‒1) = 0 Û 2x – y = 0.

Mà y = 1 $\Rightarrow 2 x - 1 = 0 \Leftrightarrow x = \frac{1}{2} .$

Vậy toạ độ trực tâm H của tam giác ABC là $H (\frac{1}{2}; 1)$ .

Bài 4.25 trang 70 Toán 10 Tập 1: Chứng minh rằng với mọi tam giác ABC:

$S_{A B C} = \frac{1}{2} \sqrt{{\vec{A B}}^{2} . {\vec{A C}}^{2} - {(\vec{A B} . \vec{A C})}^{2}} .$

Lời giải

Cách 1:

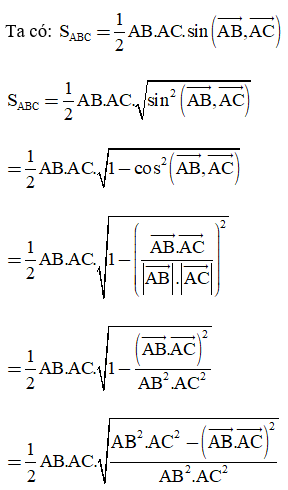
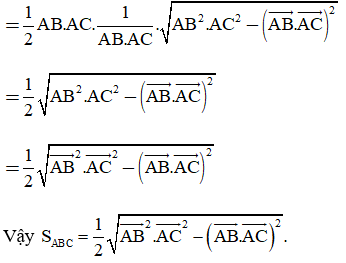
Chứng minh rằng với mọi tam giác ABC, ta có (ảnh 1)

Cách 2:

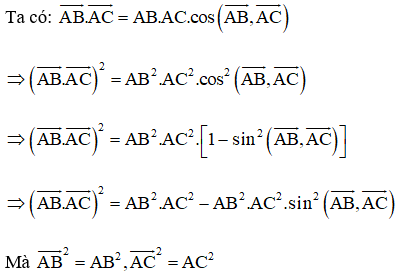
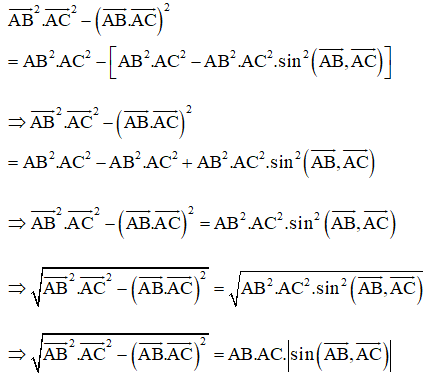
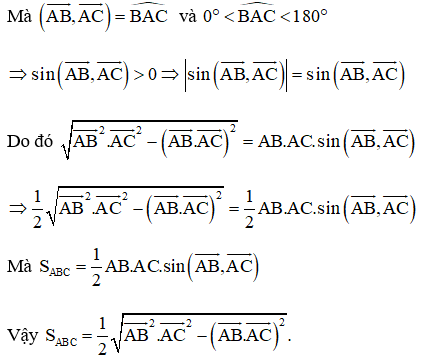
Chứng minh rằng với mọi tam giác ABC, ta có (ảnh 1)

Bài 4.26 trang 70 Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M,

MA² + MB² + MC² = 3MG² + GA² + GB² + GC².

Lời giải

$M A^{2} + M B^{2} + M C^{2} = {\vec{M A}}^{2} + {\vec{M B}}^{2} + {\vec{M C}}^{2}$

$= {(\vec{M G} + \vec{G A})}^{2} + {(\vec{M G} + \vec{G B})}^{2} + {(\vec{M G} + \vec{G C})}^{2}$ (Quy tắc ba điểm)

$= {\vec{M G}}^{2} + 2 \vec{M G} . \vec{G A} + {\vec{G A}}^{2} + {\vec{M G}}^{2} + 2 \vec{M G} . \vec{G B} + {\vec{G B}}^{2} + {\vec{M G}}^{2} + 2 \vec{M G} . \vec{G C} + {\vec{G C}}^{2} = ({\vec{M G}}^{2} + {\vec{M G}}^{2} + {\vec{M G}}^{2}) + (2 \vec{M G} . \vec{G A} + 2 \vec{M G} . \vec{G B} + 2 \vec{M G} . \vec{G C}) + {\vec{G A}}^{2} + {\vec{G B}}^{2} + {\vec{G C}}^{2}$

$= 3 {\vec{M G}}^{2} + 2 \vec{M G} . (\vec{G A} + \vec{G B} + \vec{G C}) + {\vec{G A}}^{2} + {\vec{G B}}^{2} + {\vec{G C}}^{2}$

Vì G là trọng tâm tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ (tính chất trọng tâm tam giác)

$\Rightarrow \vec{M G} . (\vec{G A} + \vec{G B} + \vec{G C}) = \vec{M G} . \vec{0} = 0$

$\Rightarrow M A^{2} + M B^{2} + M C^{2} = 3 {\vec{M G}}^{2} + {\vec{G A}}^{2} + {\vec{G B}}^{2} + {\vec{G C}}^{2} .$

$\Rightarrow$ MA² + MB² + MC² = 3MG² + GA² + GB² + GC².

Vậy MA² + MB² + MC² = 3MG² + GA² + GB² + GC².

Bài viết liên quan

1389 lượt xem

« Trang trước

Trang sau »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vecto

Bài viết liên quan

Có thể bạn quan tâm