Cho hình chữ nhật ABCD có AB = 4 cm, BC = 3 cm. Kẻ BH vuông góc với AC tại H, tia BH cắt AD ở E.
1) Tính AC, BH, \(\widehat {BAC}\).
2) Chứng minh BH.BE = CD2.
3) Kẻ EF vuông góc với BC tại F. Chứng minh .
4) Tính diện tích tam giác BHF.
Giải bởi Vietjack
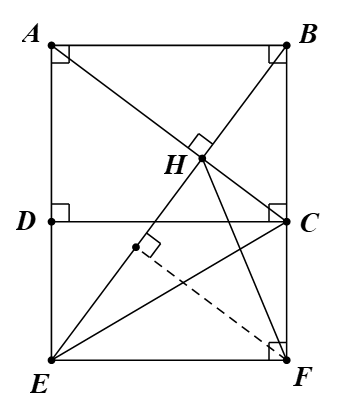
1) Tam giác ABC vuông tại B (do ABCD là hình chữ nhật) có BH là đường cao:
⦁ AC2 = AB2 + BC2 (Định lí Pythagore).
= 42 + 32 = 25.
Suy ra AC = 5 (cm).
⦁ \(\frac{1}{{B{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\) (Hệ thức lượng trong tam giác vuông).
\( = \frac{1}{{{4^2}}} + \frac{1}{{{3^2}}} = \frac{{25}}{{144}}\).
Suy ra \(B{H^2} = \frac{{144}}{{25}}\).
Khi đó \(BH = \frac{{12}}{5}\) (cm).
⦁ \(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{3}{4}\). Suy ra \(\widehat {BAC} \approx 36^\circ 52'\).
Vậy AC = 5 cm; \(BH = \frac{{12}}{5}\) cm và \(\widehat {BAC} \approx 36^\circ 52'\).
2) Ta có AB = CD (do ABCD là hình chữ nhật).
Tam giác ABE vuông tại A có AH là đường cao:
AB2 = BH.BE (Hệ thức lượng trong tam giác vuông).
Vậy BH.BE = CD2 (điều phải chứng minh).
3) Xét ∆BHC và ∆BFE, có:
\(\widehat {HBC}\) chung;
\(\widehat {BHC} = \widehat {BFE} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{BH}}{{BF}} = \frac{{BC}}{{BE}}\).
Xét ∆BHF và ∆BCE, có:
\(\widehat {HBC}\) chung;
\(\frac{{BH}}{{BC}} = \frac{{BF}}{{BE}}\) (do \(\frac{{BH}}{{BF}} = \frac{{BC}}{{BE}}\)).
Vậy (c.g.c).
4) Ta có CDEF là hình chữ nhật (do \(\widehat {CDE} = \widehat {DCF} = \widehat {CFE} = 90^\circ \)).
Suy ra EF = CD = AB = 4 (cm).
Vì \(\frac{{BH}}{{BF}} = \frac{{BC}}{{BE}}\) nên BC.BF = BH.BE = CD2 = AB2 = 16 (cm).
Suy ra \(BF = \frac{{16}}{{BC}} = \frac{{16}}{3}\) (cm).
Khi đó \({S_{\Delta BFE}} = \frac{1}{2}BF.EF = \frac{1}{2}.\frac{{16}}{3}.4 = \frac{{32}}{3}\) (cm2).
Tam giác BFE vuông tại F: BE2 = BF2 + EF2 (Định lí Pythagore).
Suy ra \[BE = \sqrt {B{F^2} + E{F^2}} = \sqrt {{{\left( {\frac{{16}}{3}} \right)}^2} + {4^2}} = \frac{{20}}{3}\] (cm).
Ta thấy tam giác BEF và tam giác BHF có chung đường cao hạ từ điểm F.
Suy ra \(\frac{{{S_{\Delta BHF}}}}{{{S_{\Delta BEF}}}} = \frac{{BH}}{{BE}} = \frac{{12}}{5}:\frac{{20}}{3} = \frac{9}{{25}}\).
Vậy \({S_{\Delta BHF}} = \frac{9}{{25}}.{S_{\Delta BEF}} = \frac{9}{{25}}.\frac{{32}}{3} = \frac{{96}}{{25}}\) (cm2).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Với a, b, c là các số thực không âm thỏa mãn a + b + c = 2. Tìm giá trị lớn nhất của P = a + 2b2 + 3c3.
Cho tam giác ABC đều cạnh bằng a, M là điểm di động trên đường thẳng AC. Tìm giá trị nhỏ nhất của biểu thức \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} } \right|\).
Tìm tất cả các nghiệm nguyên dương của phương trình 6x2 + 5y2 = 74.
Hỏi phương trình 3x2 – 6x + ln(x + 1)3 + 1 = 0 có bao nhiêu nghiệm phân biệt?
Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz. Tìm giá trị lớn nhất của biểu thức \(P = \frac{1}{{\sqrt {1 + {x^2}} }} + \frac{1}{{\sqrt {1 + {y^2}} }} + \frac{1}{{\sqrt {1 + {z^2}} }}\).
Tìm các số nguyên x để giá trị của đa thức a(x) = x3 – 2x2 + 3x + 50 chia hết cho giá trị của đa thức b(x) = x + 3.
Tìm số tự nhiên x có 3 chữ số, biết rằng nếu viết thêm chữ số 9 vào bên trái số đó ta được một số gấp 26 lần số ban đầu.
Vẽ \[\widehat {xOy} = 50^\circ \]. Lấy điểm M thuộc Ox sao cho OM = 6 cm. Vẽ đường thẳng d là trung trực của đoạn thẳng OM.
Tìm số tự nhiên x có 3 chữ số, biết rằng nếu viết thêm chữ số 9 vào bên trái số đó ta được số mới gấp 25 lần số cũ.
Khi đó, tìm số thập phân biểu diễn phân số \(\frac{x}{{100}}\).
Cho tam giác ABC vuông tại A, AB = 3 và AC = 4. Gọi I là tâm đường tròn nội tiếp của tam giác ABC. Chứng minh rằng \(5\overrightarrow {IA} + 4\overrightarrow {IB} + 3\overrightarrow {IC} = \vec 0\).
Với các số 0, 1, 3, 6, 9, có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau và không chia hết cho 3.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết rằng AB = a, \(AD = a\sqrt 3 \) và \(\widehat {ASB} = 60^\circ \). Tính diện tích khối cầu ngoại tiếp hình chóp S.ABCD.
Gọi m0 là giá trị thực của tham số m để parabol (P): y = x2 – 2x + 3 – m cắt trục hoành Ox tại hai điểm phân biệt A, B sao cho độ dài đoạn thẳng AB bằng 4. Tìm m0.
Tổng của ba số bằng 13,68. Biết rằng tổng của số thứ nhất và số thứ hai bằng 5,79; tổng của số thứ hai và số thứ ba bằng 12,45. Tìm ba số đó.
Cho hàm số \(y = f\left( x \right) = \frac{{12}}{x}\).
a) Tính f(5) và f(–3).
b) Hãy điền giá trị tương ứng của hàm số vào bảng sau:
|
x |
6 |
4 |
3 |
2 |
5 |
8 |
12 |
|
\(f\left( x \right) = \frac{{12}}{x}\) |
? |
? |
? |
? |
? |
? |
? |
