Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 72)
-
1252 lượt thi
-
46 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Tìm số tự nhiên x có 3 chữ số, biết rằng nếu viết thêm chữ số 9 vào bên trái số đó ta được một số gấp 26 lần số ban đầu.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \[\overline {abc} \] (a ≠ 0; a, b, c ∈ ℕ; 0 ≤ a, b, c ≤ 9).
Theo đề, ta có nếu viết thêm chữ số 9 vào bên trái số đó ta được một số gấp 26 lần số ban đầu.
Nghĩa là, \[\overline {9abc} = \overline {abc} \times 26\].
\( \Rightarrow 9 \times 1000 + \overline {abc} = \overline {abc} \times 26\).
\( \Rightarrow 9000 = \overline {abc} \times 25\).
\[ \Rightarrow \overline {abc} = 9000:25 = 360\].
Vậy số cần tìm là 360.
Câu 2:
Tìm số tự nhiên x có 3 chữ số, biết rằng nếu viết thêm chữ số 9 vào bên trái số đó ta được số mới gấp 25 lần số cũ.
Khi đó, tìm số thập phân biểu diễn phân số \(\frac{x}{{100}}\).
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \[\overline {abc} \] (a ≠ 0; a, b, c ∈ ℕ; 0 ≤ a, b, c ≤ 9).
Theo đề, ta có nếu viết thêm chữ số 9 vào bên trái số đó ta được số mới gấp 25 lần số cũ.
Nghĩa là, \[\overline {9abc} = \overline {abc} \times 25\].
\( \Rightarrow 9 \times 1000 + \overline {abc} = \overline {abc} \times 25\).
\( \Rightarrow 9000 = \overline {abc} \times 24\).
\[ \Rightarrow \overline {abc} = 9000:24 = 375\].
Vậy số cần tìm là 375.
Khi đó, số thập phân biểu diễn phân số \(\frac{x}{{100}}\) là: \(\frac{x}{{100}} = \frac{{375}}{{100}} = 3,75\).
Câu 3:
Cho x > y > 0 thỏa mãn 3x2 + 3y2 = 10xy. Tính giá trị của biểu thức \(P = \frac{{x - y}}{{x + y}}\).
 Xem đáp án
Xem đáp án
Ta có 3x2 + 3y2 = 10xy.
⇔ 3x2 – 10xy + 3y2 = 0.
⇔ 3x2 – 9xy – xy + 3y2 = 0.
⇔ 3x(x – 3y) – y(x – 3y) = 0.
⇔ (x – 3y)(3x – y) = 0.
⇔ x = 3y hoặc 3x = y.
So với điều kiện x > y > 0, ta nhận x = 3y.
Thế x = 3y vào P ta được: \(P = \frac{{x - y}}{{x + y}} = \frac{{3y - y}}{{3y + y}} = \frac{{2y}}{{4y}} = \frac{1}{2}\).
Vậy \(P = \frac{1}{2}\).
Câu 4:
Tìm a, b, c để đồ thị hàm số y = ax2 + bx + c là đường parabol có đỉnh I(3; 4), cắt trục hoành tại điểm có hoành độ bằng –1.
 Xem đáp án
Xem đáp án
Trục hoành: y = 0.
Suy ra giao điểm của parabol cần tìm và trục hoành là điểm A(–1; 0).
Ta có parabol đi qua điểm A(–1; 0).
Suy ra 0 = a – b + c (1)
Ta có parabol có đỉnh I(3; 4).
Suy ra \( - \frac{b}{{2a}} = 3\).
Do đó 6a + b = 0 (2)
Ta có parabol đi qua điểm I(3; 4).
Suy ra 4 = 9a + 3b + c (3)
Từ (1), (2), (3), ta có hệ phương trình: \(\left\{ \begin{array}{l}a - b + c = 0\\6a + b = 0\\9a + 3b + c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{4}\\b = \frac{3}{2}\\c = \frac{7}{4}\end{array} \right.\).
Vậy \(a = - \frac{1}{4};\,\,b = \frac{3}{2};\,\,c = \frac{7}{4}\).
Câu 5:
Tìm các số nguyên x để giá trị của đa thức a(x) = x3 – 2x2 + 3x + 50 chia hết cho giá trị của đa thức b(x) = x + 3.
 Xem đáp án
Xem đáp án
Ta có:
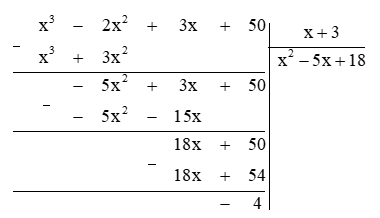
Khi đó \(\frac{{a\left( x \right)}}{{b\left( x \right)}} = \frac{{{x^3} - 2{x^2} + 3x + 50}}{{x + 3}} = {x^2} - 5x + 18 - \frac{4}{{x + 3}}\).
Để a(x) chia hết cho b(x) thì –4 phải chia hết cho (x + 3).
Tức là, x + 3 ∈ Ư(–4).
Ta có Ư(–4) = {–4; –2; –1; 1; 2; 4}.
Ta có bảng sau:
|
x + 3 |
–4 |
–2 |
–1 |
1 |
2 |
4 |
|
x |
–7 |
–5 |
–4 |
–2 |
–1 |
1 |
Vì x ∈ ℤ nên x ∈ {–7; –5; –4; –2; –1; 1}.
Vậy x ∈ {–7; –5; –4; –2; –1; 1} thỏa mãn yêu cầu bài toán.
Câu 6:
Cho đường thẳng d: y = –4x + 3.
a) Vẽ đồ thị hàm số.
b) Tìm tọa độ giao điểm A, B của d với lần lượt hai trục tọa độ Ox và Oy.
c) Tính khoảng cách từ gốc tọa độ đến d.
d) Tính diện tích tam giác OAB.
 Xem đáp án
Xem đáp án
a) Bảng giá trị:
|
x |
0 |
1 |
2 |
|
y |
3 |
–1 |
–5 |
Đồ thị:
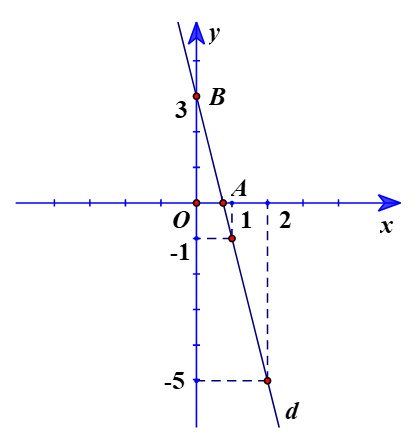
b) Trục Ox: y = 0.
Với y = 0, ta có: \[ - 4x + 3 = 0 \Leftrightarrow x = \frac{3}{4}\].
Suy ra tọa độ \(A\left( {\frac{3}{4};0} \right)\).
Trục Oy: x = 0.
Với x = 0, ta có: y = –4.0 + 3 = 3.
Suy ra tọa độ B(0; 3).
Vậy \(A\left( {\frac{3}{4};0} \right)\), B(0; 3) thỏa mãn yêu cầu bài toán.
c) Gọi H là chân đường vuông góc kẻ từ O đến đường thẳng d.
Ta có \(OA = \frac{3}{4},\,\,OB = 3\).
Tam giác OAB vuông tại O có OH là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{{{{\left( {\frac{3}{4}} \right)}^2}}} + \frac{1}{{{3^2}}} = \frac{{17}}{9}\).
Suy ra \(O{H^2} = \frac{9}{{17}}\).
Do đó \(OH = \frac{3}{{\sqrt {17} }}\).
Vậy khoảng cách từ gốc tọa độ đến d bằng \(\frac{3}{{\sqrt {17} }}\).
d) Ta có \({S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.\frac{3}{4}.3 = \frac{9}{8}\).
Vậy diện tích tam giác OAB là \(\frac{9}{8}\).
Câu 7:
Tính tổng sau: 300 – (–200) – (–120) + 18.
 Xem đáp án
Xem đáp án
Ta có: 300 – (–200) – (–120) + 18.
= (300 + 200) + (120 + 18).
= 500 + 138.
= 638.
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
 Xem đáp án
Xem đáp án
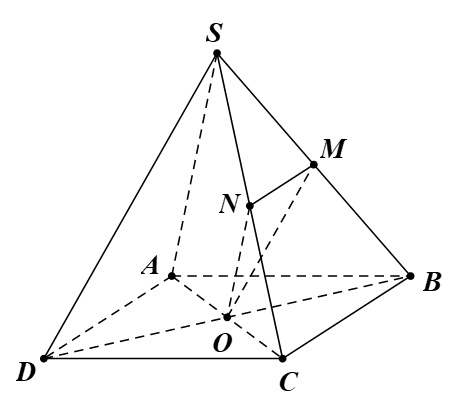
Ta có \(\frac{{d\left( {O,\left( {BCNM} \right)} \right)}}{{d\left( {A,\left( {BCNM} \right)} \right)}} = \frac{{CO}}{{CA}} = \frac{1}{2}\) (do O là trung điểm AC).
\( \Rightarrow d\left( {O,\left( {BCNM} \right)} \right) = \frac{1}{2}d\left( {A,\left( {BCNM} \right)} \right)\).
Lại có \({S_{SMN}} = \frac{1}{2}SM.SN.\sin \widehat {MSN} = \frac{1}{8}SB.SC.\sin \widehat {MSN} = \frac{1}{4}{S_{SBC}}\).
Suy ra \({S_{BCNM}} = {S_{SBC}} - {S_{SMN}} = {S_{SBC}} - \frac{1}{4}{S_{SBC}} = \frac{3}{4}{S_{SBC}}\).
Ta có \({S_{ABC}} = \frac{1}{2}d\left( {A,CD} \right).CD\) và SABCD = d(A, CD).CD.
Suy ra \({S_{ABC}} = \frac{1}{2}{S_{ABCD}}\).
Vì vậy \({V_{O.BCNM}} = \frac{1}{3}d\left( {O,\left( {BCNM} \right)} \right).{S_{BCNM}} = \frac{1}{3}.\frac{1}{2}d\left( {A,\left( {BCNM} \right)} \right).\frac{3}{4}{S_{SBC}}\).
\( = \frac{3}{8}{V_{SABC}} = \frac{3}{8}.\frac{1}{3}d\left( {S,\left( {ABC} \right)} \right).{S_{ABC}} = \frac{3}{8}.\frac{1}{3}d\left( {S,\left( {ABCD} \right)} \right).\frac{1}{2}{S_{ABCD}} = \frac{3}{{16}}{V_{S.ABCD}}\).
Suy ra \(\frac{{{V_{O.BCNM}}}}{{{V_{S.ABCD}}}} = \frac{3}{{16}}\).
Vậy tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD là \(\frac{3}{{16}}\).
Câu 9:
Cung lồi, cung lõm và điểm uốn là gì?
 Xem đáp án
Xem đáp án
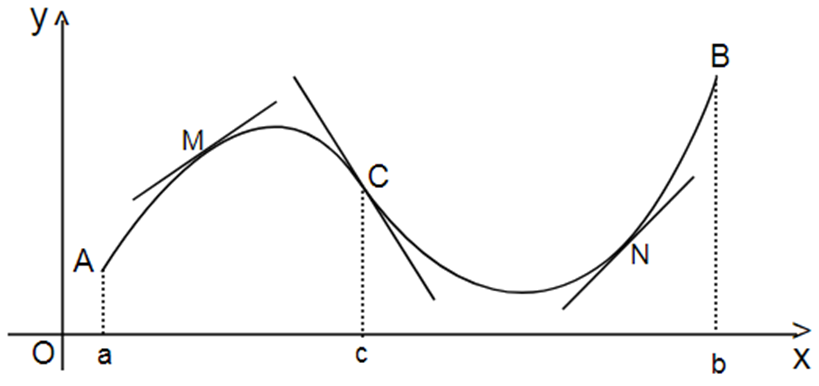
+ Cung lồi: Tại mọi điểm của cung AC, tiếp tuyến luôn nằm bên trên cung, khi đó ta nói cung AC là một cung lồi. Khoảng [a; c] ứng với cung lồi AC gọi là khoảng lồi của đồ thị (với a là hoành độ điểm A, c là hoành độ điểm C).
+ Cung lõm: Trên cung CB, mọi tiếp tuyến đều nằm dưới đồ thị, khi đó CB được gọi là cung lõm và đoạn [c; b] là khoảng lõm của đồ thị.
+ Điểm uốn: Điểm chuyển tiếp giữa cung lồi và cung lõm (từ lồi chuyển sang lõm hoặc từ lõm chuyển sang lồi) gọi là điểm uốn của đồ thị. Trong đồ thị trên, điểm C là điểm uốn.
Câu 10:
Tìm giá trị nhỏ nhất: \(A = \sqrt {4{x^2} - 4x + 1} + \sqrt {4{x^2} - 12x + 9} \).
 Xem đáp án
Xem đáp án
Ta có \(A = \sqrt {4{x^2} - 4x + 1} + \sqrt {4{x^2} - 12x + 9} \).
\( = \sqrt {{{\left( {2x - 1} \right)}^2}} + \sqrt {{{\left( {2x - 3} \right)}^2}} \).
= |2x – 1| + |2x – 3|.
= |2x – 1| + |3 – 2x|.
Áp dụng công thức |A| + |B| ≥ |A + B|, ta có:
|2x – 1| + |3 – 2x| ≥ |2x – 1 + 3 – 2x| = |2| = 2.
Vậy giá trị nhỏ nhất của A bằng 2.
Câu 11:
Mẹ hơn con 30 tuổi, tuổi mẹ gấp 6 lần tuổi con. Hỏi tuổi của mỗi người?
 Xem đáp án
Xem đáp án
Tuổi mẹ là 6 phần, tuổi con là 1 phần.
Hiệu số phần bằng nhau là:
6 – 1 = 5 (phần).
Giá trị của một phần là:
30 : 5 = 6 (tuổi).
Tuổi con là:
6 × 1 = 6 (tuổi).
Tuổi mẹ là:
6 × 6 = 36 (tuổi).
Đáp số: Tuổi mẹ: 36 tuổi;
Tuổi con: 6 tuổi.
Câu 12:
Tìm tất cả các nghiệm nguyên dương của phương trình 6x2 + 5y2 = 74.
 Xem đáp án
Xem đáp án
Ta có 6x2 + 5y2 = 74.
⇔ 6(x2 – 4) = 5(10 – y2) (1)
Từ (1), ta suy ra 6(x2 – 4) ⋮ 5 và (6; 5) = 1.
⇒ x2 – 4 ⋮ 5.
⇒ x2 = 5k + 4 (k ∈ ℕ).
Thay x2 – 4 = 5k vào (1) ta được: 30k = 5(10 – y2).
⇒ 6k = 10 – y2.
⇒ y2 = 10 – 6k.
Ta có \(\left\{ \begin{array}{l}{x^2} > 0\\{y^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5k + 4 > 0\\10 - 6k > 0\end{array} \right.\)
\( \Leftrightarrow - \frac{4}{5} < k < \frac{5}{3}\).
Mà k ∈ ℕ.
Do đó ta nhận k ∈ {0; 1}.
Với k = 0, ta có y2 = 10. Suy ra \(y = \pm \sqrt {10} \) (loại vì y nguyên dương).
Với k = 1, ta có \(\left\{ \begin{array}{l}{x^2} = 5k + 4 = 5.1 + 4 = 9\\{y^2} = 10 - 6k = 10 - 6.1 = 4\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}x = \pm 3\\y = \pm 2\end{array} \right.\)
Vì x, y nguyên dương nên ta nhận x = 3, y = 2.
Vậy (x, y) ∈ {(3; 2)} thỏa mãn yêu cầu bài toán.
Câu 13:
Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz. Tìm giá trị lớn nhất của biểu thức \(P = \frac{1}{{\sqrt {1 + {x^2}} }} + \frac{1}{{\sqrt {1 + {y^2}} }} + \frac{1}{{\sqrt {1 + {z^2}} }}\).
 Xem đáp án
Xem đáp án
Ta có x + y + z = xyz.
\( \Leftrightarrow x = \frac{{x + y + z}}{{yz}}\).
\( \Leftrightarrow {x^2} = \frac{{{x^2} + xy + xz}}{{yz}}\).
\( \Leftrightarrow {x^2} + 1 = \frac{{\left( {x + y} \right)\left( {x + z} \right)}}{{yz}}\).
\( \Rightarrow \frac{1}{{\sqrt {{x^2} + 1} }} = \sqrt {\frac{{yz}}{{\left( {x + y} \right)\left( {x + z} \right)}}} \).
Chứng minh tương tự, ta có \(\frac{1}{{\sqrt {{y^2} + 1} }} = \sqrt {\frac{{xz}}{{\left( {x + y} \right)\left( {y + z} \right)}}} \); \(\frac{1}{{\sqrt {{z^2} + 1} }} = \sqrt {\frac{{xy}}{{\left( {x + z} \right)\left( {y + z} \right)}}} \).
Cộng theo từng vế ba đẳng thức trên và áp dụng bất đẳng thức Cauchy, ta được:
\(P = \frac{1}{{\sqrt {1 + {x^2}} }} + \frac{1}{{\sqrt {1 + {y^2}} }} + \frac{1}{{\sqrt {1 + {z^2}} }}\)
\( = \sqrt {\frac{{yz}}{{\left( {x + y} \right)\left( {x + z} \right)}}} + \sqrt {\frac{{xz}}{{\left( {x + y} \right)\left( {y + z} \right)}}} + \sqrt {\frac{{xy}}{{\left( {x + z} \right)\left( {y + z} \right)}}} \)
\( \le \frac{1}{2}\left( {\frac{y}{{x + y}} + \frac{z}{{x + z}}} \right) + \frac{1}{2}\left( {\frac{x}{{x + y}} + \frac{z}{{y + z}}} \right) + \frac{1}{2}\left( {\frac{x}{{x + z}} + \frac{y}{{y + z}}} \right)\)
\( = \frac{1}{2}\left( {\frac{y}{{x + y}} + \frac{z}{{x + z}} + \frac{x}{{x + y}} + \frac{z}{{y + z}} + \frac{x}{{x + z}} + \frac{y}{{y + z}}} \right)\)
\( = \frac{3}{2}\).
Dấu “=” xảy ra \( \Leftrightarrow x = y = z = \sqrt 3 \).
Vậy giá trị lớn nhất của biểu thức P bằng \(\frac{3}{2}\) khi và chỉ khi \(x = y = z = \sqrt 3 \).
Câu 14:
Cho hàm số y = f(x) = (5 – 3a)x + a + 6.
a) Với giá trị nào của a thì hàm số đồng biến, nghịch biến?
b) Biết f(–2) = 10. Tính f(2).
c) Biết f(3) = 5, hàm số đã cho đồng biến hay nghịch biến?
 Xem đáp án
Xem đáp án
a) Hàm số đã cho đồng biến ⇔ 5 – 3a > 0.
\[ \Leftrightarrow a < \frac{5}{3}\].
Hàm số đã cho nghịch biến ⇔ 5 – 3a < 0.
\[ \Leftrightarrow a > \frac{5}{3}\].
Vậy \[a < \frac{5}{3}\] thì hàm số đã cho đồng biến; \[a > \frac{5}{3}\] thì hàm số đã cho nghịch biến.
b) Ta có f(–2) = 10.
⇔ (5 – 3a).(–2) + a + 6 = 10.
⇔ –10 + 6a + a + 6 = 10.
⇔ 7a = 14.
⇔ a = 2.
Khi đó ta có hàm số y = f(x) = –x + 8.
Vậy f(2) = –2 + 8 = 6.
c) Với f(3) = 5, ta có: (5 – 3a).3 + a + 6 = 5.
⇔ 15 – 9a + a + 6 = 5.
⇔ 8a = 16.
⇔ a = 2.
Vì \[a = 2 > \frac{5}{3}\] nên hàm số đã cho nghịch biến khi f(3) = 5.
Câu 15:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết rằng AB = a, \(AD = a\sqrt 3 \) và \(\widehat {ASB} = 60^\circ \). Tính diện tích khối cầu ngoại tiếp hình chóp S.ABCD.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
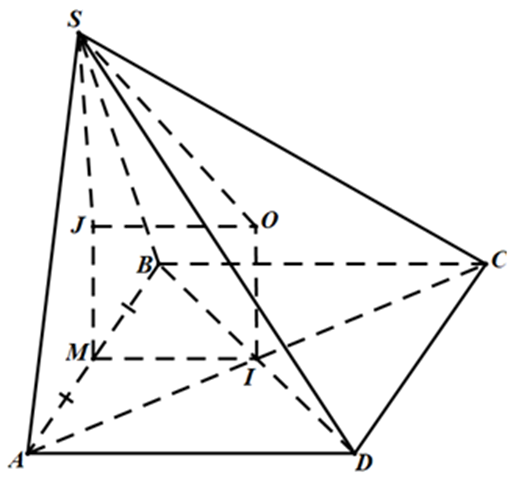
Gọi I, J lần lượt là tâm đường tròn ngoại tiếp hình chữ nhật ABCD và tam giác SAB.
Gọi M là trung điểm của AB và O là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có JM ⊥ AB và IM ⊥ AB.
Mà (SAB) ⊥ (ABCD).
Do đó IM ⊥ JM (1)
Ta có O là tâm của mặt cầu ngoại tiếp hình chóp.
Suy ra OI ⊥ (ABCD).
Do đó OI ⊥ IM (2)
Ta có O là tâm của mặt cầu ngoại tiếp hình chóp.
Suy ra OJ ⊥ (SAB).
Do đó OJ ⊥ JM (3)
Từ (1), (2), (3), suy ra bốn điểm O, J, M, I đồng phẳng và tứ giác OJMI là hình chữ nhật (do có 3 góc ở đỉnh là góc vuông).
Gọi R, Rb lần lượt là bán kính mặt cầu ngoại tiếp khối chóp S.ABCD và bán kính đường tròn ngoại tiếp tam giác SAB.
Áp dụng định lí Pytago, ta được: \(I{A^2} = \frac{{A{C^2}}}{4} = \frac{{B{D^2}}}{4} = \frac{{A{B^2} + A{D^2}}}{4} = \frac{{{a^2} + 3{a^2}}}{4} = {a^2}\).
Áp dụng định lí sin trong tam giác SAB, ta được: \({R_b} = \frac{{AB}}{{2\sin \widehat {ASB}}} = \frac{a}{{2.\sin 60^\circ }} = \frac{{a\sqrt 3 }}{3}\).
Ta có \(R = SO = \sqrt {S{J^2} + O{J^2}} = \sqrt {R_b^2 + I{M^2}} = \sqrt {R_b^2 + I{A^2} - A{M^2}} \).
\( = \sqrt {R_b^2 + I{A^2} - \frac{{A{B^2}}}{4}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2} + {a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt {39} }}{6}\).
Vậy diện tích khối cầu ngoại tiếp hình chóp S.ABCD là: \(S = 4\pi {R^2} = \frac{{13\pi {a^2}}}{3}\).
Do đó ta chọn phương án B.
Câu 16:
Tính \(\frac{{a - x}}{{6{x^2} - ax - 2{a^2}}} - \frac{{a + x}}{{4{a^2} - 4ax - 3{x^2}}}\).
 Xem đáp án
Xem đáp án
Ta xét mẫu của phân số thứ nhất:
6x2 – ax – 2a2 = 6x2 + 3ax – 4ax – 2a2
= 3x(2x + a) – 2a(2x + a)
= (2x + a)(3x – 2a).
Ta xét mẫu của phân số thứ hai:
4a2 – 4ax – 3x2 = 4a2 + 2ax – 6ax – 3x2
= 2a(2a + x) – 3x(2a + x)
= (2a + x)(2a – 3x).
Khi đó ta có \(\frac{{a - x}}{{6{x^2} - ax - 2{a^2}}} - \frac{{a + x}}{{4{a^2} - 4ax - 3{x^2}}}\).
\( = \frac{{a - x}}{{\left( {2x + a} \right)\left( {3x - 2a} \right)}} - \frac{{a + x}}{{\left( {2a + x} \right)\left( {2a - 3x} \right)}}\).
\( = \frac{{a - x}}{{\left( {2x + a} \right)\left( {3x - 2a} \right)}} + \frac{{a + x}}{{\left( {2a + x} \right)\left( {3x - 2a} \right)}}\).
\[ = \frac{{\left( {a - x} \right)\left( {2a + x} \right) + \left( {a + x} \right)\left( {2x + a} \right)}}{{\left( {2x + a} \right)\left( {3x - 2a} \right)\left( {2a + x} \right)}}\].
\[ = \frac{{2{a^2} - ax - {x^2} + 3ax + {a^2} + 2{x^2}}}{{\left( {2x + a} \right)\left( {3x - 2a} \right)\left( {2a + x} \right)}}\].
\[ = \frac{{3{a^2} + 2ax + {x^2}}}{{\left( {2x + a} \right)\left( {3x - 2a} \right)\left( {2a + x} \right)}}\].
Vậy \(\frac{{a - x}}{{6{x^2} - ax - 2{a^2}}} - \frac{{a + x}}{{4{a^2} - 4ax - 3{x^2}}} = \frac{{3{a^2} + 2ax + {x^2}}}{{\left( {2x + a} \right)\left( {3x - 2a} \right)\left( {2a + x} \right)}}\).
Câu 17:
Cho tam giác ABC vuông tại A, AB = 3 và AC = 4. Gọi I là tâm đường tròn nội tiếp của tam giác ABC. Chứng minh rằng \(5\overrightarrow {IA} + 4\overrightarrow {IB} + 3\overrightarrow {IC} = \vec 0\).
 Xem đáp án
Xem đáp án
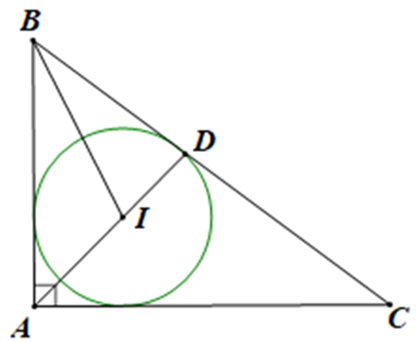
Do tam giác ABC vuông tại A nên BC2 = AB2 + AC2 (Định lí Pythagore).
Suy ra \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\).
Gọi AD là đường phân giác của tam giác ABC.
Áp dụng tính chất đường phân giác, ta được: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{3}{4}\).
Khi đó \(\overrightarrow {BD} = \frac{3}{4}\overrightarrow {DC} \).
\( \Leftrightarrow \overrightarrow {ID} - \overrightarrow {IB} = \frac{3}{4}\overrightarrow {IC} - \frac{3}{4}\overrightarrow {ID} \).
\( \Leftrightarrow \frac{7}{4}\overrightarrow {ID} = \overrightarrow {IB} + \frac{3}{4}\overrightarrow {IC} \).
\( \Leftrightarrow 7\overrightarrow {ID} = 4\overrightarrow {IB} + 3\overrightarrow {IC} \) (1)
Lại có BI là đường phân giác của tam giác ABD (do I là tâm đường tròn ngoại tiếp tam giác ABC).
Áp dụng tính chất đường phân giác, ta được: \(\frac{{ID}}{{IA}} = \frac{{BD}}{{BA}} = \frac{{DC}}{{AC}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{{ID}}{{IA}} = \frac{{BD}}{{BA}} = \frac{{DC}}{{AC}} = \frac{{BD + DC}}{{BA + AC}} = \frac{{BC}}{{BA + AC}} = \frac{5}{7}\).
Khi đó \(7\overrightarrow {ID} = - 5\overrightarrow {IA} \) (2)
Từ (1), (2), suy ra \(4\overrightarrow {IB} + 3\overrightarrow {IC} = - 5\overrightarrow {IA} \).
Vậy \(5\overrightarrow {IA} + 4\overrightarrow {IB} + 3\overrightarrow {IC} = \vec 0\) (điều phải chứng minh).
Câu 18:
Vẽ \[\widehat {xOy} = 50^\circ \]. Lấy điểm M thuộc Ox sao cho OM = 6 cm. Vẽ đường thẳng d là trung trực của đoạn thẳng OM.
 Xem đáp án
Xem đáp án
– Vẽ \[\widehat {xOy} = 50^\circ \].
– Lấy điểm M thuộc Ox sao cho OM = 6 cm.
– Lấy điểm N là trung điểm của đoạn ON, tức là ON = 3 cm.
– Vẽ đường thẳng d đi qua N là vuông góc với OM.
Khi đó d là đường trung trực của đoạn thẳng OM.
Ta được hình vẽ sau:

Câu 19:
Tính giá trị của biểu thức A = (x – 3)2 – (x + 1)3 + 12x(x – 1), với \(x = - \frac{1}{2}\).
 Xem đáp án
Xem đáp án
Ta có A = (x – 3)2 – (x + 1)3 + 12x(x – 1).
= x2 – 6x + 9 – (x3 + 1 + 3x2 + 3x) + 12x2 – 12x.
= –x3 + 10x2 – 21x + 8.
Thế \(x = - \frac{1}{2}\) vào A, ta được: \(A = - {\left( { - \frac{1}{2}} \right)^3} + 10.{\left( { - \frac{1}{2}} \right)^2} - 21.\left( { - \frac{1}{2}} \right) + 8 = \frac{{169}}{8}\).
Vậy \(A = \frac{{169}}{8}\) khi \(x = - \frac{1}{2}\).
Câu 20:
Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \(AM = \frac{{AC}}{4}\). Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
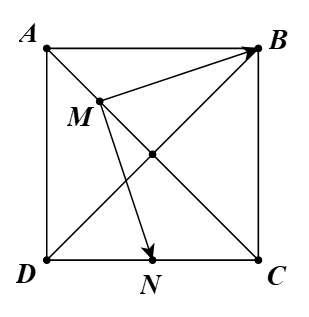
Ta phân tích các vectơ \(\overrightarrow {MB} ,\,\,\overrightarrow {MN} \) theo các vectơ có giá vuông góc với nhau.
⦁ \(\overrightarrow {MB} = \overrightarrow {AB} - \overrightarrow {AM} = \overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} = \overrightarrow {AB} - \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AD} \).
⦁ \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {DN} - \frac{1}{4}\overrightarrow {AC} = \overrightarrow {AD} + \frac{1}{2}\overrightarrow {DC} - \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\).
\( = \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} - \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{3}{4}\overrightarrow {AD} + \frac{1}{4}\overrightarrow {AB} \).
Khi đó \(\overrightarrow {MB} .\overrightarrow {MN} = \frac{1}{4}\left( {3\overrightarrow {AB} - \overrightarrow {AD} } \right)\left( {\overrightarrow {AB} + 3\overrightarrow {AD} } \right) = \frac{1}{4}\left( {3A{B^2} + 8\overrightarrow {AB} .\overrightarrow {AD} - 3A{D^2}} \right)\)
\( = \frac{1}{4}\left( {{{3.2}^2} + 8.0 - {{3.2}^2}} \right) = 0\).
Vậy ta chọn phương án B.
Câu 21:
Cho \(\cos a = \frac{4}{5}\) và 0° < a < 90°. Tính sina, tana, cota.
 Xem đáp án
Xem đáp án
⦁ Ta có \({\sin ^2}a = 1 - {\cos ^2}a = 1 - {\left( {\frac{4}{5}} \right)^2} = \frac{9}{{25}}\).
\( \Rightarrow \sin a = \pm \frac{3}{5}\).
Vì 0° < a < 90° nên sina > 0.
Do đó \(\sin a = \frac{3}{5}\).
⦁ Ta có \(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{3}{5}:\frac{4}{5} = \frac{3}{4}\).
⦁ Ta có \(\cot a = \frac{1}{{\tan a}} = \frac{4}{3}\).
Vậy \(\sin a = \frac{3}{5}\); \(\tan a = \frac{3}{4}\) và \(\cot a = \frac{4}{3}\).
Câu 22:
Hình thang ABCD (AB // CD) có M, N, P, Q theo thứ tự là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
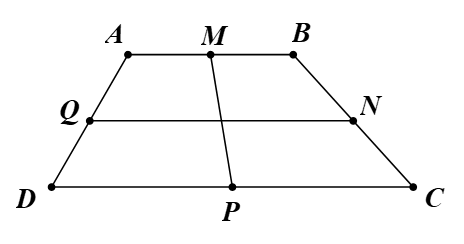
Ta có N, Q lần lượt là trung điểm của BC, DA.
Suy ra NQ là đường trung bình của hình thang ABCD.
Do đó NQ // AB // CD và \(NQ = \frac{{AB + CD}}{2}\).
Vậy ta chọn phương án D.
Câu 23:
Có bao nhiêu số tự nhiên có 5 chữ số khác nhau, biết rằng có đúng 3 chữ số chẵn và 2 chữ số lẻ còn lại đứng kề nhau?
 Xem đáp án
Xem đáp án
Chọn 2 chữ số lẻ từ 5 chữ số lẻ và có sắp xếp thứ tự thì có \(A_5^2\) cách.
Chọn 3 chữ số chẵn từ 5 chữ số chẵn thì có \(C_5^3\) cách.
Chọn 3 chữ số chẵn từ 5 chữ số chẵn, trong đó có mặt chữ số 0 thì có \(C_4^2\) cách.
Coi 2 chữ số lẻ là 1 chữ số, kết hợp với 3 chữ số chẵn ta được 4 “chữ số”, sau đó sắp xếp thứ tự chúng thì có 4! cách.
Trường hợp chữ số 0 đứng đầu thì có 3! cách.
Vậy số các số thỏa mãn yêu cầu bài toán là: \(A_5^2.\left( {C_5^3.4! - C_4^2.3!} \right) = 4080\) (số).
Câu 24:
Gọi m0 là giá trị thực của tham số m để parabol (P): y = x2 – 2x + 3 – m cắt trục hoành Ox tại hai điểm phân biệt A, B sao cho độ dài đoạn thẳng AB bằng 4. Tìm m0.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (P) và trục Ox là: x2 – 2x + 3 – m = 0 (1)
∆’ = 1 – 3 + m = m – 2.
Ta có parabol (P) cắt trục Ox tại hai điểm A, B phân biệt.
⇔ Phương trình (1) có 2 nghiệm phân biệt.
⇔ ∆’ > 0.
⇔ m > 2 (*)
Hai nghiệm là: \(\left[ \begin{array}{l}{x_A} = 1 + \sqrt {m - 2} \\{x_B} = 1 - \sqrt {m - 2} \end{array} \right.\)
Khi đó ta có tọa độ giao điểm \[A\left( {1 + \sqrt {m - 2} ;0} \right),\,\,B\left( {1 - \sqrt {m - 2} ;0} \right)\].
Theo đề, ta có \(AB = 2\sqrt {m - 2} = 2\).
\( \Leftrightarrow \sqrt {m - 2} = 1\).
⇔ m – 2 = 1.
⇔ m = 3.
So với (*), nhận m = 3.
Vậy m0 = 3 thỏa mãn yêu cầu bài toán.
Câu 25:
Tính \(C_{2021}^1 + C_{2021}^2 + C_{2021}^3\).
 Xem đáp án
Xem đáp án
Ta có \(C_{2021}^1 + C_{2021}^2 + C_{2021}^3 = \frac{{2021!}}{{1!.2020!}} + \frac{{2021!}}{{2!.2019!}} + \frac{{2021!}}{{3!.2018!}}\).
\( = 2021!.\left( {\frac{1}{{2020.2019.2018!}} + \frac{1}{{2.2019.2018!}} + \frac{1}{{6.2018!}}} \right)\).
\( = \frac{{2021.2020.2019.2018!}}{{2018!}}.\left( {\frac{1}{{2020.2019}} + \frac{1}{{2.2019}} + \frac{1}{6}} \right)\).
\( = 2021.2020.2019.\left[ {\frac{1}{{2019}}\left( {\frac{1}{{2020}} + \frac{1}{2}} \right) + \frac{1}{6}} \right]\).
\[ = 2021.2020.2019.\left( {\frac{1}{{2019}}.\frac{{1011}}{{2020}} + \frac{1}{6}} \right)\].
\[ = 2021.1011 + \frac{{2021.1010.2.3.673}}{6}\].
= 2021.1011 + 2021.1010.673.
= 2021.(1011 + 679 730).
= 2021.680 741.
= 1 375 777 561.
Câu 26:
Với các số 0, 1, 3, 6, 9, có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau và không chia hết cho 3.
 Xem đáp án
Xem đáp án
Gọi \(\overline {abcd} \) là số tự nhiên có 4 chữ số khác nhau được lập từ các chữ số 0, 1, 3, 6, 9.
Ta có:
⦁ a có 4 cách chọn (a ≠ 0).
⦁ b có 4 cách chọn.
⦁ c có 3 cách chọn.
⦁ d có 2 cách chọn.
Suy ra ta có tất cả 4.4.3.2 = 96 số tự nhiên có 4 chữ số khác nhau.
Ta thấy các số có 4 chữ số khác nhau và chia hết cho 3 được lập từ các số 0, 3, 6, 9.
Gọi \(\overline {mnpq} \) là số tự nhiên có 4 chữ số khác nhau và chia hết cho 3 được lập từ các số 0, 3, 6, 9.
Khi đó:
⦁ m có 3 cách chọn (m ≠ 0).
⦁ n có 3 cách chọn.
⦁ p có 2 cách chọn.
⦁ q có 1 cách chọn.
Suy ra ta có tất cả 3.3.2.1 = 18 số tự nhiên 4 chữ số khác nhau và chia hết cho 3 được lập từ các số 0, 1, 3, 6, 9.
Vậy ta có tất cả 96 – 18 = 78 số thỏa mãn yêu cầu bài toán.
Câu 27:
Hỏi phương trình 3x2 – 6x + ln(x + 1)3 + 1 = 0 có bao nhiêu nghiệm phân biệt?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Điều kiện: x > –1.
Ta có 3x2 – 6x + ln(x + 1)3 + 1 = 0.
⇔ 3x2 – 6x + 3ln(x + 1) + 1 = 0.
Đặt f(x) = 3x2 – 6x + 3ln(x + 1) + 1.
Suy ra \(f'\left( x \right) = 6x - 6 + \frac{3}{{x + 1}}\).
Cho \(f'\left( x \right) = 0 \Leftrightarrow 6x - 6 + \frac{3}{{x + 1}} = 0\).
⇔ 6(x – 1)(x + 1) + 3 = 0.
⇔ 2x2 – 1 = 0.
\( \Leftrightarrow x = \pm \frac{{\sqrt 2 }}{2}\).
Bảng biến thiên:
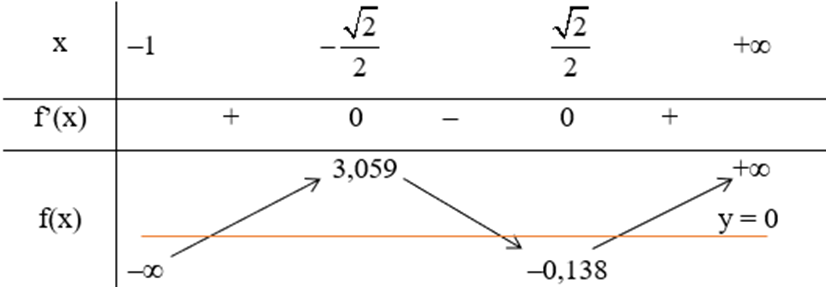
Quan sát bảng biến thiên, ta thấy đồ thị hàm số y = f(x) cắt đường thẳng y = 0 tại 3 điểm phân biệt.
Do đó phương trình f(x) = 0 có 3 nghiệm phân biệt.
Vậy ta chọn phương án C.
Câu 28:
Cho 6 điểm A, B, C, D, E, F phân biệt. Chứng minh
\(\overrightarrow {AD} + \overrightarrow {CE} + \overrightarrow {DC} = \overrightarrow {AB} - \overrightarrow {EB} \).
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AD} + \overrightarrow {CE} + \overrightarrow {DC} = \overrightarrow {AB} - \overrightarrow {EB} \).
\( \Leftrightarrow \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CE} = \overrightarrow {AB} + \overrightarrow {BE} \).
\( \Leftrightarrow \overrightarrow {AC} + \overrightarrow {CE} = \overrightarrow {AE} \).
\( \Leftrightarrow \overrightarrow {AE} = \overrightarrow {AE} \) (đúng).
Vậy ta có điều phải chứng minh.
Câu 29:
Cho hàm số bậc nhất y = (m – 1)x + 4. Tìm m để đồ thị hàm số cắt 2 trục tọa độ tại hai điểm A, B phân biệt thỏa mãn diện tích tam giác AOB bằng 24.
 Xem đáp án
Xem đáp án
Điều kiện: m ≠ 1.
Trục Ox: y = 0.
Trục Oy: x = 0.
Với y = 0, ta có: \(0 = \left( {m - 1} \right)x + 4 \Leftrightarrow x = \frac{{ - 4}}{{m - 1}}\).
Suy ra tọa độ \(A\left( {\frac{{ - 4}}{{m - 1}};0} \right)\).
Với x = 0, ta có: y = (m – 1).0 + 4 = 0.
Suy ra tọa độ B(0; 4).
Ta có \(OA = \left| {\frac{{ - 4}}{{m - 1}}} \right| = \frac{4}{{\left| {m - 1} \right|}}\), OB = 4.
Khi đó \({S_{\Delta AOB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{4}{{\left| {m - 1} \right|}}.4 = \frac{8}{{\left| {m - 1} \right|}}\).
Theo đề, ta có diện tích tam giác AOB bằng 24.
\( \Leftrightarrow \frac{8}{{\left| {m - 1} \right|}} = 24\).\( \Leftrightarrow \left| {m - 1} \right| = \frac{1}{3}\).
\( \Leftrightarrow \left[ \begin{array}{l}m - 1 = \frac{1}{3}\\m - 1 = - \frac{1}{3}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m = \frac{4}{3}\\m = \frac{2}{3}\end{array} \right.\)
So với điều kiện m ≠ 1, ta nhận \(\left[ \begin{array}{l}m = \frac{4}{3}\\m = \frac{2}{3}\end{array} \right.\).
Vậy \(\left[ \begin{array}{l}m = \frac{4}{3}\\m = \frac{2}{3}\end{array} \right.\) thỏa mãn yêu cầu bài toán.
Câu 30:
Cho tam giác ABC với A(2; 3), B(–1; 4), C(1; 1). Tìm tọa độ đỉnh D của hình bình hành:
a) ABCD.
b) ACBD.
 Xem đáp án
Xem đáp án
a) Ta có \(\overrightarrow {AB} = \left( { - 3;1} \right)\), \(\overrightarrow {DC} = \left( {1 - {x_D};1 - {y_D}} \right)\).
Vì ABCD là hình bình hành nên ta có \(\overrightarrow {AB} = \overrightarrow {DC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}1 - {x_D} = - 3\\1 - {y_D} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 4\\{y_D} = 0\end{array} \right.\)
Vậy tọa độ D(4; 0) thỏa mãn yêu cầu bài toán.
b) Ta có \(\overrightarrow {AC} = \left( { - 1; - 2} \right)\), \(\overrightarrow {DB} = \left( { - 1 - {x_D};4 - {y_D}} \right)\).
Vì ACBD là hình bình hành nên ta có \(\overrightarrow {AC} = \overrightarrow {DB} \).
\( \Leftrightarrow \left\{ \begin{array}{l} - 1 - {x_D} = - 1\\4 - {y_D} = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = 6\end{array} \right.\)
Vậy tọa độ D(0; 6) thỏa mãn yêu cầu bài toán.
Câu 31:
Cho tam giác ABC đều cạnh bằng a, M là điểm di động trên đường thẳng AC. Tìm giá trị nhỏ nhất của biểu thức \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} } \right|\).
 Xem đáp án
Xem đáp án
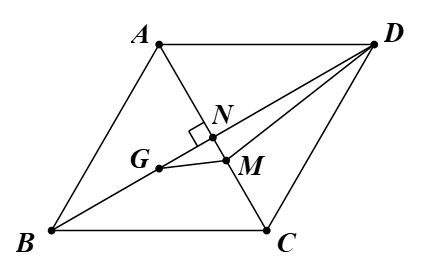
Gọi G là trọng tâm của tam giác ABC, N là trung điểm của AC.
Suy ra ba điểm B, G, N thẳng hàng.
Dựng hình bình hành ABCD.
Khi đó trung điểm N của AC cũng là trung điểm của đoạn BD.
Ta có \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} } \right|\)
\( = \left| {3\overrightarrow {MG} } \right| + 3\left| {\overrightarrow {BA} + \overrightarrow {MC} } \right|\)
\( = 3MG + 3\left| {\overrightarrow {CD} + \overrightarrow {MC} } \right|\)
\( = 3MG + 3\left| {\overrightarrow {MD} } \right|\)
= 3(MG + MD) ≥ 3GD (theo bất đẳng thức tam giác).
Dấu “=” xảy ra ⇔ M là giao điểm của GD và AC hay M là trung điểm của AC.
Khi đó M trùng N.
Vì tam giác ABC đều nên đường trung tuyến BN cũng là đường cao của tam giác ABC.
Tam giác ABN vuông tại N: \(BN = \sqrt {A{B^2} - A{N^2}} = \sqrt {A{B^2} - \frac{{A{C^2}}}{4}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\).
Khi đó \(GN = \frac{1}{3}BN = \frac{{a\sqrt 3 }}{6}\) và \(ND = BN = \frac{{a\sqrt 3 }}{2}\).
Vì vậy \(3GD = 3\left( {GN + ND} \right) = 3\left( {\frac{{a\sqrt 3 }}{6} + \frac{{a\sqrt 3 }}{2}} \right) = 2a\sqrt 3 \).
Vậy \({T_{\min }} = 2a\sqrt 3 \) khi M là trung điểm của AC.
Câu 32:
Tính giá trị của biểu thức D = (3x + 5)(2x – 1) + (4x – 1)(3x + 2), với |x| = 2.
 Xem đáp án
Xem đáp án
Ta có D = (3x + 5)(2x – 1) + (4x – 1)(3x + 2)
= 6x2 – 3x + 10x – 5 + 12x2 + 8x – 3x – 2
= 18x2 + 12x – 7.
Theo đề, ta có \(\left| x \right| = 2 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Thay x = 2 vào D, ta được: D = 18.22 + 12.2 – 7 = 89.
Thay x = –2 vào D, ta được: D = 18.(–2)2 + 12.(–2) – 7 = 41.
Vậy D = 89 hoặc D = 41 khi |x| = 2.
Câu 33:
Cho hàm số \(y = f\left( x \right) = \frac{{12}}{x}\).
a) Tính f(5) và f(–3).
b) Hãy điền giá trị tương ứng của hàm số vào bảng sau:
|
x |
6 |
4 |
3 |
2 |
5 |
8 |
12 |
|
\(f\left( x \right) = \frac{{12}}{x}\) |
? |
? |
? |
? |
? |
? |
? |
 Xem đáp án
Xem đáp án
a) Thế x = 5 vào hàm số \(f\left( x \right) = \frac{{12}}{x}\), ta được: \(f\left( 5 \right) = \frac{{12}}{5}\).
Thế x = –3 vào hàm số \(f\left( x \right) = \frac{{12}}{x}\), ta được: \(f\left( { - 3} \right) = \frac{{12}}{{ - 3}} = - 4\).
Vậy \(f\left( 5 \right) = \frac{{12}}{5}\) và f(–3) = –4.
b) Thực hiện tương tự câu a với các giá trị của x trong bảng, ta thu được bảng sau:
|
x |
6 |
4 |
3 |
2 |
5 |
8 |
12 |
|
\(f\left( x \right) = \frac{{12}}{x}\) |
2 |
3 |
4 |
6 |
\(\frac{{12}}{5}\) |
\(\frac{3}{2}\) |
1 |
Câu 34:
Với a, b, c là các số thực không âm thỏa mãn a + b + c = 2. Tìm giá trị lớn nhất của P = a + 2b2 + 3c3.
 Xem đáp án
Xem đáp án
Vì a, b, c không âm và a + b + c = 2 nên 0 ≤ a, b, c ≤ 2.
Khi đó ta có:
⦁ a ≤ 12a;
⦁ 2b2 = 2b.b ≤ 4b ≤ 12b;
⦁ 3c3 = 3c2.c ≤ 3.22.c = 12c.
Suy ra P = a + 2b2 + 3c3 ≤ 12(a + b + c) = 12.2 = 24.
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = 0\\c = 2\end{array} \right.\).
Vậy Pmax = 24 khi (a; b; c) = (0; 0; 2).
Câu 35:
Cho hình chữ nhật ABCD có AB = 4 cm, BC = 3 cm. Kẻ BH vuông góc với AC tại H, tia BH cắt AD ở E.
1) Tính AC, BH, \(\widehat {BAC}\).
2) Chứng minh BH.BE = CD2.
3) Kẻ EF vuông góc với BC tại F. Chứng minh .
4) Tính diện tích tam giác BHF.
 Xem đáp án
Xem đáp án
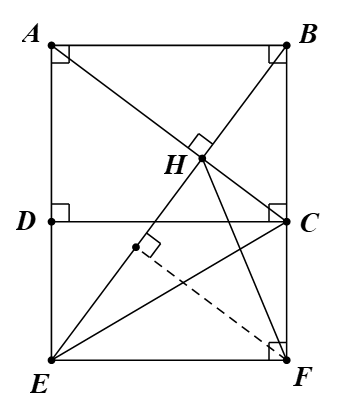
1) Tam giác ABC vuông tại B (do ABCD là hình chữ nhật) có BH là đường cao:
⦁ AC2 = AB2 + BC2 (Định lí Pythagore).
= 42 + 32 = 25.
Suy ra AC = 5 (cm).
⦁ \(\frac{1}{{B{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\) (Hệ thức lượng trong tam giác vuông).
\( = \frac{1}{{{4^2}}} + \frac{1}{{{3^2}}} = \frac{{25}}{{144}}\).
Suy ra \(B{H^2} = \frac{{144}}{{25}}\).
Khi đó \(BH = \frac{{12}}{5}\) (cm).
⦁ \(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{3}{4}\). Suy ra \(\widehat {BAC} \approx 36^\circ 52'\).
Vậy AC = 5 cm; \(BH = \frac{{12}}{5}\) cm và \(\widehat {BAC} \approx 36^\circ 52'\).
2) Ta có AB = CD (do ABCD là hình chữ nhật).
Tam giác ABE vuông tại A có AH là đường cao:
AB2 = BH.BE (Hệ thức lượng trong tam giác vuông).
Vậy BH.BE = CD2 (điều phải chứng minh).
3) Xét ∆BHC và ∆BFE, có:
\(\widehat {HBC}\) chung;
\(\widehat {BHC} = \widehat {BFE} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{BH}}{{BF}} = \frac{{BC}}{{BE}}\).
Xét ∆BHF và ∆BCE, có:
\(\widehat {HBC}\) chung;
\(\frac{{BH}}{{BC}} = \frac{{BF}}{{BE}}\) (do \(\frac{{BH}}{{BF}} = \frac{{BC}}{{BE}}\)).
Vậy (c.g.c).
4) Ta có CDEF là hình chữ nhật (do \(\widehat {CDE} = \widehat {DCF} = \widehat {CFE} = 90^\circ \)).
Suy ra EF = CD = AB = 4 (cm).
Vì \(\frac{{BH}}{{BF}} = \frac{{BC}}{{BE}}\) nên BC.BF = BH.BE = CD2 = AB2 = 16 (cm).
Suy ra \(BF = \frac{{16}}{{BC}} = \frac{{16}}{3}\) (cm).
Khi đó \({S_{\Delta BFE}} = \frac{1}{2}BF.EF = \frac{1}{2}.\frac{{16}}{3}.4 = \frac{{32}}{3}\) (cm2).
Tam giác BFE vuông tại F: BE2 = BF2 + EF2 (Định lí Pythagore).
Suy ra \[BE = \sqrt {B{F^2} + E{F^2}} = \sqrt {{{\left( {\frac{{16}}{3}} \right)}^2} + {4^2}} = \frac{{20}}{3}\] (cm).
Ta thấy tam giác BEF và tam giác BHF có chung đường cao hạ từ điểm F.
Suy ra \(\frac{{{S_{\Delta BHF}}}}{{{S_{\Delta BEF}}}} = \frac{{BH}}{{BE}} = \frac{{12}}{5}:\frac{{20}}{3} = \frac{9}{{25}}\).
Vậy \({S_{\Delta BHF}} = \frac{9}{{25}}.{S_{\Delta BEF}} = \frac{9}{{25}}.\frac{{32}}{3} = \frac{{96}}{{25}}\) (cm2).
Câu 36:
Cho hình bình hành ABCD có \(\widehat A = 120^\circ \). Tia phân giác của \(\widehat D\) qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:
a) AB = 2AD.
b) DI = 2AH.
c) AC vuông góc với AD.
 Xem đáp án
Xem đáp án

a) Hình bình hành ABCD có \(\widehat {BAD},\,\widehat {ADC}\) ở vị trí trong cùng phía.
Suy ra \(\widehat {ADC} = 180^\circ - \widehat {BAD} = 60^\circ \).
Khi đó \(\widehat {ADI} = \widehat {IDC} = \frac{{\widehat {ADC}}}{2} = 30^\circ \) (do DI là tia phân giác của \(\widehat {ADC}\)).
Mà \(\widehat {AID} = \widehat {IDC}\) (cặp góc so le trong).
Vì vậy \(\widehat {AID} = \widehat {ADI}\).
Suy ra tam giác ADI cân tại A.
Do đó AD = AI.
Mà AB = 2AI (I là trung điểm của AB).
Vậy AB = 2AD (điều phải chứng minh).
b) Gọi J là trung điểm của DI.
Tam giác ADI có AJ là đường trung tuyến.
Suy ra AJ vừa là đường phân giác, vừa là đường cao của tam giác ADI.
Khi đó \(\widehat {JAI} = \widehat {DAJ} = \frac{{\widehat {DAI}}}{2} = 60^\circ \).
Xét ∆AJD và ∆DHA, có:
\(\widehat {AJD} = \widehat {DHA} = 90^\circ \);
AD là cạnh chung;
\(\widehat {DAJ} = \widehat {ADH} = 60^\circ \).
Do đó ∆AJD = ∆DHA (cạnh huyền – góc nhọn).
Suy ra DJ = AH (cặp cạnh tương ứng).
Mà DI = 2DJ (J là trung điểm của DI).
Vậy DI = 2AH (điều phải chứng minh).
c) Ta có BI = BC \(\left( { = \frac{1}{2}AB} \right)\).
Suy ra tam giác IBC cân tại B.
Mà \(\widehat {IBC} = \widehat {ADC} = 60^\circ \).
Do đó tam giác IBC đều.
Vì vậy IC = IB = IA.
Khi đó tam giác ABC vuông tại C hay \(\widehat {ACB} = 90^\circ \).
Suy ra \(\widehat {DAC} = \widehat {ACB} = 90^\circ \).
Vậy AD ⊥ AC (điều phải chứng minh).
Câu 37:
Tổng của ba số bằng 13,68. Biết rằng tổng của số thứ nhất và số thứ hai bằng 5,79; tổng của số thứ hai và số thứ ba bằng 12,45. Tìm ba số đó.
 Xem đáp án
Xem đáp án
Số thứ ba là: 13,68 – 5,79 = 7,89.
Số thứ hai là: 12,45 – 7,89 = 4,56.
Số thứ nhất là: 5,79 – 4,56 = 1,23.
Đáp số: Số thứ nhất: 1,23;
Số thứ hai: 4,56;
Số thứ ba: 7,89.
Câu 38:
Giải phương trình: x2 + x – 1 = 0.
 Xem đáp án
Xem đáp án
Ta có x2 + x – 1 = 0.
∆ = 12 – 4.1.(–1) = 5 > 0.
Do đó phương trình đã cho có 2 nghiệm phân biệt.
Hai nghiệm là: \(\left[ \begin{array}{l}{x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}} = \frac{{ - 1 + \sqrt 5 }}{2}\\{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}} = \frac{{ - 1 - \sqrt 5 }}{2}\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ {\frac{{ - 1 \pm \sqrt 5 }}{2}} \right\}\).
Câu 39:
Tìm x, biết: x : 0,25 + x × 11 = 24.
 Xem đáp án
Xem đáp án
Ta có x : 0,25 + x × 11 = 24
x × 4 + x × 11 = 24
x × (4 + 11) = 24
x × 15 = 24
x = 24 : 15
x = 1,6
Vậy x = 1,6.
Câu 40:
Cho a, b, c là các số hữu tỉ khác 0 thỏa mãn a + b + c = 0. Chứng minh rằng: \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\) là bình phương của một số hữu tỉ.
 Xem đáp án
Xem đáp án
Ta có \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = {\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)^2} - 2\left( {\frac{1}{{ab}} + \frac{1}{{bc}} + \frac{1}{{ca}}} \right)\)
\( = {\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)^2} - 2.\frac{{c + a + b}}{{abc}} = {\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)^2} - 2.\frac{0}{{abc}} = {\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)^2}\).
Vậy ta có điều phải chứng minh.
Câu 41:
Cho đường tròn (O; R) và điểm A cố định nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
c) Chứng minh tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
 Xem đáp án
Xem đáp án
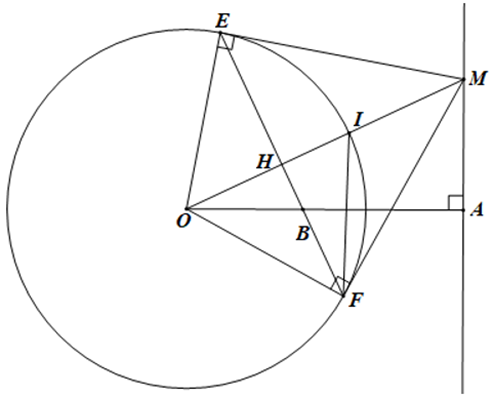
a) Do ME, MF là hai tiếp tuyến của (O) nên ME = MF.
Khi đó M thuộc đường trung trực của đoạn EF (1)
Lại có OE = OF = R.
Suy ra O thuộc đường trung trực của đoạn EF (2)
Từ (1), (2), suy ra OM là đường trung trực của đoạn EF.
Do đó OM ⊥ EF.
Ta có \[\widehat {MHB} + \widehat {MAB} = 90^\circ + 90^\circ = 180^\circ \].
Vậy tứ giác ABHM nội tiếp đường tròn đường kính MB.
b) Xét ∆OHB và ∆OAM, có:
\(\widehat {HOB}\) chung;
\(\widehat {OHB} = \widehat {OAM} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{OH}}{{OA}} = \frac{{OB}}{{OM}}\).
Vì vậy OH.OM = OA.OB (3)
Tam giác OEM vuông tại E có EH là đường cao:
OE2 = OH.OM (Hệ thức lượng trong tam giác vuông).
⇔ R2 = OH.OM (4)
Từ (3), (4), ta thu được OA.OB = OH.OM = R2.
c) Gọi I là giao điểm của OM với đường tròn (O).
Ta có \(\widehat {MFI} = \widehat {FEI}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung FI) (5)
Do EF ⊥ OM nên .
Suy ra \(\widehat {FEI} = \widehat {EFI}\) (hai góc nội tiếp chắn hai cung bằng nhau) (6)
Từ (5), (6), suy ra \(\widehat {MFI} = \widehat {EFI}\).
Do đó FI là tia phân giác của \(\widehat {MFE}\).
Tam giác MEF cân tại M có MH là đường trung trực.
Suy ra MH cũng là đường phân giác của tam giác MEF.
Ta có I là giao điểm của hai đường phân giác FI, MH của tam giác MEF.
Khi đó I là tâm của đường tròn nội tiếp tam giác MEF.
Mà I thuộc đường tròn (O) cố định.
Vậy ta có điều phải chứng minh.
d) Ta có \({S_{\Delta HBO}} = \frac{1}{2}OH.HB\).
Ta có (chứng minh trên).
Suy ra \(\frac{{HB}}{{AM}} = \frac{{OB}}{{OM}}\).
Do đó HB.OM = AM.OB (7)
Lại có OH.OM = R2 (kết quả câu b) (8)
Nhân (7) và (8) vế theo vế, ta được: \(OH.HB.O{M^2} = {R^2}.AM.OB = {R^2}.AM.\frac{{{R^2}}}{{OA}}\).
\( \Rightarrow OH.HB = AM.\frac{{{R^4}}}{{OA.O{M^2}}} = {R^4}.\frac{{AM}}{{OA.\left( {O{A^2} + A{M^2}} \right)}}\).
Áp dụng bất đẳng thức Cauchy, ta được: OA2 + AM2 ≥ 2OA.AM.
Khi đó ta có \(OH.HB = {R^4}.\frac{{AM}}{{OA.\left( {O{A^2} + A{M^2}} \right)}} \le {R^4}.\frac{{AM}}{{OA.2.OA.AM}} = \frac{{{R^4}}}{{2O{A^2}}}\).
Suy ra \({S_{\Delta HBO}} \le \frac{{{R^4}}}{{4O{A^2}}}\).
Dấu “=” xảy ra ⇔ OA = AM.
Vì vậy diện tích tam giác HBO lớn nhất bằng \(\frac{{{R^4}}}{{4O{A^2}}}\) khi và chỉ khi OA = OM.
Vậy M là điểm nằm trên đường thẳng d sao cho OA = OM thì diện tích tam giác HBO lớn nhất.
Câu 42:
Trong vườn có 12 cây cam và 28 cây chanh. Tìm tỉ số phần trăm số cây cam so với tổng số cây trong vườn.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trong vườn có tổng số cây là:
12 + 28 = 40 (cây)
Tỉ số phần trăm của cây cam so với tổng số cây trong vườn là:
12 : 40 = 0,3 = 30%
Đáp số: 30%.
Câu 43:
Cho biểu thức \(P = \left( {\frac{{x - 3\sqrt x }}{{x - 9}} - 1} \right):\left( {\frac{{9 - x}}{{x + \sqrt x - 6}} - \frac{{\sqrt x - 3}}{{2 - \sqrt x }} - \frac{{\sqrt x - 2}}{{\sqrt x + 3}}} \right)\).
a) Rút gọn P.
b) Tìm giá trị của x để P < 1.
 Xem đáp án
Xem đáp án
a) ĐKXĐ: \(\left\{ \begin{array}{l}x \ne 9\\x \ne 4\\x \ge 0\end{array} \right.\) (*)
\(P = \left( {\frac{{x - 3\sqrt x }}{{x - 9}} - 1} \right):\left( {\frac{{9 - x}}{{x + \sqrt x - 6}} - \frac{{\sqrt x - 3}}{{2 - \sqrt x }} - \frac{{\sqrt x - 2}}{{\sqrt x + 3}}} \right)\)
\[ = \left[ {\frac{{\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - 1} \right]:\left[ {\frac{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 3} \right)}} + \frac{{\sqrt x - 3}}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 3}}} \right]\]
\[ = \left( {\frac{{\sqrt x }}{{\sqrt x + 3}} - 1} \right):\left( {\frac{{3 - \sqrt x }}{{\sqrt x - 2}} + \frac{{\sqrt x - 3}}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 3}}} \right)\]
\[ = \frac{{\sqrt x - \sqrt x - 3}}{{\sqrt x + 3}}:\left( {\frac{{3 - \sqrt x + \sqrt x - 3}}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 3}}} \right)\]
\[ = \frac{{ - 3}}{{\sqrt x + 3}}:\left( { - \frac{{\sqrt x - 2}}{{\sqrt x + 3}}} \right)\]
\[ = \frac{{ - 3}}{{\sqrt x + 3}}.\frac{{\sqrt x + 3}}{{2 - \sqrt x }}\]
\[ = \frac{3}{{\sqrt x - 2}}\].
b) Ta có \(P < 1 \Leftrightarrow \frac{3}{{\sqrt x - 2}} < 1\).
\( \Leftrightarrow \frac{{3 - \sqrt x + 2}}{{\sqrt x - 2}} < 0\).
\( \Leftrightarrow \frac{{5 - \sqrt x }}{{\sqrt x - 2}} < 0\).
\( \Leftrightarrow \left\{ \begin{array}{l}5 - \sqrt x < 0\\\sqrt x - 2 > 0\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}5 - \sqrt x > 0\\\sqrt x - 2 < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\sqrt x > 5\\\sqrt x > 2\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}\sqrt x < 5\\\sqrt x < 2\end{array} \right.\)
\( \Leftrightarrow \sqrt x > 5\) hoặc \(\sqrt x < 2\).
⇔ x > 25 hoặc x < 4.
So với điều kiện (*), ta nhận x > 25 hoặc 0 ≤ x < 4.
Vậy x > 25 hoặc 0 ≤ x < 4 thỏa mãn yêu cầu bài toán.
Câu 44:
Hãy so sánh: 2565 và 318.
 Xem đáp án
Xem đáp án
Ta có 2565 = (28)5 =28.5 = (25)8 = 328.
Vì 31 < 32 nên 318 < 328.
Vậy 318 < 2565.
Câu 45:
Cho (O; R), đường kính AB và một điểm M nằm trên (O; R) với MA < MB (M khác A và B). Tiếp tuyến tại M của (O; R) cắt tiếp tuyến tại A, B của (O; R) lần lượt tại C và D.
a) Chứng minh rằng ABDC là hình thang vuông.
b) AD cắt (O; R) tại E, OD cắt MB tại N. Chứng minh rằng OD vuông góc với MB và DE.DA = DN.DO.
c) Đường thẳng vuông góc với AB tại O cắt đường thẳng AM tại F. Chứng tỏ OFDB là hình chữ nhật.
d) AM = R. Tính diện tích tứ giác ACDB theo R.
 Xem đáp án
Xem đáp án
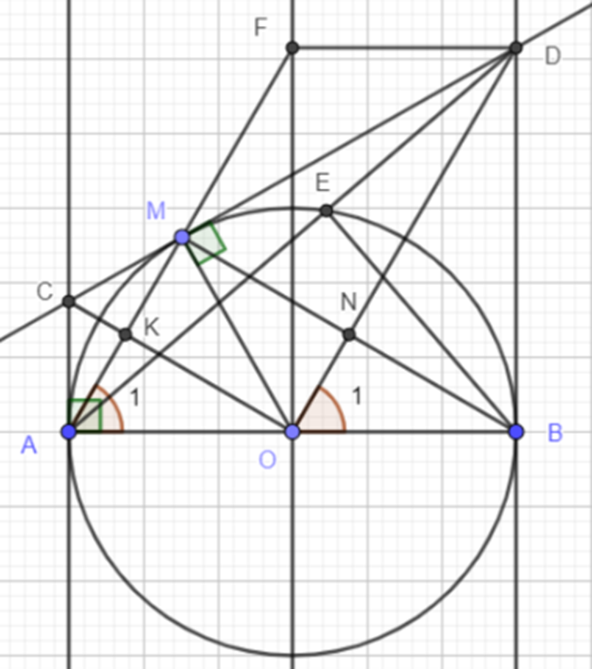
a) Ta có AC là tiếp tuyến của (O). Suy ra AC ⊥ AB (1)
Chứng minh tương tự, ta được BD ⊥ AB (2)
Từ (1), (2), suy ra AC // BD và \[\widehat {BAC} = 90^\circ \].
Vậy ABDC là hình thang vuông.
b) Ta có MD, MB là hai tiếp tuyến của (O).
Suy ra MD = MB.
Do đó D thuộc đường trung trực của đoạn MB (3)
Lại có OB = OM = R.
Suy ra O thuộc đường trung trực của đoạn MB (4)
Từ (3), (4), suy ra OD là đường trung trực của đoạn MB.
Vậy OD ⊥ MB tại N.
Ta có \(\widehat {AEB} = 90^\circ \) và \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O)).
Tam giác ABD vuông tại B có BE là đường cao: BD2 = DE.DA (5)
Tam giác BDO vuông tại B có BN là đường cao: BD2 = DN.DO (6)
Từ (5), (6), ta thu được DE.DA = DN.DO.
c) Xét ∆AOF và ∆OBD, có:
\(\widehat {AOF} = \widehat {OBD} = 90^\circ \);
AO = OB (= R);
\(\widehat {{A_1}} = \widehat {{O_1}}\) (cùng phụ với \(\widehat {ABM}\)).
Do đó ∆AOF = ∆OBD (cạnh huyền – góc nhọn).
Suy ra OF = BD (cặp cạnh tương ứng).
Mà OF // BD (cùng vuông góc với AB).
Do đó OFDB là hình bình hành.
Mà \[\widehat {OBD} = 90^\circ \].
Vậy OFDB là hình chữ nhật.
d) Ta có AM = OM = OA = R.
Suy ra tam giác OAM đều.
Do đó \(\widehat {DBM} = \widehat {{A_1}} = 60^\circ \) (cùng phụ với \(\widehat {ABM}\)) và DM = DB (tính chất hai tiếp tuyến cắt nhau).
Suy ra tam giác MBD đều.
Khi đó DB = MB.
Tam giác ABM vuông tại M: \[MB = \sqrt {A{B^2} - A{M^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 \].
Ta có CA = CM và CO là tia phân giác của \(\widehat {ACM}\) (tính chất hai tiếp tuyến cắt nhau).
Suy ra tam giác ACM cân tại C có CO là vừa là đường phân giác, vừa là đường cao.
Gọi K là giao điểm của CO và AM. Suy ra K là trung điểm của AM và CK ⊥ AK.
Ta có \(\widehat {CAK} = 90^\circ - \widehat {KAO} = 90^\circ - 60^\circ = 30^\circ \).
Tam giác AKC vuông tại K: \[AC = \frac{{AK}}{{\cos \widehat {CAK}}} = \frac{{AM}}{{2.\cos \widehat {CAK}}} = \frac{R}{{2.\cos 30^\circ }} = \frac{R}{{\sqrt 3 }}\].
Khi đó \[{S_{ABDC}} = \frac{{\left( {AC + BD} \right).AB}}{2} = \frac{{\left( {AC + MB} \right).AB}}{2}\].
\[ = \frac{{\left( {\frac{R}{{\sqrt 3 }} + R\sqrt 3 } \right).2R}}{2} = \frac{{4{R^2}}}{{\sqrt 3 }}\].
Vậy diện tích tứ giác ABDC bằng \[\frac{{4{R^2}}}{{\sqrt 3 }}\].
Câu 46:
Viết phương trình đường thẳng (d) song song với đường thẳng (d1): y = –2x + 5 và đi qua điểm A(–2; 1).
 Xem đáp án
Xem đáp án
Vì (d) // (d1) nên phương trình đường thẳng (d) có dạng: y = –2x + b (b ≠ 5).
Ta có (d) đi qua điểm A(–2; 1). Suy ra 1 = –2.(–2) + b.
Khi đó b = –3 (nhận).
Vậy phương trình (d): y = –2x – 3.
