 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
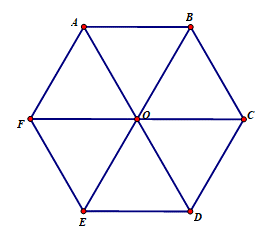
Với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau), ta có thể xếp chúng thành hình lục giác đều với các đường chéo chính cắt nhau như hình trên, ta được 6 hình tam giác đều.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
Cho định lí “Cho số tự nhiên n, nếu n5 chia hết cho 5 thì n chia hết cho 5”.
Định lí này được viết dưới dạng P Þ Q. Hãy phát biểu định lí đảo của định lí trên rồi dùng các thuật ngữ “điều kiện cần và đủ” phát biểu gộp cả 2 định lí thuận và đảo.