Tìm các khoảng đồng biến, nghịch biến của các hàm số:
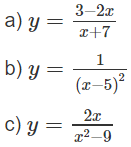
Giải bởi Vietjack
a) TXĐ: R \ {-7}
y' < 0 trên các khoảng (-∞; -7), (-7; +∞) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R \ {5}
y' < 0 trên khoảng (5; +∞) nên y nghịch biến trên khoảng (5; +∞)
y' > 0 trên khoảng (-∞; 5) nên y đồng biến trên khoảng (-∞; 5)
c) TXĐ: R \ {-3; 3}
y' < 0 trên các khoảng (-∞; - 3), (-3; 3), (3; +∞) nên hàm số đã cho nghịch biến trên các khoảng đó.
d) TXĐ: R \ {0}
y' = 0 ⇔ 
Bảng biến thiên:
Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)
e) TXĐ: R \ {-1}
y' = 0 ⇔ 
Vậy hàm số đã cho đồng biến trên các khoảng (−∞; −1 − √6), (−1 + √6; +∞) và nghịch biến trên các khoảng (−1 − √6; −1),(−1; −1 + √6)
g) TXĐ: R \ {2}
(do x2 − 4x + 7x2 − 4x + 7 có Δ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (−∞;2),(2;+∞)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3x2 − 8x3
b) y = 16x + 2x2 − 16x3/3 − x4
c) y = x3 − 6x2 + 9x
d) y = x4 + 8x2 + 5
Xác định giá trị của b để hàm số f(x) = sinx – bx + c nghịch biến trên toàn trục số.
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b) 
với 0 < x < +∞
Chứng minh các phương trình sau có nghiệm duy nhất
3(cosx − 1) + 2sinx + 6x = 0
Xác định tham số m để hàm số sau:
a)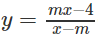 
đồng biến trên từng khoảng xác định;
b) y = −x3 + mx2 − 3x + 4 nghịch biến trên.
Tìm giá trị của tham số m để các hàm số y = x3 - 2mx2 + 12x - 7 đồng biến trên R.
Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định
