Phương trình nào sau đây có nghiệm duy nhất trên R?
A.
B.
C.
D.
Giải bởi Vietjack
Đáp án: C
Vì f'(x) = (x5 + x3 - 7)' = 5x4 + 3x2 ≥ 0, ∀x ∈ R (dấu "=" xảy ra ⇔ x = 0). Suy ra f(x) đồng biến trên R. Mặt khác f(0) = -7, f(2) = 32 + 8 - 7 = 33 > 0. Hàm f(x) liên tục trên đoạn [0;2] nên tồn tại x0 ∈ (0;2) để f(x0) = 0. Suy ra f(x) = 0 có nghiệm duy nhất trên R.
Cách khác: Phương trình 3sin2x - cos2x + 5 = 0
⇔ 3sin2x + sin2x + 4 = 4(sin2x + 1) = 0, vô nghiệm
Các phương trình x2 - 5x + 6 = 0 và 3tanx - 4 = 0 có nhiều hơn một nghiệm. Từ đó suy ra phương trình x5 + x3 - 7 = 0 có nghiệm duy nhất trên R.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3x2 − 8x3
b) y = 16x + 2x2 − 16x3/3 − x4
c) y = x3 − 6x2 + 9x
d) y = x4 + 8x2 + 5
Xác định giá trị của b để hàm số f(x) = sinx – bx + c nghịch biến trên toàn trục số.
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b) 
với 0 < x < +∞
Chứng minh các phương trình sau có nghiệm duy nhất
3(cosx − 1) + 2sinx + 6x = 0
Xác định tham số m để hàm số sau:
a)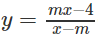 
đồng biến trên từng khoảng xác định;
b) y = −x3 + mx2 − 3x + 4 nghịch biến trên.
Tìm giá trị của tham số m để các hàm số y = x3 - 2mx2 + 12x - 7 đồng biến trên R.
Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định
