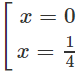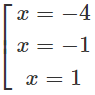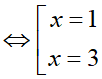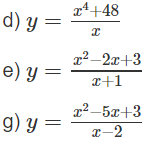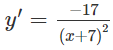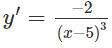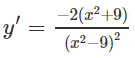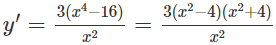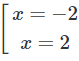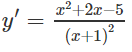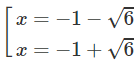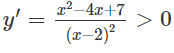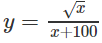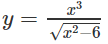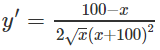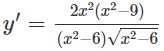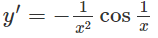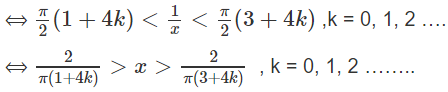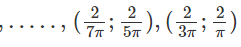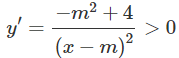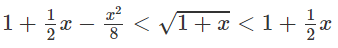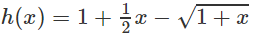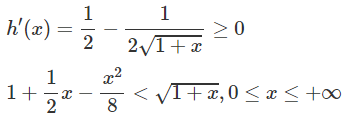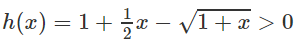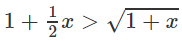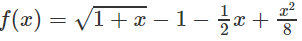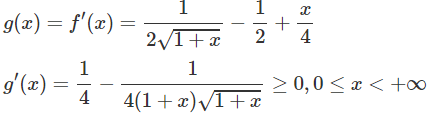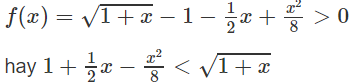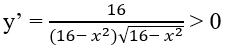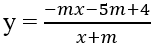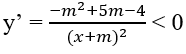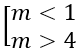Giải SBT Toán 12 Giải tích - Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Giải sbt Giải tích 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
-
1082 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3x2 − 8x3
b) y = 16x + 2x2 − 16x3/3 − x4
c) y = x3 − 6x2 + 9x
d) y = x4 + 8x2 + 5
 Xem đáp án
Xem đáp án
a) TXĐ: R
y′ = 6x − 24x2 = 6x(1 − 4x)
y' = 0 ⇔
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng (-∞; 0 ); (14; +∞), suy ra y nghịch biến trên các khoảng (-∞;0 ); (14;+∞)
b) TXĐ: R
y′ = 16 + 4x − 16x2 − 4x3 = −4(x + 4)(x2 − 1)
y' = 0 ⇔
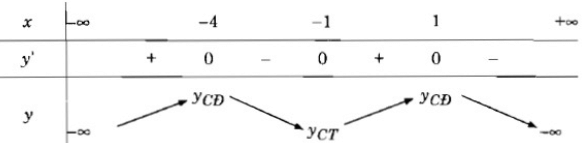
Bảng biến thiên:
Vậy hàm số y đã cho đồng biến trên các khoảng (-∞; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; +∞)
c) TXĐ: R
y′ = 3x2 − 12x + 9
y' = 0
y' > 0 trên các khoảng (-∞; 1), (3; +∞) nên y đồng biến trên các khoảng (-∞; 1), (3; +∞)
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: D = R
y′ = 4x3 + 16x = 4x(x2 + 4)
y' = 0 ⇔ x = 0
y' > 0 trên khoảng (0; +∞) ⇒ y đồng biến trên khoảng (0; +∞)
y' < 0 trên khoảng (-∞; 0) ⇒ y nghịch biến trên khoảng (-∞; 0)
Câu 2:
Tìm các khoảng đồng biến, nghịch biến của các hàm số:
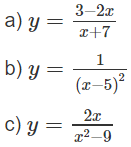
 Xem đáp án
Xem đáp án
a) TXĐ: R \ {-7}
y' < 0 trên các khoảng (-∞; -7), (-7; +∞) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R \ {5}
y' < 0 trên khoảng (5; +∞) nên y nghịch biến trên khoảng (5; +∞)
y' > 0 trên khoảng (-∞; 5) nên y đồng biến trên khoảng (-∞; 5)
c) TXĐ: R \ {-3; 3}
y' < 0 trên các khoảng (-∞; - 3), (-3; 3), (3; +∞) nên hàm số đã cho nghịch biến trên các khoảng đó.
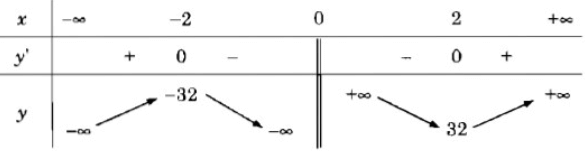
d) TXĐ: R \ {0}
y' = 0 ⇔
Bảng biến thiên:
Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)
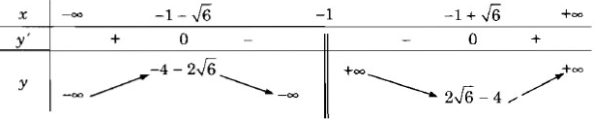
e) TXĐ: R \ {-1}
y' = 0 ⇔
Vậy hàm số đã cho đồng biến trên các khoảng (−∞; −1 − √6), (−1 + √6; +∞) và nghịch biến trên các khoảng (−1 − √6; −1),(−1; −1 + √6)
g) TXĐ: R \ {2}
(do x2 − 4x + 7x2 − 4x + 7 có Δ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (−∞;2),(2;+∞)
Câu 3:
Xét tính đơn điệu của các hàm số sau:
a)
b)
 Xem đáp án
Xem đáp án
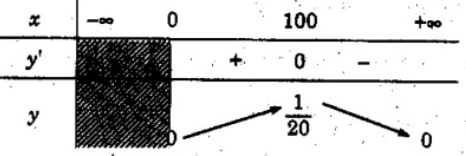
a) TXĐ: [0; +∞)
y’ = 0 ⇔ x = 100
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; +∞)
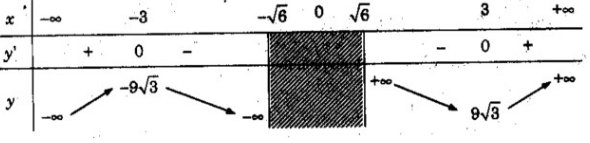
b) TXĐ: (-∞; √6) ∪ (√6; +∞)
y’ = 0 ⇔ x = 3 hoặc x = -3
Vậy hàm số đồng biến trên các khoảng (-∞; -3), (3; +∞), nghịch biến trên các khoảng (-3; −√6 − 6 ), (√6; 3).
Câu 4:
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
 Xem đáp án
Xem đáp án
a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
Giải bất phương trình sau trên khoảng (0; +∞):
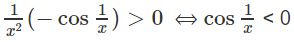
Do đó, hàm số đồng biến trên các khoảng
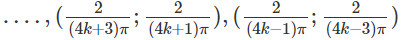
Và nghịch biến trên các khoảng
với k = 0, 1, 2 …
Câu 5:
Xác định tham số m để hàm số sau:
a) 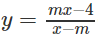
b) y = −x3 + mx2 − 3x + 4 nghịch biến trên.
 Xem đáp án
Xem đáp án
a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng (−∞; m), (m; +∞) khi và chỉ khi:
⇔ − m2 + 4 > 0
⇔ m2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3x2 + 2mx – 3 ≤ 0
⇔ y′ = m2 – 9 ≤ 0
⇔ m2 ≤ 9 ⇔ −3 ≤ m ≤ 3
Câu 6:
Chứng minh các phương trình sau có nghiệm duy nhất
3(cosx − 1) + 2sinx + 6x = 0
 Xem đáp án
Xem đáp án
Đặt y = 3(cos x – 1) + 2sinx + 6
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: y(π) = 0 và y' = -3sin x + 2cos x + 6 > 0, x ∈ R.
Hàm số đồng biến trên R và có một nghiệm x = π
Vậy phương trình đã cho có một nghiệm duy nhất.
Câu 7:
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b)
với 0 < x < +∞
 Xem đáp án
Xem đáp án
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);
x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; +∞)
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; +∞).
Vì h(x) = 0 nên
Hay
Xét hàm số trên f(x) trên [0; +∞);
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; +∞) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
Với mọi 0 < x < +∞.
Câu 8:
Xác định giá trị của b để hàm số f(x) = sinx – bx + c nghịch biến trên toàn trục số.
 Xem đáp án
Xem đáp án
f(x) = sinx – bx + c nghịch biến trên R nếu ta có:
f′(x) = cosx – b ≤ 0, ∀ x ∈ R.
Vì |cosx| ≤ 1| nên f′(x) ≤ 0, ∀ x ∈ R ⇔ b ≥ 1.
Câu 10:
Hàm số 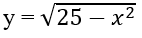
 Xem đáp án
Xem đáp án
Đáp án: C.
Gợi ý: Loại A, D vì tập xác định của hàm số là 25 - x2 ≥ 0 ⇔ -5 ≤ x ≤ 5.
Loại B, vì
| x | -5 | 0 |
| y | 0 | 5 |
Câu 11:
Hàm số 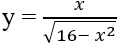
 Xem đáp án
Xem đáp án
Đáp án: B.
Vì
trên tập xác định (-4;4)
Cách khác: Loại A, C, D vì tập xác định của hàm số là (-4;4)
Câu 12:
Phương trình nào sau đây có nghiệm duy nhất trên R?
 Xem đáp án
Xem đáp án
Đáp án: C
Vì f'(x) = (x5 + x3 - 7)' = 5x4 + 3x2 ≥ 0, ∀x ∈ R (dấu "=" xảy ra ⇔ x = 0). Suy ra f(x) đồng biến trên R. Mặt khác f(0) = -7, f(2) = 32 + 8 - 7 = 33 > 0. Hàm f(x) liên tục trên đoạn [0;2] nên tồn tại x0 ∈ (0;2) để f(x0) = 0. Suy ra f(x) = 0 có nghiệm duy nhất trên R.
Cách khác: Phương trình 3sin2x - cos2x + 5 = 0
⇔ 3sin2x + sin2x + 4 = 4(sin2x + 1) = 0, vô nghiệm
Các phương trình x2 - 5x + 6 = 0 và 3tanx - 4 = 0 có nhiều hơn một nghiệm. Từ đó suy ra phương trình x5 + x3 - 7 = 0 có nghiệm duy nhất trên R.
Câu 13:
Phương trình nào sau đây có nghiệm duy nhất trên R?
 Xem đáp án
Xem đáp án
Đáp án: B.
Với f(x) = x3 + 5x + 6 thì vì f'(x) = 3x2 + 5 > 0, ∀x ∈ R nên hàm số f(x) luôn đồng biến trên R. Mặt khác f(-1) = 0. Vậy phương trình f(x) = 0 có nghiệm duy nhất trên R.
Câu 14:
Phương trình nào sau đây có nghiệm duy nhất trên R?
 Xem đáp án
Xem đáp án
Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)(x2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin2x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3π/2.
Câu 15:
Tìm giá trị của tham số m để các hàm số y = x3 - 2mx2 + 12x - 7 đồng biến trên R.
 Xem đáp án
Xem đáp án
Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3x2 - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4m2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.
Câu 16:
Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định
 Xem đáp án
Xem đáp án
Đáp án: A.
Hàm số nghịch biến trên từng khoảng (-∞; -m), (-m; +∞) khi và chỉ khi
⇔ -m2 + 5m - 4 < 0
⇔