25 câu hỏi trắc nghiệm thuộc 150 câu trắc nghiệm Dao động cơ cơ bản (Phần 3)

Câu 1:

Một con lắc lò xo dao động điều hoà với phương trình x = 10cosωt (cm). Tại vị trí có li độ x = 5cm, tỉ số giữa động năng và thế năng của con lắc là:

A. 1.

B. 2.

C. 3

D. 4.

Xem đáp án

Chọn C

=> Tỉ số giữa động năng và thế năng của con lắc là 3.

Câu 2:

Một con lắc lò xo dao động điều hoà đi được 40cm trong thời gian một chu kì dao động. Con lắc có động năng gấp ba lần thế năng tại vị trí có li độ bằng:

A. 20cm

B. ±5cm.

C. ±5 $\sqrt{2}$ cm.

D. $\pm \frac{5}{\sqrt{2}} cm$

Xem đáp án

Chọn B

+ Trong một chu kì vật nặng đi được quãng đường 4A => A = 40 : 4 = 10 cm

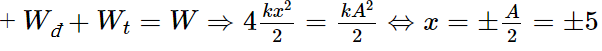
Câu 3:

Một con lắc lò xo gồm một vật nhỏ và lò xo nhẹ có độ cứng 100 N/m. Con lắc dao động đều hòa theo phương ngang với phương trình x = Acos(ωt + φ). Mốc thế năng tại vị trí cân bằng. Khoảng thời gian giữa hai lần liên tiếp con lắc có động năng bằng thế năng là 0,1 s. Lấy π² = 10. Khối lượng vật nhỏ bằng:

A. 40 g.

B. 200 g.

C. 100 g.

D. 400 g.

Xem đáp án

Chọn D

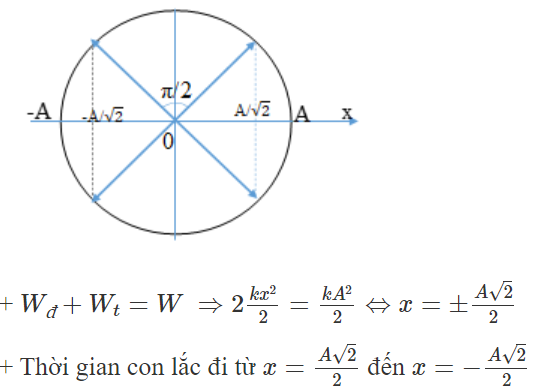
và ngược lại đều bằng T/4

=> T = 4.0,1 = 0,4 (s)

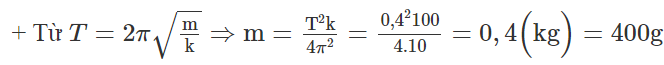
Câu 4:

Con lắc lò xo dao động điều hoà trên phương ngang, lực đàn hồi cực đại tác dụng vào vật bằng 2N và gia tốc cực đại của vật là 2m/s². Khối lượng vật nặng bằng:

A. 1kg.

B. 2kg.

C. 4kg.

D. 100g.

Xem đáp án

Chọn A

+ F_max = ma_max=> m = F_max : a_max = 2 : 2 = 1 (kg).

Câu 5:

Một con lắc lò xo treo thẳng đứng dao động điều hoà với biên độ 4cm, chu kì 0,5s. Khối lượng quả nặng 400g. Lấy g = π²≈ 10m/s². Giá trị cực đại của lực đàn hồi tác dụng vào quả nặng là:

A. 6,56N.

B. 2,56N.

C. 256N.

D. 656N.

Xem đáp án

Chọn A

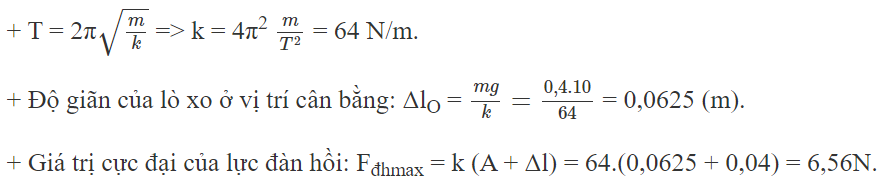
Câu 6:

Một con lắc lò xo dao động điều hoà với biên độ A = 0,1m chu kì dao động T = 0,5s. Khối lượng quả nặng m = 0,25kg. Lực phục hồi cực đại tác dụng lên vật có giá trị:

A. 0,4N.

B. 4N.

C. 10N.

D. 40N.

Xem đáp án

Chọn B

+ ω = $\frac{2 π}{T}$ = 4π rad/s

+ F_phmax = ma_max = mω²A = 0,25.(4π)².0,1 = 4N

Câu 7:

Một con lắc lò xo gồm một quả nặng có khối lượng m = 0,2kg treo vào lò xo có độ cứng k = 100N/m. Cho vật dao động điều hoà theo phương thẳng đứng với biên độ A = 3cm. Lực đàn hồi cực tiểu có giá trị là:

A. 3N.

B. 2N.

C. 1N.

D. 0N.

Xem đáp án

Chọn D

$+ {Δl}_{o} = \frac{mg}{k} = \frac{0, 2.10}{100} = 0, 02 m = 2 cm$ $∆ l_{o} = \frac{m g}{k} = \frac{0, 2.10}{100} = 0, 02 m = 2 c m$

+ Do A = 3cm > Δl_o nên lực đàn hồi cực tiểu có giá trị là 0N.

Câu 8:

Có ba con lắc đơn treo cạnh nhau cùng chiều dài, ba vật bằng sắt, nhôm và gỗ (có khối lượng riêng của sắt > nhôm > gỗ) cùng khối lượng và được phủ mặt ngoài một lớp sơn để lực cản như nhau. Kéo ba vật sao cho ba sợi dây lệch một góc nhỏ như nhau rồi đồng thời buông nhẹ thì:

A. Con lắc bằng gỗ dừng lại sau cùng.

B. Cả ba con lắc dừng cùng một lúc.

C. Con lắc bằng sắt dừng lại sau cùng.

D. Con lắc bằng nhôm dừng lại sau cùng.

Xem đáp án

Chọn C

Năng lượng của con lắc đơn: E =E_{t max}= mgh_max= mgl.(1 - cosa₀)

m = D.V (D là khối lượng riêng của chất làm việc, V là thể thích của vật)

Trong cả 3 con lắc đều có cùng chiều dài l, cùng biên độ góc α₀, cùng thể tích, cùng lực cản nhưng khối lượng riêng của con lắc bằng sắt là lớn nhất, nên cơ năng của nó lớn nhất→ Con lắc bằng sắt dừng lại sau cùng.

Câu 9:

Một con lắc đơn có chiều dài dây treo 1m dao động với biên độ góc nhỏ có chu kì 2s. Cho π = 3,14. Con lắc dao động tại nơi có gia tốc trọng trường là:

A. 9,7 $m / s^{2} .$

B. 10,27 $m / s^{2} .$

C. 10 $m / s^{2} .$

D. 9,86 $m / s^{2} .$

Xem đáp án

Chọn D

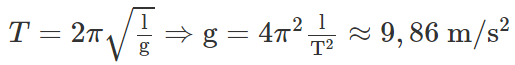
Câu 10:

Một con lắc đơn có độ dài l₁ dao động với chu kì T₁ = 4s. Một con lắc đơn khác có độ dài l₂ dao động tại nơi đó với chu kì T₂ = 3s. Chu kì dao động của con lắc đơn có độ dài l₁ + l₂ là:

A. 5s.

B. 3,5s.

C. 1s.

D. 2,65s.

Xem đáp án

Chọn A

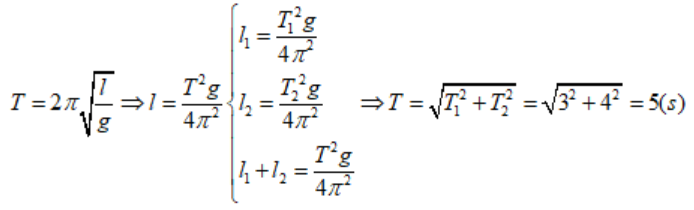
Câu 11:

Hai con lắc đơn có chiều dài lần lượt là l₁ và l₂, tại cùng một vị trí địa lý chúng có chu kỳ tương ứng là T₁ = 3,0s và T₂ = 1,8s. Chu kỳ dao động của con lắc có chiều dài bằng l = l₁ – l₂ sẽ bằng:

A. 1,2s.

B. 2,4s.

C. 4,8s.

D. 2,6.

Xem đáp án

Chọn B

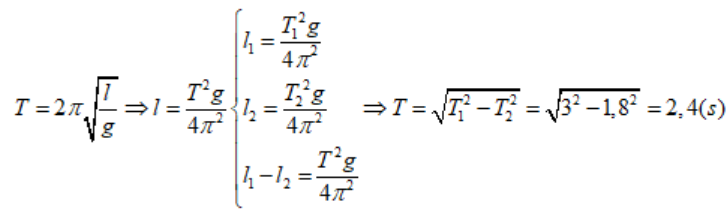
Câu 12:

Tại một nơi, chu kì dao động điều hoà của một con lắc đơn là 2,0 s. Sau khi tăng chiều dài của con lắc thêm 21 cm thì chu kì dao động điều hoà của nó là 2,2 s. Chiều dài ban đầu của con lắc này là:

A. 98 cm.

B. 100 cm.

C. 101 cm.

D. 99 cm.

Xem đáp án

Chọn B

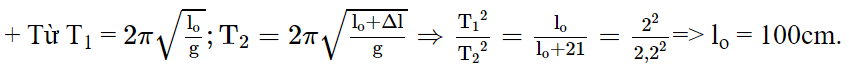
Câu 13:

Con lắc đơn chiều dài l = 16cm. Kéo lệch dây một góc nhỏ rồi buông không vận tốc ban đầu. Khi đi qua vị trí cân bằng, dây gặp một chiếc đinh ở chính giữa chiều dài. Lấy g = π². Chu kỳ dao động của con lắc là:

A. 0,4(s)

B. 0,68(s)

C. 0,28(s)

D. 0,12(s)

Xem đáp án

Chọn B

+ Con lắc dao động ở một bên với thời gian

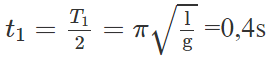
+ Và một bên đối diện con lắc dao động với thời gian

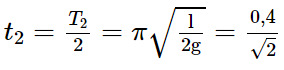
+ Chu kỳ dao động của con lắc là T = t₁ +t₂ ≈ 0,68s.

Câu 14:

Con lắc đơn chiều dài 40cm đang đứng yên ở vị trí cân bằng. Lúc t = 0 truyền cho con lắc vận tốc v₀ = 20cm/s nằm ngang theo chiều dương thì nó dao động điều hoà với chu kì T = 2π/5(s). Phương trình dao động của con lắc dạng li độ góc là:

A. α = 0,1sin( $\frac{t}{5}$ )(rad).

B. α = 0,1sin( $\frac{t}{5}$ + π)(rad).

C. α = 0,1cos(5t- $\frac{π}{2}$ ) (rad).

D. α = 0,1sin(5t + π) (rad).

Xem đáp án

Chọn C

+ ω = $\frac{2 π}{T}$ = 5 (rad/s)

+ v_max = ωA => A = v_max : ω = 0,2 : 5 = 0,04m => α_o = $\frac{A}{l}$ = 0,04/0,4 = 0,1 rad.

+ t = 0: α = 0,1cosφ = 0 và v = -0,5sinφ > 0 => φ = - $\frac{π}{2}$ (rad)

Vậy: $α$ = 0,1cos(5t - $\frac{π}{2}$ ) (rad).

Câu 15:

Một con lắc đơn có chiều dài dây treo 1m dao động điều hòa với biên độ góc π/20 rad tại nơi có gia tốc trọng trường g = 10 m/s². Lấy π² = 10. Thời gian ngắn nhất để con lắc đi từ vị trí cân bằng đến vị trí có li độ góc rad là:

A. 0,5s

B. 3 s

C. 3 $\sqrt{2}$ s

D. $\frac{1}{3}$ s

Xem đáp án

Chọn D

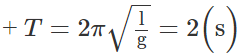
+ Thời gian ngắn nhất để con lắc đi từ vị trí cân bằng đến vị trí có li độ góc $\frac{π 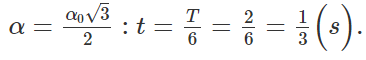\sqrt{3}}{40}$ là đến

Câu 16:

Một con lắc đơn dao động điều hoà với phương trình s = 6cos(0,5πt- $\frac{π}{2}$ )(cm). Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s = 3cm đến li độ cực đại S₀ = 6cm là:

A. $\frac{1}{3}$ s.

B. 4s.

C. $\frac{2}{3}$ s.

D. 1s.

Xem đáp án

Chọn C

$+ T = \frac{2 π}{w} = 4 s$

+ Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s = 3cm đến li độ cực đại S₀ = 6cm: $t = \frac{T}{6} = \frac{4}{6} = \frac{2}{3} s .$

Câu 17:

Một con lắc đơn đang dao động điều hòa với biên độ góc α₀ tại nơi có gia tốc trọng trường là g. Biết lực căng dây lớn nhất bằng 1,02 lần lực căng dây nhỏ nhất. Giá trị của α₀ là:

A. $5, 6^{0}$

B. ${6, 6}^{0}$

C. $3, 3^{0}$

D. $9, 6^{0}$

Xem đáp án

Chọn B

+ Lực căng dây: T = mg(3cosα – 2cosα_o)

=> T_max = mg(3 - 2cosα_o)

T_min = mgcosα_o

+ Ta có: T_max = 1,02 T_min $\Leftrightarrow$ 3 - 2cosα_o= 1,02cosα_o => α_o ≈ 0,1149 rad ≈ 6,6^o.

Câu 18:

Một con lắc đơn có dây treo dài 1m và vật có khối lượng 1kg dao động với biên độ góc 0,1rad. Chọn gốc thế năng tại vị trí cân bằng của vật, lấy g = 10m/s². Cơ năng toàn phần của con lắc là:

A. 0,5J.

B. 0,05J.

C. 0,01J.

D. 0,1J.

Xem đáp án

Chọn B

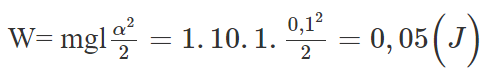
Câu 19:

Chu kì dao động của con lắc đơn là 1s. Thời gian ngắn nhất để con lắc đi từ vị trí mà tại đó động năng cực đại đến vị trí mà tại đó động năng bằng 3 lần thế năng bằng:

A. $\frac{1}{3}$ s.

B. $\frac{2}{13}$ s.

C. $\frac{1}{12}$ s.

D. $\frac{2}{3}$ s.

Xem đáp án

Chọn C

Câu 20:

Một con lắc đơn có l = 1m, dao động điều hòa tại nơi có g = 10m/s² và góc lệch cực đại là 9⁰. Chọn gốc thế tại vị trí cân bằng. Giá trị của vận tốc con lắc tại vị trí động năng bằng thế năng là bao nhiêu?

A. 0,35m/s

B. 0,25m/s

C. 0,4m/s

D. 0,45m/s.

Xem đáp án

Chọn A

+ Động năng bằng thế năng =>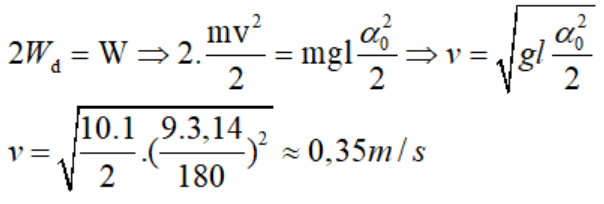

Câu 21:

Một đồng hồ chạy đúng ở nhiệt độ t₁ = 10⁰C. Nếu nhiệt độ tăng đến 20⁰C thì mỗi ngày đêm đồng hồ nhanh hay chậm bao nhiêu? Cho hệ số nở dài của dây treo con lắc là α = 2.10^-5K^-1.

A. Nhanh 17,28s.

B. Chậm 8,64s.

C. Chậm 17,28s.

D. Nhanh 8,64s

Xem đáp án

Chọn B

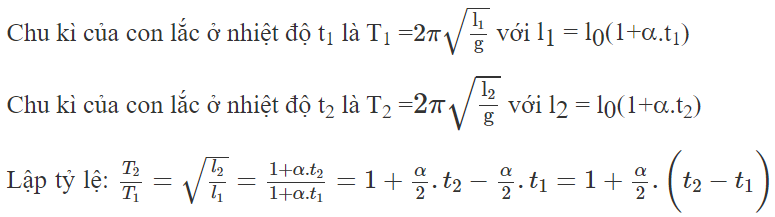
(phép biến đổi có sử dụng công thức gần đúng)

+ Mỗi chu kỳ đồng hồ chỉ sai thời gian ΔT.

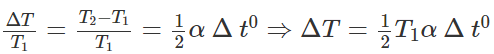
+ Do ΔT > 0 đồng hồ chạy chậm và mỗi ngày chậm:

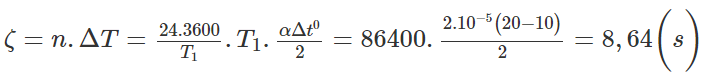
Câu 22:

Một đồng hồ quả lắc chạy đúng giờ trên mặt đất. Biết bán kính Trái Đất là 6400km và coi nhiệt độ không ảnh hưởng đến chu kì của con lắc. Đưa đồng hồ lên đỉnh núi cao 640m so với mặt đất thì mỗi ngày đồng hồ chạy nhanh hay chậm bao nhiêu?

A. nhanh 8,64s.

B. nhanh 17,28s.

C. chậm 17,28s.

D. chậm 8,64s.

Xem đáp án

Chọn D

Chu kì của con lắc ở mặt đất là:

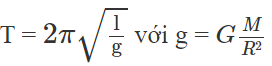
Chu kì của con lắc ở độ cao h là T’:

Lập tỷ lệ:

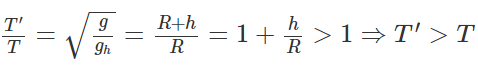
Þ Đồng hồ chạy chậm hơn so với ở mặt đất

Mỗi chu kì đồng hồ sai thời gian ΔT:

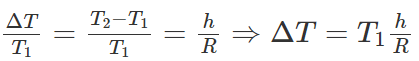
Do ΔT > 0 đồng hồ chạy chậm và mỗi ngày chậm:

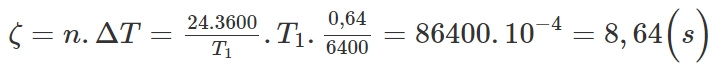
Câu 23:

Một đồng hồ quả lắc chạy đúng giờ trên mặt đất. Đưa đồng hồ xuống giếng sâu d = 400m so với mặt đất. Coi nhiệt độ không đổi. Bán kính Trái Đất R = 6400km. Sau một tuần lễ đồng hồ đó chạy nhanh hay chậm bao nhiêu?

A. nhanh 2,7s

B. nhanh 18,9s

C. chậm 2,7s

D. chậm 18,9s.

Xem đáp án

Chọn D

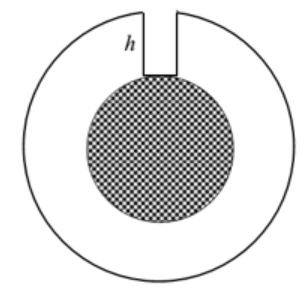
- Khối lượng trái đất là:

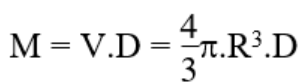với R là bán kính trái đất

- Khối lượng phần trái đất tính từ độ sâu h đến tâm là:

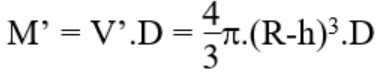
- Gia tốc trọng trường trên mặt đất là: $g = G \frac{M}{R^{2}}$

- Gia tốc trọng trường ở độ sâu h là: $g' = G \frac{M'}{{(R - h)}^{2}}$

- Gọi T là chu kì của con lắc trên mặt đất là: $T = 2 π \sqrt{\frac{l}{g}}$

- Gọi T’ là chu kì của con lắc ở độ sâu h là T’: $T' = 2 π \sqrt{\frac{l}{g'}}$

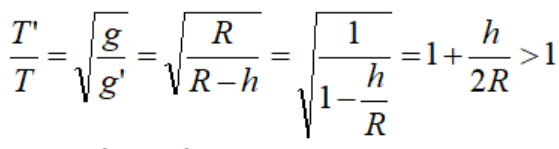
$\Rightarrow$ T'>T $\Rightarrow$ Đồng hồ chạy chậm hơn

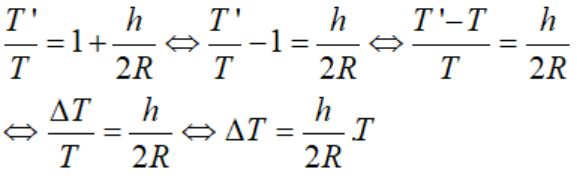
+ Do ΔT > 0 đồng hồ chạy chậm và một tuần lễ chậm:

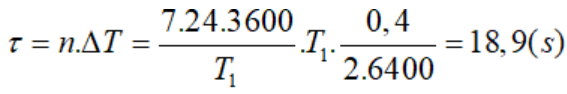
Câu 24:

Một đồng hồ quả lắc chạy đúng giờ tại Hà Nội với chu kỳ T = 2s. Đưa con lắc vào Hồ Chí Minh giả sử nhiệt độ không thay đổi. Tại Hồ Chí Minh con lắc chạy nhanh hay chậm? Sau 12giờ nó chạy nhanh hay chậm bao nhiêu thời gian? Biết gia tốc ở Hà Nội và Hồ Chí Minh lần lượt là: g₁ = 9,793m/s² và g₂= 9,787m/s².

A. nhanh 1,323s.

B. chậm 1,323 s

C. chậm13,23 s.

D. nhanh 13,23 s.

Xem đáp án

Chọn C

+ Mỗi chu kỳ đồng hồ chỉ sai thời gian ΔT:

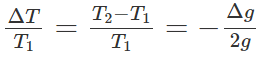
+ Do $∆ g = g_{2} - g_{1}$ =9,787-9,793=-0,006<0 nên ΔT >0 đồng hồ chạy chậm.

+ Mỗi chu kỳ đồng hồ chỉ sai thời gian ΔT nên 12 giờ đồng hồ chậm:

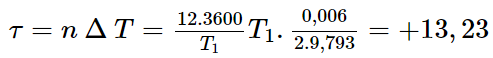
Câu 25:

Một vật có khối lượng 100g dao động điều hòa. Khi hợp lực tác dụng lên vật có độ lớn 0,8N thì nó đạt tốc độ 0,6m/s. Khi hợp lực tác dụng lên vật có độ lớn $\frac{\sqrt{2}}{2}$ N thì nó đạt tốc độ $\frac{\sqrt{2}}{2}$ m/s. Cơ năng của vật là:

A. 2,5J.

B. 0,05J.

C. 0,25J.

D. 0,5J.

Xem đáp án

Chọn B

+ Ta có vận tốc và hợp lực tác dụng lên vật vuông pha với nhau nên

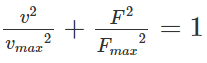
$\Rightarrow$ hệ phương trình: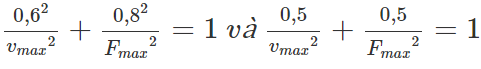

=> v_max = 1m/s; F_max = 1N.

+ Lại có:

Một vật có khối lượng 100g dao động điều hòa. Khi hợp lực tác (ảnh 3)

CHỌN BỘ SÁCH BẠN MUỐN XEM

150 câu trắc nghiệm Dao động cơ cơ bản

150 câu trắc nghiệm Dao động cơ cơ bản (Phần 3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương