5 câu hỏi trắc nghiệm thuộc Đề thi Vật lý ôn vào 10 hệ chuyên có đáp án (Mới nhất) (Đề 13)

Câu 1:

Trên dòng sông, nước chảy với vận tốc u, có hai tàu thủy đi lại gặp nhau. Tại một thời điểm nào đó, khi một tàu thủy qua địa điểm A thì chiếc tàu thủy kia đi qua địa điểm B, đồng thời từ A có một xuồng máy chạy qua chạy lại giữa hai tàu thủy nói trên cho tới khi hai tàu thủy gặp nhau. Khoảng cách giữa hai địa điểm A và B theo bờ sông là L. Vận tốc của tàu thủy và của xuồng máy khi nước yên lặng là v và V. Địa điểm A nằm ở thượng nguồn.

a. Xác định thời gian xuồng máy đã chuyển động từ địa điểm A cho đến khi hai tàu thủy gặp nhau.

b. Xác định quãng đường mà xuồng máy đã chạy trong thời gian nói trên. Câu trả lời như thế nào nếu xuồng máy xuất phát từ B

Xem đáp án

a.Vận tốc của tàu A là v_A = v + u, của tàu B là: v_B = v – u

Thời gian để hai tàu gặp nhau là:

$t = \frac{L}{v + u + v - u} = \frac{L}{2 v}$ , đó cũng là thời gian xuồng máy chuyển động.

b.

Vận tốc xuồng máy khi xuôi dòng là: $V_{x} = V + u$

Vận tốc xuồng máy khi ngược dòng là: $V_{n} = V - u$

Trên dòng sông, nước chảy với vận tốc u, có hai tàu thủy đi lại gặp nhau. Tại một thời điểm nào đó, khi một tàu thủy qua địa điểm (ảnh 1)

Theo sơ đồ trên ta có: AB₁ = A₁B₁+ AA₁

A₁B₂ = A₂B₂+ A₁A₂

..............

=> (AB_{1 +} A₁B₂+............) = (A₁B₁+ A₂B₂+ .......) + (AA₁+ A₁A₂+.......)

V ới

AB_{1 +} A₁B₂+................: là tổng quãng đường s_x xuồng máy đi xuôi dòng.

A₁B₁+ A₂B₂+ ............: là tổng quãng đường s_n xuồng máy đi xuôi dòng.

Có s_x = s_n + s_A (1) trong đó $s_{A} = t . v_{A} = \frac{L}{2 v} . (v + u)$ (2)

Gọi t_x là tổng thời gian xuồng máy đi xuôi dòng, t_n là tổng thời gian xuồng máy đi ngược dòng thì: t = t_x+ t_n

_{$\Rightarrow \frac{s_{x}}{V + u} + \frac{s_{n}}{V - u} = \frac{L}{2 v}$}

Thay (1) ; (2) vào (3) thì:

$\frac{s_{n}}{V + u} + \frac{s_{n}}{V - u} + \frac{L}{2 v} . \frac{v + u}{V + u} = \frac{L}{2 v} \Rightarrow \frac{s_{n} .2 V}{V^{2} - u^{2}} = \frac{L}{2 v} . (1 - \frac{v + u}{V + u}) \Rightarrow \frac{s_{n} .2 V}{V^{2} - u^{2}} = \frac{L}{2 v} . \frac{V - v}{V + u} \begin{array}{l} \Rightarrow s_{n} = \frac{L}{2 v} . \frac{V - v}{V + u} . \frac{V^{2} - u^{2}}{2 V} = \frac{L}{4 V v} . (V - v) . (V - u) \\ \Rightarrow s_{x} + s_{n} = 2 s_{n} + s_{A} = \frac{L}{2 V v} . (V - v) . (V - u) + \frac{L}{2 v} . (u + v) \end{array} \Rightarrow s_{x} + s_{n} = \frac{L}{2 V v} . (V^{2} + u v)$

Trường hợp xuồng máy xuất phát từ B thì ta thay u bởi - u trong công thức (4) tổng quãng đường là: $\frac{L}{2 V v} . (V^{2} - u v)$

Câu 2:

Một bình hình trụ có bán kính đáy là R₁ = 20cm chứa nước ở nhiệt độ t₁ = 20⁰C đặt trên mặt bàn nằm ngang. Người ta thả một quả cầu đặc bằng nhôm có bán kính R₂ = 10cm ở nhiệt độ t₂ = 40⁰C vào bình thì mực nước ngập chính giữa quả cầu. Bỏ qua sự trao đổi nhiệt giữa nước, quả cầu với bình và môi trường; cho biết khối lượng riêng của nước là D₁= 1000 kg/m³ và của nhôm là D₂ = 2700 kg/m³; nhiệt dung riêng của nước là c₁ = 4200 J/kg.K và của nhôm là c₂ = 880 J/kg.K.

a. Tìm nhiệt độ của nước khi có cân bằng nhiệt.

b. Đổ thêm dầu ở nhiệt độ t₃ = 15⁰C vào bình cho vừa đủ ngập quả cầu. Biết khối lượng riêng của dầu là D₃= 800 kg/m³, nhiệt dung riêng của dầu là c₃ = 2800 J/kg.K. Bỏ qua sự trao đổi nhiệt giữa nước, dầu, quả cầu với bình và môi trường. Hãy xác định nhiệt độ của hệ khi cân bằng nhiệt, áp lực của quả cầu lên đáy bình. Cho biết công thức tính thể tích hình cầu là $V_{c} = \frac{4}{3} π {R_{c}}^{3}$ , thể tích hình trụ là $V_{t r} = π {R_{t r}}^{2} h$ , lấy $π = 3, 14$ .

Xem đáp án

a.

Tìm nhiệt độ của nước khi cân bằng

Thể tích chất lỏng trong bình $V_{1} = π R_{1}^{2} R_{2} - \frac{1}{2} . \frac{4}{3} π R_{2}^{3}$

Khối lượng của bình là : $m_{1} = V_{1} D_{1} = (π R_{1}^{2} R_{2} - \frac{1}{2} . \frac{4}{3} π R_{2}^{3}) D_{1}$

Thay số ta được m₁ = 10,47kg

Khối lượng của quả cầu : $m_{2} = D_{2} V_{2} = \frac{4}{3} π R_{2}^{3} D_{2} = 11, 3 k g$

Từ điều kiện của bài toán cho, ta có phương trình cân bằng nhiệt

m_{1} c_{1} (t - t_{1}) = m_{2} c_{2} (t - t_{2})

với t là nhiệt đôi hỗn hợp khi cân bằng

Do đó, ta có nhiệt độ khi cân bằng là

t = \frac{m_{1} c_{1} t_{1} + m_{2} c_{2} t_{2}}{m_{1} c_{1} + m_{2} c_{2}}

thay số t ≈ 23,7⁰c

b.

Do thể tích của dầu và nước bằng nhau nên khối lượng của dầu là

$\frac{m_{3}}{D_{3}} = \frac{m_{1}}{D_{1}} \Rightarrow m_{3} = \frac{m_{1} D_{3}}{D_{1}}$ thay số ta được m₃ ≈ 8,38kg

Khi cân bằng nhiệt ta được nhiệt độ của hệ là t_x.

Phương trình cân bằng nhiệt

$m_{1} c_{1} (t - t_{x}) + m_{2} c_{2} (t - t_{x}) = m_{3} c_{3} (t_{x} - t_{3})$ → $t_{x} = \frac{m_{1} c_{1} t + m_{2} c_{2} t + m_{3} c_{3} t_{3}}{m_{1} c_{1} + m_{2} c_{2} + m_{3} c_{3}}$

Thay số t_x ≈ 21,06⁰c

Áp lực của quả cầu lên đáy bình : $F = P - F_{A} = 10 m_{2} - \frac{1}{2} . \frac{4}{3} π R_{2}^{3} (D_{1} + D_{3}) .10$

Thay số: F ≈ 75N

Câu 3:

Cho mạch điện (như hình 1). Đặt vào hai đầu của đoạn mạch một hiệu điện thế U_AB = 18V. Biến trở R_b có điện trở toàn phần R_MN = 20 $Ω$ , R₁ = 2 $Ω$ ; đèn có điện trở = 2; vôn kế có điện trở rất lớn và ampe kế có điện trở nhỏ không đáng kể.

1. Điều chỉnh con chạy C để ampe kế chỉ 1A.

a. Xác định vị trí con chạy C.

b. Tìm số chỉ vôn kế khi đó.

c. Biết đèn sáng bình thường. Tìm công suất định mức của đèn.

2. Phải di chuyển con chạy C đến vị trí nào để công suất tiêu thụ trên biến trở đạt giá trị lớn nhất? Giá trị lớn nhất ấy bằng bao nhiêu? Cho biết độ sáng của đèn lúc này.

3. Biết đèn chịu được hiệu điện thế tối đa là 4,8V. Hỏi con chạy C chỉ được dịch chuyển trong khoảng nào của biến trở để đèn không bị cháy?

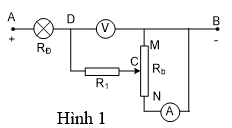
Cho mạch điện (như hình 1). Đặt vào hai đầu của đoạn mạch một hiệu điện thế UAB = 18V. Biến trở Rb có điện trở toàn phần RMN = 20 , R1 (ảnh 1)

Xem đáp án

a.

+ Mạch gồm : (R_CM//R_CN )ntR₁ntRđ

Đặt R_CM = x thì R_CN = 20 -x với ; $0 \leq x \leq 20 Ω$ $R_{C B} = \frac{x (20 - x)}{20}$

+ $R_{A B} = R {}_{1}+ R_{d} + R_{C B} = 4 + \frac{x (20 - x)}{20} = \frac{- x^{2} + 20 x + 80}{20}$

+ $I_{A B} = \frac{U_{A B}}{R_{A B}} = \frac{18.20}{- x^{2} + 20 x + 80}$

+ $I_{A} = \frac{U_{C B}}{R_{C N}} = \frac{18 x (20 - x)}{- x^{2} + 20 x + 80} \cdot \frac{1}{20 - x} = \frac{18 x}{- x^{2} + 20 x + 80}$

+ Ampe kế chỉ 1A $\Rightarrow \frac{18 x}{- x^{2} + 20 x + 80} = 1 \Rightarrow x^{2} - 2 x - 80 = 0$

+ Giải phương trình ta được x = 10W hoặc x = -8 (loại)

+ Vậy con chạy C ở chính giữa biến trở thì ampe kế chỉ 1A

b.

Với x = 10W ta có

+ ; $I_{A B} = \frac{18.20}{- 10^{2} + 20.10 + 80} = 2 (A); U_{Ð} = I_{A B} R_{Ð} = 2.2 = 4 (V)$

+ Số chỉ của vôn kế là:

U_{V} = U_{A B} - U_{Ð} = 18 - 4 = 14 (V)

c.

+ Công suất định mức của đèn là:

P_{Ð (đ m)} = P_{Ð} = \frac{U_{Ð}^{2}}{R_{Ð}} = \frac{4^{2}}{2} = 8 (W)

2.

Đặt ; $y = R_{CB} = \frac{x (20 - x)}{20}; R_{A B} = R_{Ð} + R_{1} + R_{C B} = 4 + y I_{A B} = \frac{U_{A B}}{R_{A B}} = \frac{18}{y + 4}$

Công suất tiêu thụ trên biến trở là:

+ $P_{C B} = I_{A B}^{2} R_{C B} = {(\frac{18}{y + 4})}^{2} . y = {(\frac{18}{\sqrt{y} + \frac{4}{\sqrt{y}}})}^{2}$

+ Áp dụng BĐT côsi ta có: $\sqrt{y} + \frac{4}{\sqrt{y}} \geq 2 \sqrt{4} = 4$

+ $\Rightarrow P_{C B} \leq {(\frac{18}{4})}^{2} = 20, 25$

+ Dấu "=" xảy ra khi $\sqrt{y} = \frac{4}{\sqrt{y}} \Rightarrow y = 4 \Rightarrow \frac{- x^{2} + 20 x}{20} = 4 \Rightarrow [\begin{array}{l} x \approx 14, 5 \\ x \approx 5, 5 \end{array}$

+ Vậy con chạy C ở vị trí sao cho $R_{C M} = 5, 5 Ω$ hoặc $R_{C M} = 14, 5 Ω$ thì công suất tiêu thụ trên biến trở đạt cực đại, giá trị cực đại bằng 20,25W.

Cường độ dòng điện trong mạch lúc đó là:

+ $I_{A B} = \frac{18}{y + 4} = \frac{18}{4 + 4} = 2, 25 (A)$ $\Rightarrow U_{Ð} = I_{A B} R_{Ð} = 2, 25.2 = 4, 5 (V)$

+ Đèn sáng hơn bình thưng

3.

+ $U_{Ð} = I_{A B} R_{Ð} = \frac{18}{y + 4} \cdot 2 = \frac{36}{y + 4}$

+ $U_{Ð} \leq 4, 8 (V) \Rightarrow \frac{36}{y + 4} \leq 4, 8 \Rightarrow y \geq 3, 5$ $\Rightarrow \frac{- x^{2} + 20 x}{20} \geq 3, 5$

+ $\Rightarrow - x^{2} + 20 x - 70 \geq 0 = > \Rightarrow 4, 5 \leq x \leq 15, 5$

+ Vậy con chạy C chỉ được di chuyển trong khoảng sao cho điện trở của đoạn CM có giá trị từ 4,5W đến 15,5W

Câu 4:

Một thấu kính hội tụ tiêu cự f .

1. Một điểm sáng S qua thấu kính cho ảnh thật S^’. Gọi khoảng cách từ S đến thấu kính là d; từ S’ đến thấu kính là d’. Chứng minh công thức $\frac{1}{d} + \frac{1}{d'} = \frac{1}{f}$ .

2. Điểm sáng A đặt trên trục chính của thấu kính hội tụ cách thấu kính một khoảng OA = 60cm. Tiêu cự của thấu kính f = 40cm. Cho điểm sáng A chuyển động trong thời gian 16 giây với vận tốc 0,5cm/s theo phương hợp với trục chính một góc α = 60⁰ lại gần về phía thấu kính. Xác định vận tốc trung bình của ảnh và góc β hợp bởi phương chuyển động của ảnh với trục chính.

Xem đáp án

Vẽ đúng hình

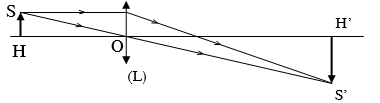
Một thấu kính hội tụ tiêu cự f . 1. Một điểm sáng S qua thấu kính cho ảnh thật S’. Gọi khoảng cách từ S đến thấu kính là d; từ S’ đến thấu kính là d’. Chứng minh công thức . 2. Điểm sáng A đặt trên trục chính (ảnh 1)

Ảnh ngược chiều với vật đó là ảnh thật

Dùng tam giác đồng dạng chứng minh được công thức:

\frac{1}{f} = \frac{1}{d} + \frac{1}{d^{/}}

b.

Khi điểm sáng từ A đến B với AB = v.t = 8cm thì ảnh đi từ A’ đến B’

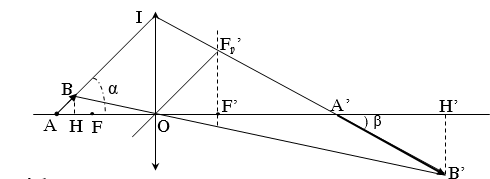
Nêu cách vẽ ảnh A’B’

Tính chiều dài của ảnh

Dựng BH và B’H’ vuông góc với trục chính

Do OA = d = 60cm, mà $\frac{1}{f} = \frac{1}{d} + \frac{1}{d^{/}}; O A^{'} = d' = \frac{d f}{d - f} = \frac{60.40}{60 - 40} = 120 c m$ \

Tacó $A H = \cos 60^{0} . A B = 4 c m \Rightarrow O H = O A - A H = 56 c m$

$\frac{1}{f} = \frac{1}{O H} + \frac{1}{O H'} \Rightarrow O H' = \frac{O H . f}{O H - f} = \frac{56.40}{56 - 40} = 140 c m$

Mà A’H’= OH’- OA’=140 -120 =20cm $\{\begin{cases} \tan β = \frac{O I}{O A'} \\ \tan α = \frac{O I}{O A} \end{cases} \Rightarrow \frac{\tan β}{\tan α} = \frac{O A}{O A'} \Rightarrow \tan β = \tan α . \frac{O A}{O A'} = \sqrt{3} . \frac{60}{120} = \frac{\sqrt{3}}{2}$

Suy ra góc hợp bởi quỹ đạo và trục chính là β 40,9⁰

Ta có $H' B' = \tan β . A' H' = \frac{\sqrt{3}}{2} .20 = 10 \sqrt{3} c m$

Theo định lí pitago ta có

$A' B' = \sqrt{{(A' H')}^{2} + {(H' B')}^{2}} = \sqrt{20^{2} + {(10 \sqrt{3})}^{2}} = 10 \sqrt{7} c m$

Vận tốc trung bình của ảnh:

v' = \frac{A' B'}{t} = \frac{10 \sqrt{7}}{16} = \frac{5 \sqrt{7}}{8} \approx

1,65cm/s

Câu 5:

Cho các dụng cụ:

- Một vật có khối lượng m =10 gam.

- Một thước kẻ học sinh có độ chia nhỏ nhất là 1mm và giới hạn đo là 20cm.

- Một giá đỡ.

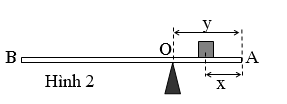
Cho các dụng cụ: - Một vật có khối lượng m =10 gam. - Một thước kẻ học sinh có (ảnh 1)

Để xác định chiều dài L và khối lượng M của một thanh đồng chất, tiết diện đều (chiều dài của thanh lớn hơn chiều dài của thước), một học sinh sử dụng các dụng cụ trên và đã tiến hành một thí nghiệm như sau:

Đặt vật khối lượng m lên trên thanh ở cách đầu A của thanh một đoạn là x, thanh nằm cân bằng trên một điểm tựa tại O trên giá đỡ cách đầu A một đoạn là y (như hình 2). Khi vật m đặt ở các vị trí khác nhau, để đảm bảo cho thanh cân bằng theo phương nằm ngang, học sinh đó thu được bảng số liệu như sau:

x (mm)	10	30	50	70	90	100	120
y (mm)	120	129	137	146	155	160	162

a. Thiết lập mối quan hệ giữa y với x, M, m và L trong trường hợp thanh cân bằng theo phương nằm ngang.

b. Từ bảng số liệu thu được ở trên, em hãy vẽ đồ thị biểu diễn sự phụ thuộc của y theo x. Từ đó xác định khối lượng M và chiều dài L của thanh.

Xem đáp án

a.

Thanh đồng chất tiết diện đều nên trọng tâm nằm ở giữa thanh

Điều kiện cân bằng của thanh

10M.(l₀ – y) = 10m.(y - x) Với L = 2l₀

$\frac{l_{0} - y}{y - x} = \frac{m}{M} = a \Rightarrow \frac{l_{0} - y}{y - x} = a \Rightarrow y = \frac{a}{a + 1} x + \frac{l_{0}}{a + 1}$

Sự phụ thuộc của y theo x tuân theo một hàm số bậc nhất

b.

Từ số liệu thu được

vẽ được đồ thị hình bên

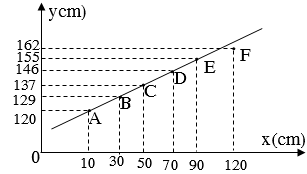
Cho các dụng cụ: - Một vật có khối lượng m =10 gam. - Một thước kẻ học sinh có (ảnh 2)

Ta thấy các điểm A,C,D,E nằm phân bố trên một đường thẳng nên coi các giá trị đó tương đối chính xác còn điểm F (x=120, y=162) nằm xa đường thẳng sai số lớn nên bỏ qua

Như trên $\frac{l_{0} - y}{y - x} = a$ không đổi. Vậy ta có

$\frac{l_{0} - 120}{120 - 10} = \frac{l_{0} - 137}{137 - 50} \to l_{0} = 201, 3 m m$ suy ra L = 2l₀ = 402,6mm

Tương tự

$\frac{l_{0} - 137}{137 - 50} = \frac{l_{0} - 146}{146 - 70} \to l_{0} = 208, 2 m m$ suy ra L = 2l₀ = 416,4mm

$\frac{l_{0} - 146}{146 - 70} = \frac{l_{0} - 155}{155 - 90} \to l_{0} = 208, 2 m m$ suy ra L = 2l₀ = 416,4mm

Chiều dài của thanh là

$L = \frac{402, 6 + 416, 4 + 416, 4}{3} = 411, 8 m m \approx 412 m m$ ; l₀ = 206 mm

Với điểm A: $\frac{206 - 120}{120 - 10} = \frac{10}{M} \to M = 12, 8 g$

Với điểm C: $\frac{206 - 137}{137 - 50} = \frac{10}{M} \to M = 12, 6 g$

Với điểm D: $\frac{206 - 146}{146 - 70} = \frac{10}{M} \to M = 12, 7 g$

Khối lượng của thanh là

M = \frac{12, 8 + 12, 6 + 12, 7}{3} = 12, 7 g

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất)

Đề thi Vật lý ôn vào 10 hệ chuyên có đáp án (Mới nhất) (Đề 13)

Danh sách câu hỏi

Bài thi liên quan