5 câu hỏi trắc nghiệm thuộc Đề thi Vật lý ôn vào 10 hệ chuyên có đáp án (Mới nhất) (Đề 11)

Câu 1:

Ba chất lỏng khác nhau có khối lượng m₁, m₂, m₃; nhiệt dung riêng và nhiệt độ đầu tương ứng là c₁, c₂, c₃ và t₁ = 90⁰C, t₂ = 20⁰C, t₃ = 60⁰C có thể hòa lẫn vào nhau và không có tác dụng hóa học. Nếu trộn chất lỏng thứ nhất với nửa chất lỏng thứ ba thì nhiệt độ cân bằng của hỗn hợp là t₁₃ = 70⁰C, nếu trộn chất lỏng thứ hai với nửa chất lỏng thứ ba thì nhiệt độ cân bằng của hỗn hợp là t₂₃ = 30⁰C. Cho rằng chỉ có sự trao đổi nhiệt giữa các chất lỏng với nhau.

a. Viết phương trình cân bằng nhiệt của mỗi lần trộn.

b. Tính nhiệt độ cân bằng t_c khi trộn cả ba chất lỏng với nhau

Xem đáp án

a. Phương trình cân bằng nhiệt:

- Lần 1: m₁c₁(t₁ – t₁₃) = 1/2m₃c₃(t₁₃ – t₃) => m₁c₁(90 – 70) = 1/2m₃c₃(70 – 60)

<=> 20m₁c₁ = 5m₃c₃ => 4m₁c₁ = m₃c₃

- Lần 2: m₂c₂(t₂₃ – t₂) = 1/2m₃c₃(t₃ - t₂₃) => m₂c₂ (30 – 20) = 1/2m₃c₃(60 – 30)

<=>10m₂c₂ =15m₃c₃ => m₂c₂ = 1,5m₃c₃

_b.

Tính t_c

- Ta có: m₁c₁ = 0,25m₃c₃ (1)

m₂c₂ = 1,5m₃c₃ (2)

- Gọi t_c là nhiệt độ chung khi trộn ba chất lỏng với nhau; nhiệt lượng mỗi chất lỏng thu vào hoặc tỏa ra trong khi trao đổi nhiệt là:

Q₁ = m₁c₁(t₁ – t_c), Q₂ = m₂c₂(t₂ – t_c), Q₃ = m₃c₃(t₃ – t_c)

- Theo định luật bảo toàn nhiệt lượng thì: Q₁ + Q₂ + Q₃ = 0

=> m₁c₁(t₁ – t_c) + m₂c₂(t₂ – t_c) + m₃c₃(t₃ – t_c) = 0 (3)

- Từ (1), (2), (3) giải ra ta được t_c = 40,9⁰C

Câu 2:

Tại hai địa điểm A và B trên một đường thẳng, lúc 6 giờ có hai xe chuyển động, một xe xuất phát tại A và một xe xuất phát tại B theo hướng AB với vận tốc không đổi. Nếu xuất phát cùng lúc thì hai xe gặp nhau tại điểm C sau 3 giờ chuyển động, nếu xe tại A xuất phát chậm 10 phút thì hai xe gặp nhau tại D. Biết AB = 30km, CD = 20km. Hãy xác định:

a. Vận tốc của mỗi xe.

b. Thời điểm hai xe gặp nhau tại C và D.

Xem đáp án

a. Gọi v₁ là vận tốc xe đi từ A, v₂ là vận tốc xe đi từ B.

- Chuyển động lần 1: v₁t - v₂t = 30

=> v₁ - v₂ = 30/t = 10 (1)

- Chuyển động lần 2:

v₁t₁ = v₁t + 20 => t₁ = (v₁t + 20)/v₁

t₁ = (3v₁ + 20)/v₁ (2)

(v₂t₁ + v₂/6) - v₂t = 20

=> t₁ = (20 - v₂/6 + 3v₂)/v₂

Từ 1, 2, 3 có phương trình: v₂² + 10v₂ - 1200 = 0;

- Giải phương trình tính được v₂ = 30km/h => v₁ = 40km/h.

Vận tốc của xe tại A là v₁ = 40km/h; của xe tại B là v₂ = 30km/h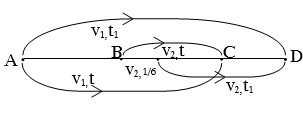

Tại hai địa điểm A và B trên một đường thẳng, lúc 6 giờ có hai xe chuyển động, một xe xuất phát tại A và một xe xuất phát tại (ảnh 1)

b.

- Gặp nhau lần đầu tại C lúc: 6 giờ + 3 giờ = 9 giờ 00

- Thời gian gặp lần sau: t₁ = (3.40 + 20)/40 = 3 giờ 30 phút

- Lúc đó là: 6 giờ + 3 giờ 30 phút + 10 phút = 9 giờ 40 phút

Câu 3:

Cho mạch điện như hình vẽ H1. Biết U không đổi, R₄là biến trở, R₁, R₂, R₃là các điện trở cho sẵn. Bỏ qua điện trở của ampe kế và các dây nối.

a. Chứng tỏ rằng khi điều chỉnh R₄ để ampe kế chỉ số 0 thì $\frac{R_{1}}{R_{2}} = \frac{R_{3}}{R_{4}}$ .

b. Cho R₁ = 4, R₂ = 3, R₃ = 12, U = 6V. Xác định giá trị của R₄ để dòng điện qua ampe kế theo chiều từ C đến D là 0,1A.

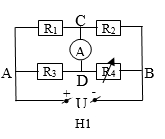
Cho mạch điện như hình vẽ H1. Biết U không đổi, R4 là biến trở (ảnh 1)

Xem đáp án

I_A = 0 và U_CD = 0

Mạch gồm (R₁//R₃)nt(R₂//R₄)=> U₁ = U₃; U₂ = U₄. (1)

Hoặc (R₁ntR₂)//(R₃ntR₄) => I₁ = I₂; I₃ = I₄.

- => U₁/R₁ = U₂/R₂; U₃/R₃ = U₄/R₄ (2)

- Từ (1) và (2) =>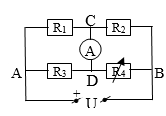

\frac{R_{1}}{R_{2}} = \frac{R_{3}}{R_{4}}

- Mạch gồm (R₁//R₃)nt(R₂//R₄)

- Ta có : I₁R₁ + (I₁ – I_A)R₂ = U ó 4I₁ + (I₁ – 0,1)3 = 6

=> I₁ = 0,9A

- U₁ = U₃ = I₁R₁ = 0,9.4 = 3,6V => U₂ = U₄ = U – U₁ = 2,4V.

- I₃ = U₃/R₃ = 3,6/12 = 0,3A ; I₄ = I₃ + I_A = 0,3 + 0,1 = 0,4A

- R₄ = U₄/I₄ = 2,4/0,4 = 6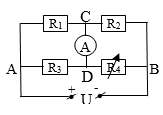

Cho mạch điện như hình vẽ H1. Biết U không đổi, R4 là biến trở (ảnh 2)

Câu 4:

Cho mạch điện như hình vẽ H2. Biết U không đổi, R₁ = R₂ = R₃ = r, đèn Đ có điện trở R_đ = kr, R_b là biến trở. Bỏ qua điện trở của các dây nối.

a. Điều chỉnh R_b để đèn tiêu thụ công suất bằng 4W. Tính công suất tiêu thụ trên R₂ theo k.

b. Cho U = 12V, r = 6, k = 2, R_b = 3. Tính công suất tiêu thụ trên đèn Đ.

Xem đáp án

a.

Ta có I₁ + I_đ = I₂ + I₃ => U₁/r + U_đ/kr = U₂/r + U₃/r

=> U₁ + U_đ/k = U₂ + U₃ ó U₁ + U_đ/k = U₂ + (U₁ + U₂) – U_đ

=> $U_{2} = \frac{U_{đ}}{2} (\frac{k + 1}{k})$

- P_đ $= \frac{U_{đ}^{2}}{kr}$ ó $4 = \frac{U_{đ}^{2}}{kr} \Rightarrow U_{đ}^{2} = 4kr$

- P_R2 =

\frac{U_{2}^{2}}{R_{2}}

=

\frac{\frac{U_{đ}^{2}}{4} \frac{{(k + 1)}^{2}}{k^{2}}}{r}

=

\frac{\frac{4kr}{4} \frac{{(k + 1)}^{2}}{k^{2}}}{r} = \frac{{(k + 1)}^{2}}{k}

b. Chọn chiều dòng điện như hình vẽ:

- Ta có: I₁R₁ + (I₁ – I_b)R₂ = U ó 6I₁ + 6(I₁ – I_b) = 12 => I₁ = 1 + 0,5I_b (1)

I₁R₁ + I_bR_b + (I_đ + I_b)R₃ = U => 6I₁ + 3I_b + (I_b + I_đ)6 = 12

=> I₁ + 0,5I_b + I_b + I_đ = 2 => I₁ + 1,5I_b + I_đ = 2 (2)

I_đR_đ + (I_b + I_đ)R₃ = U => 12I_đ + (I_b + I_đ)6 = 12

=> 2I_đ + I_b + I_đ = 2 => 3I_đ + I_b = 2 (3)

Từ (1) và (2) => 2I_b + I_đ = 1 (4)

Giải (3) và (4) tính được I_đ = 0,6A; I_b = 0,2A

- P_Đ = I_đ²R_đ = 0,6².12 = 4,32W

Câu 5:

Đặt vật sáng AB = 2cm vuông góc với trục chính $Δ$ của một thấu kính hội tụ có quang tâm O, tiêu điểm F; A nằm trên trục chính. Qua thấu kính vật AB cho ảnh A’B’ cùng chiều và cao gấp 5 lần vật.

a. Vẽ ảnh A’B’ của AB qua thấu kính. Dựa vào hình vẽ chứng minh công thức sau: $\frac{1}{O F} = \frac{1}{O A} - \frac{1}{O A'}$ . Khi AB dịch chuyển dọc theo trục chính lại gần thấu kính thì ảnh của nó dịch chuyển theo chiều nào ? Giải thích ?

b. Bây giờ đặt vật AB nằm dọc theo trục chính của thấu kính, đầu A vẫn nằm ở vị trí cũ, đầu B hướng thẳng về quang tâm O. Nhìn qua thấu kính thì thấy ảnh của AB cũng nằm dọc theo trục chính và có chiều dài bằng 30cm. Hãy tính tiêu cự của thấu kính.

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất)

Đề thi Vật lý ôn vào 10 hệ chuyên có đáp án (Mới nhất) (Đề 11)

Danh sách câu hỏi

Bài thi liên quan