Đề thi Giữa kì 1 Vật lí 12 có đáp án (Đề 6)
-
1412 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong đoạn mạch xoay chiều RLC nối tiếp, dòng điện và hiệu điện thế cùng pha khi
 Xem đáp án
Xem đáp án
Trong đoạn mạch xoay chiều RLC nối tiếp, dòng điện và hiệu điện thế cùng pha khi trong đoạn mạch xảy ra hiện tượng cộng hưởng điện.
Chọn đáp án C
Câu 2:
 Xem đáp án
Xem đáp án
Trong dao động tắt dần thì cơ năng và biên độ giảm dần theo thời gian.
Chọn đáp án B
Câu 3:
 Xem đáp án
Xem đáp án
+ Chu kì dao động mạch LC: \(T = 2\pi \sqrt {LC} = 0,02\left( s \right)\)
+ Tại thời điểm t = 0: \(q = {Q_0}\)
+ Thời gian ngắn nhất từ lúc điện tích trên tụ điện có giá trị bằng một nửa giá trị ban đầu: \({t_{\min }} = \frac{T}{6} = \frac{1}{{300}}\left( s \right)\)
Chọn đáp án C
Câu 4:
 Xem đáp án
Xem đáp án
Độ lớn vận tốc khi đi qua vị trí có li độ x: \[v = \omega \sqrt {{A^2} - {x^2}} \]
Chọn đáp án B
Câu 5:
 Xem đáp án
Xem đáp án
\(i = q' = {3.10^{ - 6}}.2000.\cos \left( {2000t + \frac{\pi }{2}} \right) = {6.10^{ - 3}}\cos \left( {2000t + \frac{\pi }{2}} \right)\left( A \right)\)
Chọn đáp án B
Câu 6:
 Xem đáp án
Xem đáp án
Ta có: \({u_L}\)ngược pha \({u_C}\)
\(\Rightarrow \frac{{{u_C}}}{{{u_L}}} = - \frac{{{Z_C}}}{{{Z_L}}} \Rightarrow {u_C} = - \frac{{{Z_C}}}{{{Z_L}}}{u_L}\)
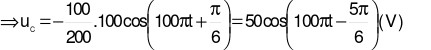
Chọn đáp án A
Câu 7:
 Xem đáp án
Xem đáp án
Chu kì dao động riêng của mạch:
\(T = 2\pi \sqrt {LC} = {2.10^{ - 6}}\left( s \right)\)
Chọn đáp án D
Câu 8:
 Xem đáp án
Xem đáp án
Mạch dao động LC dao động điều hòa với tần số f, khi đó \(f = \frac{1}{{2\pi \sqrt {LC} }}\)
Chọn đáp án C
Câu 9:
 Xem đáp án
Xem đáp án
Điện trường xoáy là điện trường có các đường sức bao quanh các đường sức từ.
Chọn đáp án D
Câu 10:
 Xem đáp án
Xem đáp án
Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là 0,3s
\( \Rightarrow \frac{T}{4} = 0,3 \Rightarrow T = 1,2\left( s \right)\)
Ta có: \({W_d} = 3{W_t}\) tại \(x = \pm \frac{A}{2}\)
\( \Rightarrow {t_{\min }} = 2.\frac{T}{{12}} = \frac{T}{6} = \frac{{1,2}}{6} = 0,2\left( s \right)\)
Chọn đáp án B
Câu 11:
 Xem đáp án
Xem đáp án
Chu kỳ dao động riêng của mạch: \(T = 2\pi \sqrt {LC} \Rightarrow \left( {T \sim \sqrt C } \right)\)
⇒ Điện dung C của tụ tăng thì chu kì dao động riêng của mạch cũng tăng.
Chọn đáp án A
Câu 12:
 Xem đáp án
Xem đáp án
Chu kì dao động trong mạch LC: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{{I_0}}}{{{Q_0}}}}} = \frac{{2\pi {Q_0}}}{{{I_0}}}\)
Chọn đáp án A
Câu 13:
 Xem đáp án
Xem đáp án
+ \({Z_L} = 100\Omega ;{\rm{ }}{Z_C} \approx 200\Omega \)
+ Công suất của mạch đạt cực đại khi và chỉ khi \(R = \left| {{Z_L} - {Z_C}} \right| = 100\Omega \)
Chọn đáp án C
Câu 14:
 Xem đáp án
Xem đáp án
Mạch chỉ chứa điện trở thuần ⇒ u, i cùng pha.
\( \Rightarrow i = {I_0}c{\rm{os}}(\omega t + \frac{\pi }{2})\,\,A\)
Chọn đáp án D
Câu 15:
 Xem đáp án
Xem đáp án
Chu kì dao động là khoảng thời gian ngắn nhất để trạng thái dao động lặp lại như cũ.
Chọn đáp án A
Câu 16:
 Xem đáp án
Xem đáp án
+ Chu kì của con lắc khi chưa tích điện: \(T = 2\pi \sqrt {\frac{\ell }{g}} \)
+ Khi con lắc được tích điện thì nó chịu tác dụng của lực điện trường \({\overrightarrow F _d} \uparrow \uparrow \overrightarrow P \)
+ Gia tốc trọng trường biểu kiến của con lắc đã tích điện:
\(g' = g + \frac{{{F_d}}}{m} = g + \frac{{\left| q \right|E}}{m} = 10 + \frac{{{{6.10}^{ - 5}}.4800}}{{0,08}} = 13,6\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)
+ Chu kì của con lắc sau khi được tích điện: \(T' = 2\pi \sqrt {\frac{\ell }{{g'}}} \)
\( \Rightarrow \frac{T}{{T'}} = \sqrt {\frac{{g'}}{g}} \Leftrightarrow \frac{2}{{T'}} = \sqrt {\frac{{13,6}}{{10}}} \Rightarrow T' \approx 1,71\left( s \right)\)
Chọn đáp án B
Câu 17:
 Xem đáp án
Xem đáp án
Phương trình dao động điều hòa của con lắc lò xo có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ Quỹ đạo dài 10 cm \( \Rightarrow 2A = 10 \Leftrightarrow A = 5cm\)
+ Chu kì là 1 (s) \( \Rightarrow \omega = 2\pi \left( {{\rm{rad/s}}} \right)\)
+ Tại t = 0: \[x = 0,v < 0 \Rightarrow \varphi = \frac{\pi }{2}\]
\( \Rightarrow x = 5\cos \left( {2\pi t + \frac{\pi }{2}} \right)\) (cm)
Chọn đáp án D
Câu 18:
 Xem đáp án
Xem đáp án
Ta có: \(\tan \varphi = \frac{{ - {Z_c}}}{R} \Leftrightarrow \tan \left( { - \frac{\pi }{3}} \right) = \frac{{ - {Z_c}}}{{40}} \Rightarrow {Z_C} = 40\sqrt 3 \Omega \)
Chọn đáp án A
Câu 19:
 Xem đáp án
Xem đáp án
Ta có: \(\lambda = v.T = v.2\pi \sqrt {LC} \Rightarrow \lambda \sim \sqrt {LC} \)
Để \(\frac{{\lambda '}}{\lambda } = \frac{1}{5} \Rightarrow \frac{{\sqrt {L'C'} }}{{\sqrt {LC} }} = \frac{1}{5} \Leftrightarrow \frac{{\sqrt {5L.C'} }}{{\sqrt {LC} }} = \frac{1}{5} \Rightarrow C' = \frac{C}{{125}}\)
Vậy C giảm 125 lần để thỏa mãn đề bài.
Chọn đáp án B
Câu 20:
 Xem đáp án
Xem đáp án
+ \({v_{\max }} = A\omega = 8\pi \left( {{\rm{cm/s}}} \right)\), T = 1(s)
+ Trong một chu kì, có 4 lần vật có tốc độ \(\left| v \right| = 4\pi \sqrt 3 \left( {{\rm{cm/s}}} \right)\)
+ Ta có: \({t_{2015}} = 503T + {t_3}\) với t3là thời gian vật đi qua vị trí có tốc độ \(\left| v \right| = 4\pi \sqrt 3 \left( {{\rm{cm/s}}} \right)\) lần thứ 3.
+ Tại thời điểm t = 0: \(x = 2\sqrt 3 ,v = \frac{{{v_{\max }}}}{2} = 4\pi >0\)
+ Sử dụng giản đồ vecto, ta xác định được, thời gian vật đi đến vị trí có tốc độ \(\left| v \right| = 4\pi \sqrt 3 \left( {{\rm{cm/s}}} \right)\) lần thứ 3 là:
\({t_3} = \frac{T}{{12}} + \frac{T}{2} + \frac{T}{6} = \frac{{3T}}{4}\)
Vậy \({t_{2015}} = 503T + {t_3} = 503T + \frac{{3T}}{4} = \frac{{2015}}{4}\left( s \right)\)
Chọn đáp án A
Câu 21:
 Xem đáp án
Xem đáp án
Trong dao động điều hòa, biên độ, tần số và cơ năng không thay đổi theo thời gian. Còn li độ, vận tốc, gia tốc, động năng và thế năng đều biến đổi theo thời gian.
Chọn đáp án C
Câu 22:
 Xem đáp án
Xem đáp án
Ở li độ x, vật có gia tốc là \(a = - {\omega ^2}x\)
Chọn đáp án D
Câu 23:
 Xem đáp án
Xem đáp án
Vì \(x \bot v \Rightarrow {\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1\)
Thay số vào ta được: \({\left( {\frac{2}{4}} \right)^2} + {\left( {\frac{1}{{0,04.\omega }}} \right)^2} = 1 \Rightarrow \omega = \frac{{50}}{{\sqrt 3 }}\)(rad/s)
\(\Rightarrow f \approx 4,6Hz\)
Chọn đáp án C
Câu 24:
 Xem đáp án
Xem đáp án
Trong dao động điều hòa thì véctơ vận tốc luôn cùng hướng với hướng chuyển động của vật, véctơ gia tốc luôn hướng về vị trí cân bằng.
Chọn đáp án D
Câu 25:
 Xem đáp án
Xem đáp án
Máy biến áp là thiết bị có khả năng biến đổi điện áp của dòng điện xoay chiều.
Chọn đáp án B
Câu 26:
 Xem đáp án
Xem đáp án
Trong đoạn mạch điện xoay chiều gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp thì điện áp giữa hai đầu tụ điện trễ pha so với điện áp giữa hai đầu đoạn mạch.
Chọn đáp án C
Câu 27:
 Xem đáp án
Xem đáp án
Biên độ dao động tổng hợp thỏa mãn:
\(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)
Thay số vào ta được: \(\left| {3 - 4} \right| \le A \le 3 + 4 \Leftrightarrow 1 \le A \le 7\)
Chọn đáp án A
Câu 28:
 Xem đáp án
Xem đáp án
Khi đi từ vị trí có li độ x = 0 theo chiều dương đến vị trí \[x = \frac{A}{2}\]lần thứ hai, ta có:
+ Quãng đường chất điểm đã đi được là: \(s = A + \frac{A}{2} = \frac{{3A}}{2}\)
+ Thời gian đi quãng đường trên: \(t = \frac{T}{4} + \frac{T}{6} = \frac{{5T}}{{12}}\)
⇒ Tốc độ trung bình trên đi quãng đường trên:
\({v_{tb}} = \frac{s}{t} = \frac{{\frac{{3A}}{2}}}{{\frac{{5T}}{{12}}}} = \frac{{18A}}{{5T}}\)
Chọn đáp án C
Câu 29:
 Xem đáp án
Xem đáp án
Khi hiệu điện thế giữa hai bản tụ là 9V thì năng lượng từ trường của mạch là
\({E_L} = E - {E_C} = \frac{1}{2}C\left( {U_0^2 - {u^2}} \right) = \frac{1}{2}{.4.10^{ - 6}}\left( {{{12}^2} - {9^2}} \right) = 1,{26.10^{ - 4}}J\)
Chọn đáp án C
Câu 30:
 Xem đáp án
Xem đáp án
Từ thông cực đại qua khung dây là\({\Phi _0} = NBS = 500.0,{2.54.10^{ - 4}} = 0,54Wb\).
Chọn đáp án B
Câu 31:
 Xem đáp án
Xem đáp án
Để hiệu điện thế hai đầu đoạn mạch cùng pha với hiệu điện thế hai đầu điện trở R thì trong mạch xảy ra cộng hưởng với \(\omega = \frac{1}{{\sqrt {LC} }} \Rightarrow 100\pi = \frac{1}{{\sqrt {L.\frac{{{{10}^{ - 4}}}}{\pi }} }} \Rightarrow L = \frac{1}{\pi }\left( H \right)\)
Chọn đáp án C
Câu 32:
 Xem đáp án
Xem đáp án
Công thức cảm kháng của cuộn cảm L đối với tần số f là ZL = ω.L = 2πfL
Chọn đáp án A
Câu 33:
 Xem đáp án
Xem đáp án
A – sai, sóng điện từ có thể lan truyền được trong chân không nên không cần môi trường vật chất.
B - đúng
C – đúng
D – đúng
Chọn đáp án A
Câu 34:
L = 4,5.10-6H. Chu kỳ dao động điện từ của mạch là:
 Xem đáp án
Xem đáp án
Chu kỳ dao động điện từ của mạch là:
\(T = 2\pi \sqrt {LC} = 1,{885.10^{ - 5}}\left( s \right)\)
Chọn đáp án B
Câu 35:
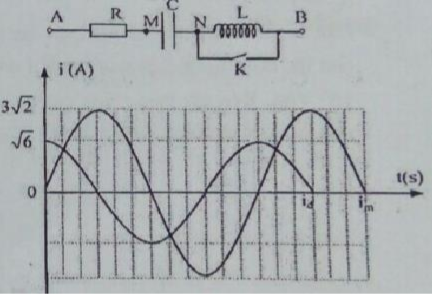
Cho mạch điện như hình vẽ, cuộn dây thuần cảm. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = 100\sqrt 6 \cos \left( {100\pi t + \varphi } \right)V\). Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là imvà idđược biểu diễn như hình bên. Điện trở các dây nối rất nhỏ. Giá trị của R bằng.
 Xem đáp án
Xem đáp án
Từ đồ thị ta thấy biểu thức cường độ dòng điện khi đóng và mở là:
\({i_m} = 3\sqrt 2 \cos \left( {\omega t - \frac{\pi }{2}} \right)\left( A \right),{\rm{ }}{i_d} = \sqrt 6 \cos \left( {\omega t} \right)\left( A \right)\)
+ Khi khóa K đóng, mạch điện chỉ gồm R mắc nối tiếp C.
\( \Rightarrow {Z_{RC}} = \sqrt {{R^2} + Z_C^2} = \frac{{{U_0}}}{{{I_{0d}}}} = \frac{{100\sqrt 6 }}{{\sqrt 6 }} = 100\Omega \)(1)
+ Khi khóa K mở, mạch điện gồm ba phần tử R, L, C mắc nối tiếp. Tổng trở được tính theo công thức \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \frac{{{U_0}}}{{{I_{0m}}}} = \frac{{100\sqrt 6 }}{{3\sqrt 2 }} = \frac{{100}}{{\sqrt 3 }}\Omega \) (2)
+ Từ biểu thức cường độ imvà idta thấy rằng hai dòng điện vuông pha với nhau, khi đó ta có \(\tan {\varphi _m}.\tan {\varphi _d} = - 1 \Leftrightarrow \frac{{{Z_C}}}{R}.\frac{{{Z_L} - {Z_C}}}{R} = 1\)
\( \Rightarrow {R^2} = {Z_C}.\left( {{Z_L} - {Z_C}} \right){\rm{ }}\left( 3 \right)\)
Thay (3) vào (1) và (2) ta giải được: \({Z_L} = \frac{{200}}{{\sqrt 3 }}\Omega ;{\rm{ }}{Z_C} = 50\sqrt 3 \Omega ;{\rm{ }}R = 50\Omega .\)
Chọn đáp án B
Câu 36:
 Xem đáp án
Xem đáp án
+ Khi đặt vào hai đầu AM một điện áp không đổi
\(I = \frac{\xi }{{{R_1} + r + {r_d}}} \Leftrightarrow 0,1875 = \frac{{12}}{{{R_1} + 4 + {r_d}}} \Rightarrow {R_1} + {r_d} = 60\Omega \) (*)
+ Dung kháng, cảm kháng của mạch khi đặt vào hai đầu đoạn mạch điện áp xoay chiều có \(\omega = 100\pi \left( {{\rm{rad/s}}} \right)\): \({Z_C} = 25\Omega ;{\rm{ }}{Z_L} = 40\Omega .\)
+ Công suất tiêu thụ của biến trở khi \(R = {R_2}\) là
\({{\rm{P}}_{\max }} = \frac{{{U^2}}}{{2\left( {{R_2} + r} \right)}} = 160{\rm{ }}\left( 1 \right)\) với \({R_2} = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{ }}\left( 2 \right)\)
+ Từ (1) và (2) \({r_d} = 20\Omega ;{\rm{ }}{R_2} = 25\Omega .\)(**)
+ Từ (*) và (**) có: \({R_1} = 40\Omega \)
Vậy \(\frac{{{R_1}}}{{{R_2}}} = \frac{{40}}{{25}} = \frac{8}{5} = 1,6\)
Chọn đáp án C
Câu 37:
 Xem đáp án
Xem đáp án
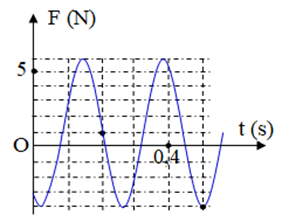
+ Từ đồ thị ta có: \(F = 1 + 5\cos \left( {\omega t + \varphi } \right) = 1 + {F_{\left( t \right)}}\left( N \right)\)
+ Tại \(t = 0,2\left( s \right)\) có \({F_{\left( t \right)}} = 0N;\) tại \(t = 0,5\left( s \right)\) có \({F_{\left( t \right)}} = - 5N\)
\( \Rightarrow 5\frac{T}{4} = 0,5 - 0,2 \Rightarrow T = 0,24s \Rightarrow \omega = \frac{{25\pi }}{3}\left( {{\rm{rad/s}}} \right)\)
+ Tại \(t = 0,2\left( s \right):{F_{\left( t \right)}} = 0\) theo chiều âm nên cần quay góc \(\alpha = \omega t = \frac{{25\pi }}{3}.0,2 = \frac{{5\pi }}{3}\) để về thời điểm ban đầu ⇒ Pha ban đầu của lực đàn hồi là \(\varphi = \frac{{5\pi }}{6}\)
+ Độ lớn của lực kéo về tại t = 0,15 s : \(\left| F \right| = \left| {5\cos \left( {\frac{{25\pi }}{3}0,15 + \frac{{5\pi }}{6}} \right)} \right| = 4,83\left( N \right)\)
Chọn đáp án D
Câu 38:
 Xem đáp án
Xem đáp án
+ Độ lệch pha giữa u và i:
\(\tan \varphi = \frac{{ - {U_C}}}{{{U_R}}} = \frac{{ - 100\sqrt 3 }}{{100}} = - \sqrt 3 \Rightarrow \varphi = {\varphi _u} - {\varphi _i} = - \frac{\pi }{3}\left( 1 \right)\)
+ Mà \({\varphi _{{u_C}}} - {\varphi _i} = - \frac{\pi }{2}\left( 2 \right)\)
+ Từ (1) và (2) \( \Rightarrow {\varphi _u} - {\varphi _{{u_C}}} = \frac{\pi }{6}\)
Chọn đáp án A
Câu 39:
 Xem đáp án
Xem đáp án
+ Chu kì dao động mạch LC: \(T = 2\pi \sqrt {LC} = 4\pi {.10^{ - 7}}\left( s \right)\)
+ Tại \({t_1}:\) \({q_1} = 0,024\mu C\) và đang phóng điện.
+ Mà q và u cùng pha nên: \({u_1} = \frac{{{q_1}}}{C} = \frac{{0,{{024.10}^{ - 6}}}}{{{{8.10}^{ - 9}}}} = 3V\)
+ Tại \({t_2} = {t_1} + \pi {.10^{ - 6}} = {t_1} + 2T + \frac{T}{2}\)\( \Rightarrow {u_1}\) và u2ngược pha, do đó \({u_2} = - 3V\)
Chọn đáp án C
Câu 40:
 Xem đáp án
Xem đáp án
O
R
ARO
BARO
θ
O
R
ARO
BARO
θ
+ Muốn vệ tinh ở trong mặt phẳng xích đạo và đứng yên so với mặt đất, nó phải chuyển động tròn xung quanh Trái Đất, cùng chiều và cùng vận tốc góc \(\omega \) như Trái Đất quay xung quanh trục của nó với chu kì T = 24h.
+ Gọi vận tốc dài của vệ tinh trên quỹ đạo là v, độ cao của nó so với mặt đất là h. Vì vệ tinh chuyển động tròn đều nên lực hướng tâm tác dụng lên vệ tinh đúng bằng lực hấp dẫn của Trái đất đối với vệ tinh.
\( \Rightarrow {F_{ht}} = {F_{hd}} \Leftrightarrow \frac{{m{v^2}}}{{\left( {R + h} \right)}} = G\frac{{M.m}}{{{{\left( {R + h} \right)}^2}}}\)
+ Mà \[v = \omega \left( {R + h} \right) = \frac{{2\pi }}{T}.\left( {R + h} \right)\]
\( \Rightarrow \frac{{{{\left( {\frac{{2\pi }}{T}.\left( {R + h} \right)} \right)}^2}}}{{\left( {R + h} \right)}} = G\frac{M}{{{{\left( {R + h} \right)}^2}}} \Rightarrow R + h = \sqrt[3]{{\frac{{GM.{T^2}}}{{4{\pi ^2}}}}} \approx {42298.10^3}\left( m \right) = 42298\left( {km} \right)\)
+ Đối với sóng cực ngắn, ta có thể xem như sóng truyền thẳng từ vệ tinh xuống mặt đất. Từ hình vẽ, ta thấy vùng nằm giữa kinh tuyến đi qua A và B sẽ nhận được tín hiệu từ vệ tinh.
+ Ta thấy: \(\cos \theta = \frac{R}{{R + h}} = \frac{{6370}}{{42298}} \Rightarrow \theta = {81^0}20'\)
+ Như vậy vùng nhận được tín hiệu từ vệ tinh nằm trong khoảng từ kinh độ 81020’T đến kinh độ 81020’Đ.
Chọn đáp án C
