Đề thi Giữa kì 1 Vật lí 12 có đáp án (Đề 1)
-
1048 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Mối quan hệ giữa các đại lượng: \[f = \frac{1}{T} = \frac{\omega }{{2\pi }}.\]
Chọn đáp án C
Câu 2:
Xem đáp án
Vận tốc tức thời trong dao động điều hòa biến đổi vuông pha với li độ.
Chọn đáp án C
Câu 3:
Xem đáp án
Lực kéo về tác dụng lên vật dao động điều hòa:
\({F_{kv}} = ma = - m{\omega ^2}x = - kx\)
⇒ Lực kéo về biến thiên điều hòa theo thời gian với cùng tần số của li độ, luôn hướng về vị trí cân bằng.
Chọn đáp án D
Câu 4:
Xem đáp án
Động năng của vật biến thiên theo thời gian với chu kì là \(\frac{T}{2}.\)
Chọn đáp án B
Câu 5:
Xem đáp án
Dao động tắt dần là dao động có cơ năng và biên độ giảm dần theo thời gian.
Chọn đáp án C
Câu 6:
Xem đáp án
Khi tần số dao động của ngoại lực bằng tần số dao động riêng của hệ dao động thì hệ xảy ra cộng hưởng, biên độ dao động đạt cực đại.
Chọn đáp án D
Câu 7:
Xem đáp án
Năng lượng đã truyền cho vật là:
\(W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,2.{\left( {4\pi } \right)^2}.0,{05^2} = 0,04J\)
Chọn đáp án D
Câu 8:
Một vật dao động điều hòa thực hiện 5 dao động trong 20 s. Chọn gốc thời gian lúc vật qua vị trí cân bằng. Thời gian ngắn nhất để vật qua vị trí có li độ cực đại kể từ lúc t = 0 là
Xem đáp án
Chu kì dao động điều hòa: \(T = \frac{t}{N} = \frac{{20}}{5} = 4\left( s \right)\)
Thời gian ngắn nhất để vật qua vị trí có li độ cực đại kể từ lúc t = 0 là
\(\frac{T}{4} = \frac{4}{4} = 1\left( s \right)\)
Chọn đáp án A
Câu 9:
Con lắc lò xo, gồm m = 200g và k = 20N/m. Kéo quả cầu m ra khỏi VTCB một đoạn 10 cm rồi buông nhẹ. Viết PT dao động, chọn gốc thời gian lúc vật có li độ 5cm và đang chuyển động ngược chiều dương.
Xem đáp án
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,2}}} = 10\left( {{\rm{rad/s}}} \right)\)
+ Kéo quả cầu m ra khỏi VTCB một đoạn 10 cm rồi buông nhẹ ⇒ A = 10 cm
+ Tại t = 0: \(x = 5cm,v < 0 \Rightarrow \varphi = \frac{\pi }{3}\)
⇒ Phương trình dao động: \[x = 10\cos \left( {10t + \frac{\pi }{3}} \right)\]
Chọn đáp án A
Câu 10:
Xem đáp án
M là điểm dao động với biên độ cực đại, giữa M và đường trung trực AB có hai dãy cực đại khác ⇒ M thuộc cực đại bậc 3
\( \Rightarrow \lambda = \frac{{{d_1} - {d_2}}}{k} = \frac{{30 - 25,5}}{3} = 1,5cm\)
Vận tốc truyền sóng trên mặt nước: \(v = \lambda .f = 1,5.16 = 24{\rm{ cm/s}}\)
Chọn đáp án B
Câu 11:
Một nguồn sóng cơ dao động điều hoà tần số 100Hz, khoảng cách giữa 7 gợn lồi liên tiếp là 9cm. Tốc độ truyền sóng là
Xem đáp án
Khoảng cách giữa 7 gợn lồi liên tiếp, tương ứng với 6λ\( \Rightarrow 6\lambda = 9 \Rightarrow \lambda = 1,5cm\)
Tốc độ truyền sóng: \(v = \lambda .f = 1,5.100 = 150{\rm{cm/s}} = 1,5{\rm{m/s}}\)
Chọn đáp án C
Câu 12:
Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là 0,4 s và 8 cm. Chọn trục x’x thẳng đứng chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian t = 0 khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10 m/s2và π2= 10. Thời gian ngắn nhất kể từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là :
Xem đáp án
+ Tần số góc của dao động: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi \left( {{\rm{rad/s}}} \right)\)
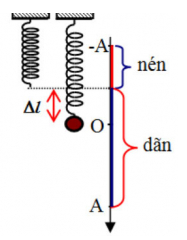
+ Độ biến dạng của con lắc lò xo khi ở vị trí cân bằng:
\(\Delta \ell = \frac{g}{{{\omega ^2}}} = \frac{\pi }{{{{\left( {5\pi } \right)}^2}}} = 0,04{\rm{ }}m = 4{\rm{ }}cm\)
+ Biên độ 8 cm
+ Nhận thấy \(\Delta \ell < A \Rightarrow {F_{d{h_{\min }}}} = 0\) tại \(x = - \Delta \ell = - 4cm\)
Thời gian ngắn nhất kể từ khi t = 0 ( x = 0; v >0) đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là:
\({t_{\min }} = \frac{T}{2} + \frac{T}{{12}} = \frac{7}{{30}}\left( s \right)\)
Chọn đáp án B
Câu 13:
Xem đáp án
Tốc độ trung bình của M trong một chu kì:
\({v_{tb}} = \frac{{4A}}{T} = \frac{{4A}}{{\frac{{2\pi }}{\omega }}} = \frac{{4.2,5}}{{\frac{{2\pi }}{{10\pi }}}} = 50\left( {{\rm{cm/s}}} \right)\)
Chọn đáp án B
Câu 14:
Xem đáp án
+ Độ biến dạng của lò xo: \(\Delta \ell = \frac{{mg}}{k} = \frac{{0,2.10}}{{20}} = 0,1m = 10cm\)
+ Biên độ dao động của con lắc lò xo: A = 5 cm
+ Lực đàn hồi cực đại: \({F_{\max }} = k\left( {\Delta \ell + A} \right) = 20.\left( {0,1 + 0,05} \right) = 3N\)
Chọn đáp án B
Câu 15:
Dao động tổng hợp của hai dao động điều hoà cùng phương x1 = 4\(\sqrt 2 \)cos(10πt+\(\frac{\pi }{3}\)) cm và x2=4\(\sqrt 2 \)cos(10πt - \(\frac{\pi }{6}\)) cm có phương trình:
Xem đáp án
Sử dụng phương trình số phức:
Dao động tổng hợp: \(x = {x_1} + {x_2} = 4\sqrt 2 \angle \frac{\pi }{3} + 4\sqrt 2 \angle - \frac{\pi }{6} = 8\angle \frac{\pi }{{12}}\)
Chọn đáp án D
Câu 16:
Xem đáp án
Biên độ dao động của con lắc: \(A = \frac{{{\ell _{\max }} - {\ell _{\min }}}}{2} = \frac{{30 - 22}}{2} = 4cm\)
Cơ năng của con lắc: \(W = \frac{1}{2}k{A^2} = \frac{1}{2}.80.0,{04^2} = 0,064J\)
Chọn đáp án D
Câu 17:
Xem đáp án
+ Chu kì con lắc đơn: \(T = 2\pi \sqrt {\frac{\ell }{k}} \left( {{T^2} \sim \ell } \right)\)
+ Ta có: \(\frac{{T_1^2}}{{T_2^2}} = \frac{{{\ell _1}}}{{{\ell _2}}} \Leftrightarrow \frac{{{\ell _1}}}{{{\ell _2}}} = \frac{{2,{4^2}}}{{1,{8^2}}} = \frac{{16}}{9}\)(1)
+ Chiều dài của con lắc ban đầu: \(\ell = {\ell _1} + {\ell _2} = 50\left( 2 \right)\)
Từ (1) và (2): \({\ell _1} = 32cm;{\rm{ }}{\ell _2} = 18cm\)
Chọn đáp án A
Câu 18:
Xem đáp án
Biên độ dao động của con lắc là: A = 3 cm
Khi quả nặng cách vị trí cân bằng đoạn 1 cm, tức là \(x = \pm 1{\rm{ }}cm\)
\( \Rightarrow \frac{{{W_t}}}{{{W_d}}} = \frac{{{W_t}}}{{W - {W_t}}} = \frac{{\frac{1}{2}k{x^2}}}{{\frac{1}{2}k\left( {{A^2} - {x^2}} \right)}} = \frac{1}{{{3^2} - 1}} = \frac{1}{8}\)
Chọn đáp án B
Câu 19:
Xem đáp án
+ Tần số góc của dao động: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{5}}} = 10\)rad/s.
+ Ta có: \(x \bot v \Rightarrow {\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1 \Leftrightarrow A = \sqrt {{x^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} \)(*)
+ Thay số vào (*) ta được: \(A = \sqrt {{2^2} + {{\left( {\frac{{20\sqrt 3 }}{{10}}} \right)}^2}} = 4\left( {cm} \right)\)
Chọn đáp án D
Câu 20:
Một con lắc đơn gồm một hòn bi nhỏ khối lượng m, treo vào một sợi dây không giãn, khối lượng dây không đáng kể. Khi con lắc đơn này dao động điều hòa với chu kì 3s thì hòn bi chuyển động trên cung tròn 4cm. Thời gian để hòn bi đi được 2cm kể từ vị trí cân bằng là
Xem đáp án
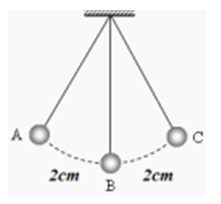
Hòn bi đi từ vị trí B (VTCB) đến vị trí C sẽ đi được 2cm.
Khoảng thời gian tương ứng là:
Chọn đáp án A.
Câu 21:
Xem đáp án
+ Thời gian ngắn nhất tính từ lúc thế năng cực đại đến động năng cực đại là
\[\Delta t = \frac{T}{4} = 0,25s \Rightarrow T = 1\left( s \right)\]
+ Với \(T = 2\pi \sqrt {\frac{m}{k}} \Rightarrow 1 = 2\pi \sqrt {\frac{{0,5}}{k}} \Rightarrow k = 20\left( {{\rm{N/m}}} \right)\)
Chọn đáp án B
Câu 22:
Một vật nặng gắn vào lò xo có độ cứng \(k = 20N/m\) dao động với biên độ A = 5cm. Chọn gốc tọa độ là vị trí cân bằng. Khi vật nặng cách vị trí cân bằng 4cm nó có động năng là
Xem đáp án
Động năng của con lắc lò xo tại vị trí có \(x = \pm 4cm\):
\({W_d} = W - {W_t} = \frac{1}{2}k\left( {{A^2} - {x^2}} \right) = \frac{1}{2}.20.\left( {0,{{05}^2} - 0,{{04}^2}} \right) = 0,009J\)
Chọn đáp án B
Câu 23:
Xem đáp án
+ Phương trình li độ:\(x = 4\cos \left( {0,5\pi t - \frac{\pi }{3}} \right)cm\)
+ Phương trình vận tốc: \(v = x' = - 4.0,5.\sin \left( {0,5\pi t - \frac{\pi }{3}} \right) = - 2\sin \left( {0,5\pi t - \frac{\pi }{3}} \right)\) (cm/s)
+ Theo đầu bài, ta có
\(\left\{ \begin{array}{l}x = 2\sqrt 3 cm\\v < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2\sqrt 3 = 4\cos \left( {0,5\pi t - \frac{\pi }{3}} \right)\\ - 2\sin \left( {0,5\pi t - \frac{\pi }{3}} \right) < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \left( {0,5\pi t - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}\left( 1 \right)\\\sin \left( {0,5\pi t - \frac{\pi }{3}} \right) >0\left( 2 \right)\end{array} \right.\)
+ Từ (1), ta được: \(\cos \left( {0,5\pi t - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2} = \cos \left( { \pm \frac{\pi }{6}} \right)\)
\( \Rightarrow 0,5\pi t - \frac{\pi }{3} = \pm \frac{\pi }{6} + 2k\pi \left( {k \in Z} \right)\)
Trường hợp 1: Với \(0,5\pi t - \frac{\pi }{3} = \frac{\pi }{6} + 2k\pi \Rightarrow t = 1 + 4k\)
Vì t >0 nên 1 + 4k >0 ⇒ k >- 0,25 ⇒ k = 0, 1, 2, 3, 4, ...
Khi k = 0 ⇒ t = 1(s)
Thay t = 1(s) vào (2) thấy \(\sin \left( {0,5\pi .1 - \frac{\pi }{3}} \right) = \frac{1}{2} >0\) (thỏa mãn)
(Không xét tiếp với các giá trị khác của k vì ta thấy tất cả các giá trị khác của k đều cho t >2 không có trong phần đáp án)
Trường hợp2: Với \(0,5\pi t - \frac{\pi }{3} = - \frac{\pi }{6} + 2k\pi \Rightarrow t = \frac{1}{3} + 4k\)
Vì t >0 nên \(\frac{1}{3} + 4k >0 \Rightarrow k >- \frac{1}{{12}} \Rightarrow k = 0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}4,{\rm{ }}...\)
Khi k = 0 ⇒ \(t = \frac{1}{3}\) (s)
Thay \(t = \frac{1}{3}\) (s) vào (2) thấy \(\sin \left( {0,5\pi .\frac{1}{3} - \frac{\pi }{3}} \right) = - \frac{1}{2} < 0\) (Không thỏa mãn)
(Không xét tiếp với các giá trị khác của k vì ta thấy tất cả các giá trị khác của k đều cho t >2 không có trong phần đáp án)
Chọn đáp án A
Câu 24:
Xem đáp án
+ Chu kì dao động điều hòa: \(T = 1\left( s \right)\)
+ Tại thời điểm t: x1= 3 cm, v >0.
+ Tại thời điểm t + 0,25 s = \(t + \frac{T}{4}\), ta có: \({A^2} = x_1^2 + x_2^2 \Rightarrow {x_2} = 4cm\)
Chọn đáp án B
Câu 25:
Xem đáp án
+ Độ biến dạng của lò xo: \(\Delta \ell = 22,5 - 20 = 2,5cm\)
+ Độ cứng của lò xo: \(k = \frac{{mg}}{{\Delta \ell }} = \frac{{0,1.10}}{{0,025}} = 40{\rm{N/m}}\)
+ Khi lò xo có chiều dài 24,5 cm, ứng với \(x = 24,5 - 22,5 = 2cm\)
+ Thế năng của con lắc tại vị trí có \(x = 2cm:{W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}.40.0,{02^2} = 0,008J\)
Chọn đáp án D