 Giải bởi Vietjack
Giải bởi Vietjack
a) TXĐ: R
y′ = 0 ⇔ x = 64
Bảng biến thiên:
Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
b) Hàm số xác định trên khoảng (−∞;+∞).
Bảng biến thiên:
Vậy yCD = y(−2) =
c) Hàm số xác định trên khoảng (−√10;√10).
Vì y’ > 0 với mọi (−√10;√10) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
d) TXĐ: D = (−∞; −√6) ∪ (√6; +∞)
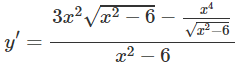
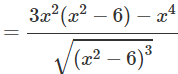
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = -3 và yCT = y(3) = 9√3; yCD = y(−3) = −9√3
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Xác định giá trị của tham số m để hàm số sau không có cực trị
y =
Tìm cực trị của các hàm số sau:
a) y = −2x2 + 7x − 5
b) y = x3 − 3x2 − 24x + 7
c) y = (x + 2)2.(x − 3)3
Xác định giá trị của tham số m để hàm số y = x3 – 2x2 + mx + 1 đạt cực tiểu tại x = 1. (Đề thi tốt nghiệp THPT năm 2011)
Xác định giá trị của tham số m để hàm số sau có cực trị:
y = x3 + 2mx2 + mx − 1
Xác định m để hàm số: y = x3 − mx2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Tìm cực trị của các hàm số sau:
a) y = sin2x
b) y = cosx − sinx
c) y = sin2x
Xác định giá trị của tham số m để hàm số y = x3 - 3x2 + mx - 5 có cực trị:
Cho hàm số:
Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:
Xác định giá trị của tham số m để hàm số sau có cực trị
y = x3 - 3(m - 1)x2 - 3(m + 3)x - 5
Chứng minh rằng hàm số:
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.