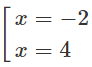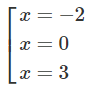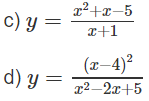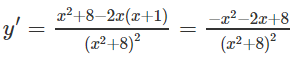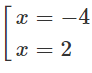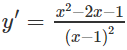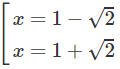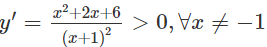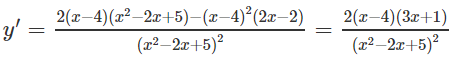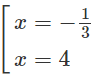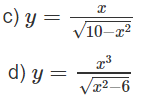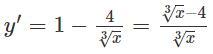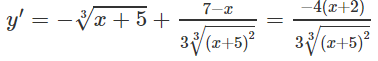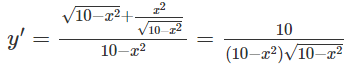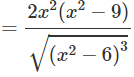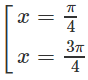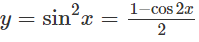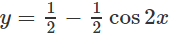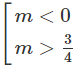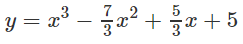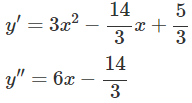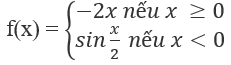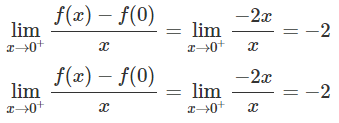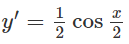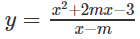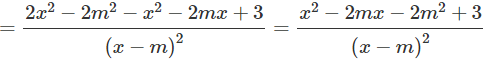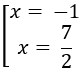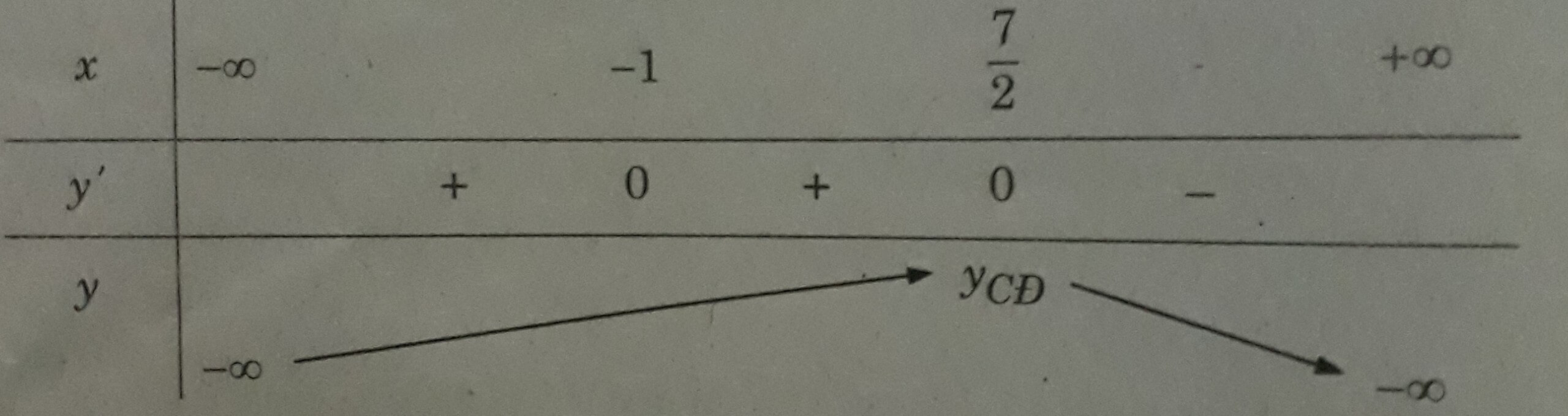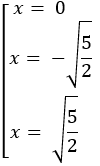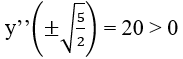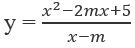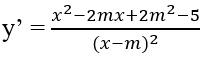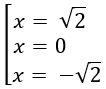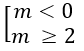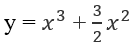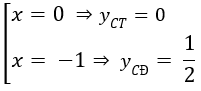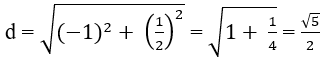Giải SBT Toán 12 Giải tích - Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Giải sbt Giải tích 12 Bài 2: Cực trị của hàm số
-
1081 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm cực trị của các hàm số sau:
a) y = −2x2 + 7x − 5
b) y = x3 − 3x2 − 24x + 7
c) y = (x + 2)2.(x − 3)3
 Xem đáp án
Xem đáp án
a) y = −2x2 + 7x − 5. TXĐ: R
y′ = −4x + 7, y′ = 0 ⇔ x = 7/4
y′′ = −4 ⇒ y′′(7/4) = −4 < 0
Vậy x = 7/4 là điểm cực đại của hàm số và yCD = 9/8
b) y = x3 − 3x2 − 24x + 7. TXĐ: R
y′ = 3x2 − 6x – 24 = 3(x2 − 2x − 8)
y′ = 0 ⇔
Vì y′′(−2) = −18 < 0, y′′(4) = 18 > 0 nên hàm số đạt cực đại tại x = -2; đạt cực tiểu tại x = 4 và yCĐ = y(-2) = 35; yCT = y(4) = -73.
e) TXĐ: R
y′ = 2(x + 2).(x − 3)3 + 3(x + 2)2.(x − 3)2 = 5x(x + 2).(x − 3)2
y′= 0 ⇔
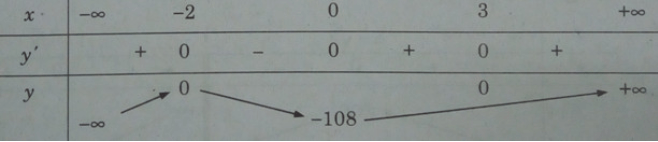
Bảng biến thiên:
Từ đó suy ra yCĐ = y(-2) = 0; yCT = y(0) = -108.
Câu 2:
Tìm cực trị của các hàm số sau:
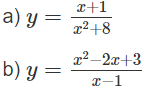
 Xem đáp án
Xem đáp án
a) TXĐ : R
y′= 0 ⇔
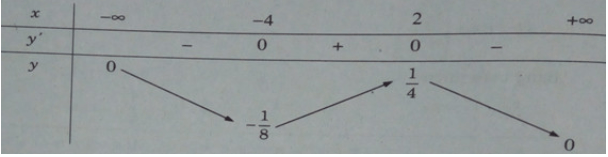
Bảng biến thiên:
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và yCD = y(2) = 1/4;
yCT = y(−4) = −1/8
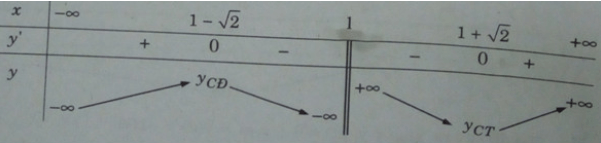
b) Hàm số xác định và có đạo hàm với mọi x ≠ 1.
y′=0 ⇔
Bảng biến thiên:
Hàm số đạt cực đại tại x = 1 − √2 và đạt cực tiểu tại x = 1 + √2, ta có:
yCD = y(1 − √2) = −2√2;
yCT = y(1 + √2) = 2√2.
c) TXĐ: R\{-1}
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
d) Vì x2 – 2x + 5 luôn luôn dương nên hàm số xác định trên (−∞; +∞)
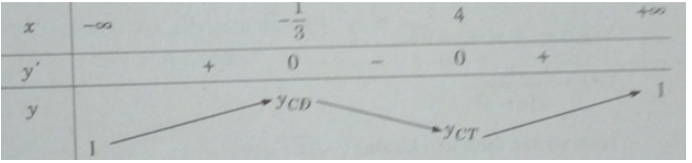
y′ = 0 ⇔
Bảng biến thiên:
Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và yCD = y(−1/3) = 13/4; yCT = y(4) = 0
Câu 3:
Tìm cực trị của các hàm số sau:
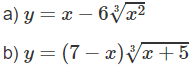
 Xem đáp án
Xem đáp án
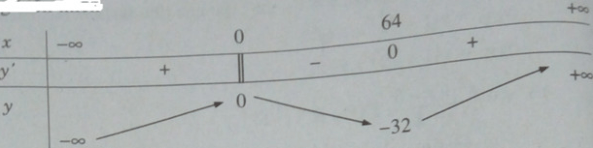
a) TXĐ: R
y′ = 0 ⇔ x = 64
Bảng biến thiên:
Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
b) Hàm số xác định trên khoảng (−∞;+∞).
Bảng biến thiên:
Vậy yCD = y(−2) =
c) Hàm số xác định trên khoảng (−√10;√10).
Vì y’ > 0 với mọi (−√10;√10) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
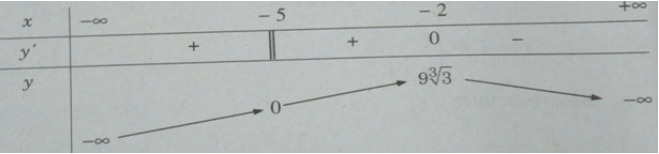
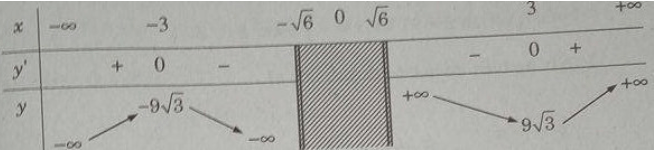
d) TXĐ: D = (−∞; −√6) ∪ (√6; +∞)
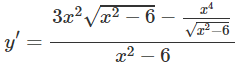
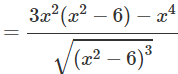
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = -3 và yCT = y(3) = 9√3; yCD = y(−3) = −9√3
Câu 4:
Tìm cực trị của các hàm số sau:
a) y = sin2x
b) y = cosx − sinx
c) y = sin2x
 Xem đáp án
Xem đáp án
a) y = sin2x
Hàm số có chu kỳ T = π
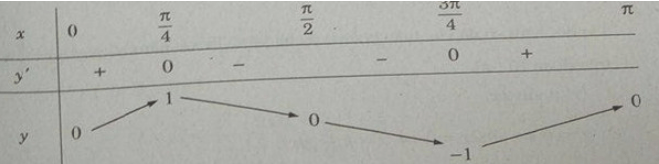
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔
Bảng biến thiên:
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và yCD = y(π/4) = 1; yCT = y(3π/4) = −1
Vậy trên R ta có:
yCĐ = y(π/4 + kπ) = 1;
yCT = y(3π/4 + kπ) = −1, k∈Z
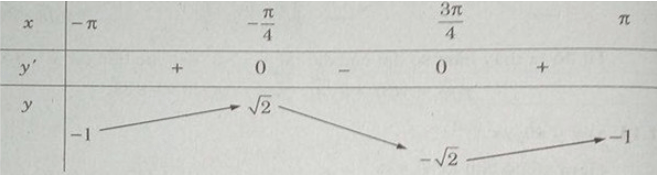
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
yCĐ = y(−π4 + k2π) = √2;
yCT = y(3π4 + k2π) = −√2 (k∈Z).
c) Ta có:
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
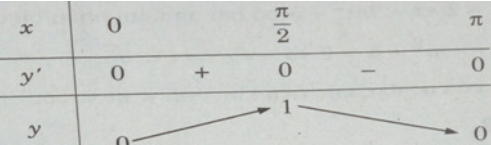
Ta xét hàm số y trên đoạn [0;π]:
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
yCT = y(2mπ) = 0; yCT = y(2mπ) = 0;
yCĐ = y((2m+1)π/2) = 1 (m∈Z)
Câu 5:
Xác định giá trị của tham số m để hàm số sau có cực trị:
y = x3 + 2mx2 + mx − 1
 Xem đáp án
Xem đáp án
TXĐ: D = R
y’ = 3x2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3x2 + 4mx + m có hai nghiệm phân biệt.
⇔ Δ’ = 4m2 -3m > 0 ⇔ m(4m – 3) > 0
⇔
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.
Câu 6:
Xác định giá trị của tham số m để hàm số y = x3 – 2x2 + mx + 1 đạt cực tiểu tại x = 1. (Đề thi tốt nghiệp THPT năm 2011)
 Xem đáp án
Xem đáp án
TXĐ: D = R
y’ = 3x2 – 4x + m; y’ = 0 ⇔ 3x2 – 4x + m = 0
Phương trình trên có hai nghiệm phân biệt khi:
∆’ = 4 – 3m > 0 ⇔ m < 4/3 (∗)
Hàm số có cực trị tại x = 1 thì :
y’(1) = 3 – 4 + m = 0 ⇒ m = 1 (thỏa mãn điều kiện (∗) )
Mặt khác, vì:
y’’ = 6x – 4 ⇒ y’’(1) = 6 – 4 = 2 > 0
cho nên tại x = 1, hàm số đạt cực tiểu.
Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1
Câu 7:
Xác định m để hàm số: y = x3 − mx2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
 Xem đáp án
Xem đáp án
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3x2 − 2mx + (m – 2/3)
Δ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành
Ta có:
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và yCT = y(1) = (16/3).
Câu 8:
Chứng minh rằng hàm số:
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
 Xem đáp án
Xem đáp án
Hàm số:
Không có đạo hàm tại x = 0 vì:
Mặt khác, với x < 0 thì
với x > 0 thì y’ = -2 < 0
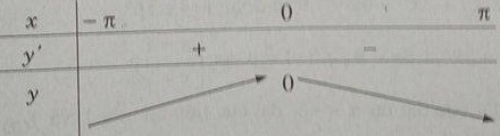
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 0.
Câu 9:
Xác định giá trị của tham số m để hàm số sau không có cực trị
 Xem đáp án
Xem đáp án
Hàm số không có cực trị khi đạo hàm của nó không đổi dấu trên tập xác định R\{m}.
Ta có:
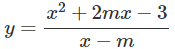
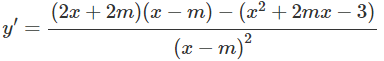
Xét g(x) = x2 – 2mx – 2m2 + 3
Δ’g = m2 + 2m2 – 3 = 3(m2 – 1) ;
Δ’g ≤ 0 khi – 1 ≤ m ≤ 1.
Khi – 1 ≤ m ≤ 1 thì phương trình g(x) = 0 vô nghiệm hay y’ = 0 vô nghiệm và y’ > 0 trên
tập xác định. Khi đó, hàm số không có cực trị.
Khi m = 1 hoặc m = -1, hàm số đã cho trở thành y = x + 3 (với x ≠ 1) hoặc y = x – 3 (với x ≠ - 1) Các hàm số này không có cực trị.
Vậy hàm số đã cho không có cực trị khi – 1 ≤ m ≤ 1.
Câu 10:
Hàm số y = (x + 1)3(5 - x) có mấy điểm cực trị?
 Xem đáp án
Xem đáp án
Đáp án: B.
Hàm số y = (x + 1)3(5 - x) xác định trên R.
y' = -(x + 1)3 + 3(x + 1)2(5 - x) = 2(x + 1)2(7 - 2x)
y' = 0 ⇔
Bảng biến thiên
Suy ra hàm số chỉ có một cực trị (là cực đại)
Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị
Câu 11:
Hàm số y = x4 - 5x2 + 4 có mấy điểm cực đại?
 Xem đáp án
Xem đáp án
Đáp án: D.
Hàm số y = x4 - 5x2 + 4 xác định trên R.
y' = 4x3 - 10x = 2x(2x5 - 5);
y' = 0 khi
y'' = 12x2 - 10
Vì y''(0) = -10 < 0,
nên hàm số chỉ có một cực đại (tại x = 0)
Cách khác: Vì a > 0 và y' = 0 có ba nghiệm phân biệt nên hàm số
y = ax4 + bx2 + c có một cực đại
Câu 12:
Xác định giá trị của tham số m để hàm số y = x3 - 3x2 + mx - 5 có cực trị:
 Xem đáp án
Xem đáp án
Đáp án: C.
Tập xác định: D = R. y' = 3x2 - 6x + m.
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên R
⇔ 3x2 - 6x + m = 0 có hai nghiệm phân biệt
⇔ Δ' = 9 - 3m > 0 ⇔ 3m < 9 ⇔ m < 3
Câu 13:
Xác định giá trị của tham số m để hàm số có cực trị:
 Xem đáp án
Xem đáp án
Đáp án: D.
Tập xác định: D = R \ {m}
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên D
⇔ x2 - 2mx + 2m2 - 5 = 0 có hai nghiệm phân biệt
⇔ Δ' = -m2 + 5 > 0 ⇔ -√5 < m < √5
Câu 14:
Cho hàm số y = -x4 + 4x2 - 3. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án: B.
Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = ax4 + bx2 + c có hai cực đại, một cực tiểu.
Ở đây y' = -4x3 + 8x; y' = 0 ⇔ -4x(x2 - 2) = 0
⇔
Câu 15:
Xác định giá trị của tham số m để hàm số sau không có cực trị
y =
 Xem đáp án
Xem đáp án
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = mx2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m2 - 2m(m - 1) = -m2 + 2m ≤ 0
⇔
Câu 16:
Xác định giá trị của tham số m để hàm số sau có cực trị
y = x3 - 3(m - 1)x2 - 3(m + 3)x - 5
 Xem đáp án
Xem đáp án
Đáp án: B.
Hàm số đã cho có cực trị khi và chỉ khi
y' = 3x2 - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt
⇔ Δ' = (m - 1)2 + (m + 3) = m2 - m + 4 > 0
Ta thấy tam thức Δ' = m2 - m + 4 luôn dương với mọi m vì
δ = 1 - 16 = -15 < 0, a = 1 > 0
Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R
Câu 17:
Cho hàm số:
Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Đáp án: D.
y' = 3x2 + 3x = 3x(x + 1) = 0
⇔
Vậy khoảng cách giữa hai điểm cực trị là: