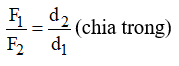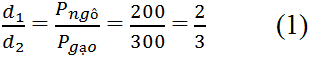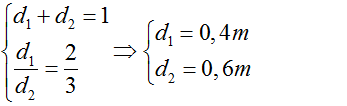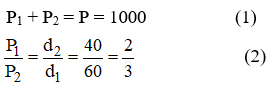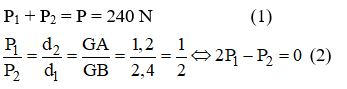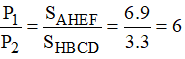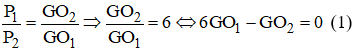Bài 19 : Quy tắc hợp lực song song cùng chiều
-
2137 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phát biểu qui tắc tổng hợp hai lực song song cùng chiều.
Xem đáp án
+ Hợp lực của hai lực song song cùng chiều là một lực song song, cùng chiều và có độ lớn bằng tổng các độ lớn của hai lực ấy.
+ Giá của hợp lực chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy.
F = F1 + F2
Câu 2:
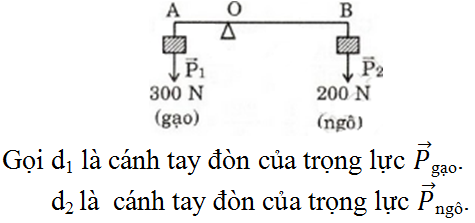
Một người gánh một thùng gạo nặng 300 N và một thùng ngô nặng 200 N. Đòn gánh dài 1 m. Hỏi vai người đó phải đặt ở điểm nào, chịu một lực bằng bao nhiêu? Bỏ qua trọng lực của đòn gánh.
Xem đáp án
Hình biểu diễn lực:
Áp dụng quy tắc hợp lực hai lực song song cùng chiều:
Mặt khác ta có:
d1 + d2 = AB = 1 m (2)
Từ (1), (2) ta có hệ phương trình sau:
Vai người gánh chịu một lực là:
P = Pgạo + Pngô = 300 + 200 = 500 (N).
Câu 3:
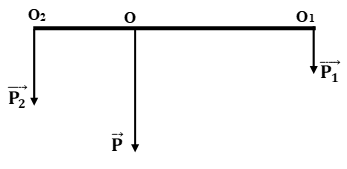
Hai người dùng một chiếc gậy để khiêng một cỗ máy nặng 1000 N. Điểm treo cỗ máy cách vai người đi trước 60 cm và cách vai người đi sau 40 cm. Bỏ qua trọng lượng của gậy, hỏi mỗi người chịu một lực bằng bao nhiêu?
Xem đáp án
Gọi P1 là lực tác dụng lên vai người đi trước, P2 là lực tác dụng lên vai người đi sau, ta đã có: d1 = OO1 = 60 cm; d2 = OO2 = 40 cm.
Áp dụng quy tắc hợp lực hai lực song song cùng chiều ta được:
Giải hệ (1) và (2) ta được: P1 = 400 N, P2 = 600 N
Câu 4:
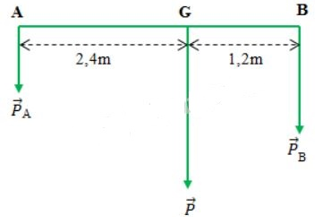
Một tấm ván nặng 240 N được bắc qua một con mương. Trọng tâm của tấm ván cách điểm tựa A 2,4 m và cách điểm tựa B 1,2 m. Hỏi lực mà tấm ván tác dụng lên điểm tựa A bằng bao nhiêu?
Xem đáp án
Chọn B.
Biểu diễn lực như hình vẽ sau:
Giải hệ (1) và (2) ta được: P1 = 80 N; P2 = 160 N.
Câu 5:
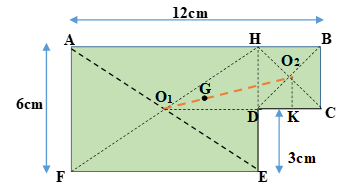
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình 19.7).
Xem đáp án
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
Gọi G là trọng tâm của cả bản phẳng ⇒ G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
Xét tam giác vuông O1O2K ta có:
Giải hệ (1) và (2) ta được: GG1 ≈ 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.