Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới
Giải Toán lớp 10 Bài tập cuối chương 2
Bài 2.16 trang 32 Toán 10 tập 1: Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.
Đài phát thanh chỉ nhận được quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây với chi phí là 80 nghìn đồng/giây. Đài truyền hình chỉ nhận được các quảng cáo có tổng thời lượng tối đa trong một tháng tối đa là 360 giây với chi phí là 400 nghìn đồng/giây. Công ty cần đặt thời gian quảng cáo trên các đài phát thanh và truyền hình như thế nào để hiệu quả nhất?
Gợi ý: Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài phát thanh và y (giây) trên truyền hình là F(x; y) = x + 8y. Ta cần tìm giá trị lớn nhất của hàm F(x; y) với x, y thỏa mãn các điều kiện trong đề bài.
Lời giải
Gọi x (giây) là thời lượng quảng cáo trong một tháng công ty đặt trên đài truyền hình và y (giây) là thời lượng quảng cáo trong một tháng công ty đặt trên đài phát thanh. (0 ≤ x ≤ 360, 0 ≤ y ≤ 900).
Chi phí công ty chi trả cho quảng cáo trong một tháng là: 400x + 80y (nghìn đồng)
Vì công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới nên ta có:
400x + 80y ≤ 160 000 hay 5x + y ≤ 2 000.
Khi đó ta có hệ bất phương trình:
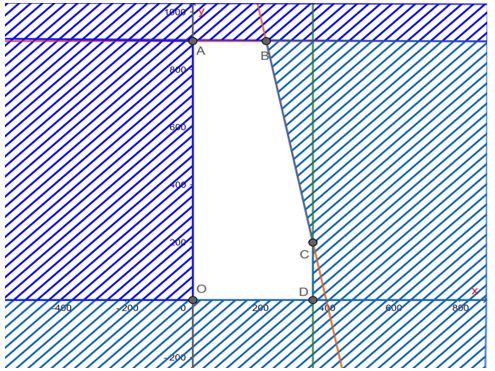
Miền nghiệm của hệ bất phương trình là ngũ giác OABCD với tọa độ các điểm là O(0;0), A(0;900), B(220;900), C(360;200), D(360;0).
Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài truyền hình và y (giây) trên đài phát thanh là F(x; y) = 8x + y.
Tính giá trị F(x; y) tại các điểm O, A, B, C, D, ta có:
Ta có: F(0; 0) = 8.0 + 0 = 0;
F(0; 900) = 8.0 + 900 = 900;
F(220; 900) = 8.220 + 900 = 2 660;
F(360; 200) = 8.360 + 200 = 3 080.
F(360; 0) = 8.360 + 0 = 2 880.
Suy ra F(x; y) đạt giá trị lớn nhất bằng 3 080 tại x = 360, y = 200.
Vậy công ty cần đặt thời gian quảng cáo 200 giây trên đài phát thanh và 360 giây trên đài truyền hình để đạt hiệu quả cao nhất.
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Bài 2.7 trang 31 Toán 10 tập 1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn...
