Giải SGK Vật lí 11 KNTT Bài 4. Bài tập về dao động điều hoà có đáp án
-
131 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Khi biết phương trình hoặc đồ thị của vật dao động điều hoà, làm thế nào để xác định được vận tốc và gia tốc của vật?
 Xem đáp án
Xem đáp án
Khi biết phương trình của dao động điều hoà ta có thể sử dụng phương pháp đạo hàm để xác định được vận tốc, gia tốc của vật hoặc có thể xác định các đại lượng đặc trưng của dao động điều hoà và sử dụng các công thức đã biết để tính.
Câu 2:
Nếu đề bài cho phương trình dao động không đúng dạng cơ bản thì ta xác định pha ban đầu như thế nào?
 Xem đáp án
Xem đáp án
Ta phải đưa về phương trình chính tắc có đúng dạng , sau đó xác định pha ban đầu .
Câu 3:
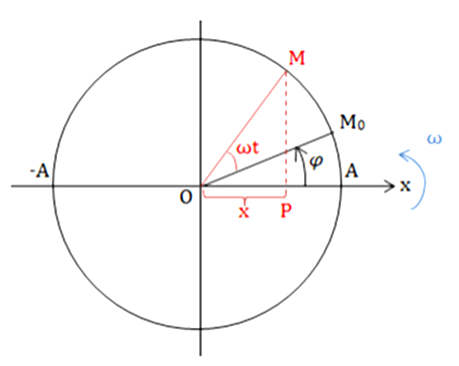
Có thể sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều để xác định pha ban đầu, thời gian để vật đi từ điểm này đến điểm khác trong dao động điều hoà được không?
 Xem đáp án
Xem đáp án
Hoàn toàn có thể sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều để xác định pha ban đầu, thời gian để vật đi từ điểm này đến điểm khác trong dao động điều hoà.
Câu 6:
Hình 4.2 là sơ đồ của một bàn xoay hình tròn, có gắn một thanh nhỏ cách tâm bàn 15 cm. Bàn xoay được chiếu sáng bằng nguồn sáng rộng, song song, hướng chiếu sáng từ phía trước màn để bóng đổ lên màn hình. Một con lắc đơn dao động điều hoà phía sau bàn xoay với biên độ bằng khoảng cách từ thanh nhỏ đến tâm bàn xoay. Tốc độ quay của bàn quay được điều chỉnh là rad/s. Vị trí bóng của thanh nhỏ con lắc luôn trùng nhau.
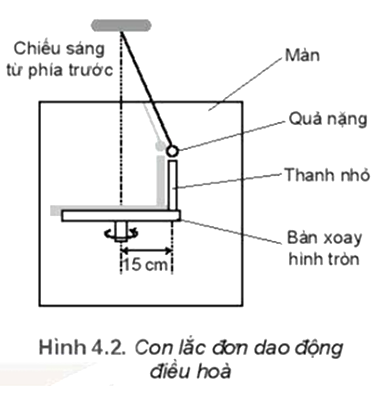
a) Tại sao nói dao động của bóng của thanh nhỏ và quả nặng là đồng pha?
b) Viết phương trình dao động của con lắc. Chọn gốc thời gian là lúc con lắc ở vị trí hiển thị trong Hình 4.2.
c) Bàn xoay đi một góc 60° từ vị trí ban đầu, tính li độ của con lắc và tốc độ của nó tại thời điểm này.
 Xem đáp án
Xem đáp án
a) Do vị trí của con lắc và bóng của thanh nhỏ luôn trùng nhau nên ta nói dao động của chúng là đồng pha.
b) Gốc thời gian là lúc con lắc ở vị trí biên dương và đang tiến về VTCB nên pha ban đầu là và biên độ A = 15 cm.
Tốc độ quay của bàn là rad/s nên tốc độ góc của con lắc đơn cũng là rad/s.
Phương trình dao động của con lắc đơn:
c) Bàn xoay đi một góc 60° từ vị trí ban đầu, tương đương với pha dao động của con lắc đơn khi đó là 60°, li độ của con lắc đơn:
Tốc độ của con lắc đơn tại thời điểm này:
Câu 7:
Hình 4.3 là đồ thị li độ – thời gian của một vật dao động điều hoà.
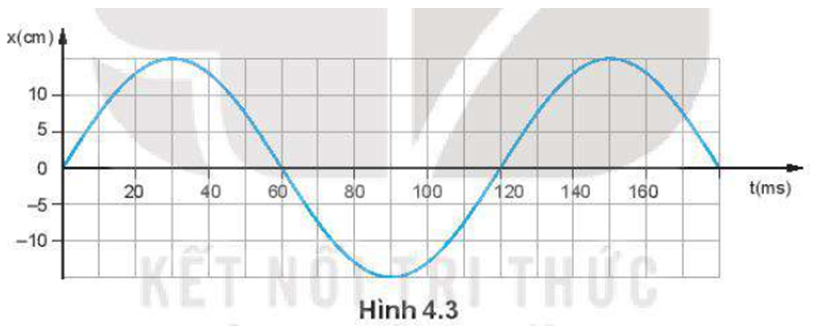
a) Xác định biên độ, chu kì, tần số, tần số góc và pha ban đầu của vật dao động.
b) Viết phương trình của dao động của vật.
 Xem đáp án
Xem đáp án
a) Biên độ: A = 15 cm
Chu kì: T = 120 ms
Tần số:
Tần số góc:
Tại thời điểm ban đầu vật xuất phát từ VTCB và đi theo chiều dương nên pha ban đầu .
b) Phương trình dao động của vật:
Câu 8:
Đồ thị li độ – thời gian của hai vật dao động điều hoà A và B có cùng tần số nhưng lệch pha nhau Hình 4.4.

a) Xác định li độ dao động của vật B khi vật A có li độ cực đại và ngược lại.
b) Hãy cho biết vật A hay vật B đạt tới li độ cực đại trước.
c) Xác định độ lệch pha giữa dao động của vật A so với dao động của vật B.
 Xem đáp án
Xem đáp án
a) Khi A có li độ cực đại thì B có li độ bằng 0.
Khi B có li độ cực đại thì A có li độ bằng 0.
b) Hai dao động này có cùng chu kì T = 60 ms, cùng biên độ A = 20 cm.
Từ đồ thị có thể thấy:
+ Tại t = 0 vật A ở VTCB và dịch chuyển về phía x > 0.
+ Tại t = 0 vật B ở vị trí biên âm và dịch chuyển về VTCB.
Như vây, để đạt li độ cực đại tiếp theo thì dao động A sẽ đạt tới li độ cực đại trước dao động B.
c) Tại thời điểm ban đầu dao động A xuất phát từ VTCB theo chiều dương nên:
Tại thời điểm ban đầu dao động B xuất phát từ biên âm theo chiều dương nên:
Độ lệch pha của hai dao động: nên dao động B trễ pha hơn dao động A góc .


