Chứng minh các hệ thức sau: sin^2 α + cos^2 α = 1

Lời giải Bài 3.3 trang 37 Toán 10 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.

506 lượt xem

« Trang trước

Trang sau »

Giải Toán lớp 10 Bài 5: Giá trị lượng giác của một góc từ 0^o đến 180^o

Bài 3.3 trang 37 Toán 10 tập 1: Chứng minh các hệ thức sau:

a) sin² α + cos² α = 1;

b) $1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ (α ≠ 90^o);

c) 2 $1 + \cot^{2} α = \frac{1}{\sin^{2} α}$ (0^o < α < 180^o).

Lời giải:

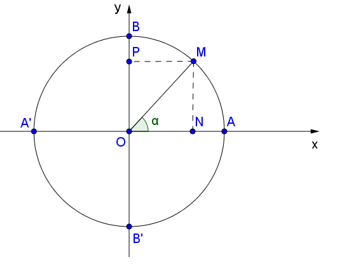
Chứng minh các hệ thức sau: sin^2 α + cos^2 α = 1 (ảnh 1)

Gọi M(x; y) là điểm trên đường tròn đơn vị sao cho $\hat{x O M} = α$ .

Ta có: OM = 1 (bán kính đường tròn đơn vị).

Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: $\{\begin{cases} x = \cos α \\ y = \sin α \end{cases} \Rightarrow \{\begin{cases} x^{2} = \cos^{2} α \\ y^{2} = \sin^{2} α \end{cases}$ (1)

Mà $\{\begin{cases} |x| = O N \\ |y| = O P = M N \end{cases} \Rightarrow \{\begin{cases} x^{2} = {|x|}^{2} = O N^{2} \\ y^{2} = {|y|}^{2} = M N^{2} \end{cases}$ (2)

Từ (1) và (2) suy ra: sin² α + cos² α = ON² + MN² = OM² = 1 (do ∆OMN vuông tại N).

Do đó sin² α + cos² α = 1 (đpcm).

b) Ta có: $\tan α = \frac{\sin α}{\cos α}$ (α ≠ 90^o)

$1 + \tan^{2} α = 1 + \frac{\sin^{2} α}{\cos^{2} α}$

$= \frac{\cos^{2} α}{\cos^{2} α} + \frac{\sin^{2} α}{\cos^{2} α} = \frac{\cos^{2} α + \sin^{2} α}{\cos^{2} α}$ .

Mà theo câu a) ta có: sin² α + cos² α = 1 với mọi góc α.

$1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ (đpcm)

c) Ta có: $\cot α = \frac{\cos α}{\sin α}$ (0^o < α < 180^o)

$1 + \cot^{2} α = 1 + \frac{\cos^{2} α}{\sin^{2} α}$

$= \frac{\sin^{2} α}{\sin^{2} α} + \frac{\cos^{2} α}{\sin^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\sin^{2} α}$ .

Mà theo câu a) ta có: sin² α + cos² α = 1 với mọi góc α.

$1 + \cot^{2} α = \frac{1}{\sin^{2} α}$ (đpcm).

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Mở đầu trang 33 Toán 10 tập 1: Bạn đã biết tỉ số lượng giác của 1 góc nhọn. Đối với góc tù thì sao?...

HĐ 1 trang 34 Toán 10 tập 1: Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau...

Luyện tập 1 trang 35 Toán 10 tập 1: Tìm các giá trị lượng giác của góc 120o (H.3.4)...

HĐ 2 trang 36 Toán 10 tập 1: Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy...

Luyện tập 2 trang 36 Toán 10 tập 1: Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau...

Vận dụng trang 37 Toán 10 tập 1: Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m...

Bài 3.1 trang 37 Toán 10 tập 1: Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau...

Bài 3.2 trang 37 Toán 10 tập 1: Đơn giản các biểu thức sau...

Bài 3.3 trang 37 Toán 10 tập 1: Chứng minh các hệ thức sau...

Bài 3.4 trang 37 Toán 10 tập 1: Cho góc α (0o < α < 180o) thỏa mãn tan α = 3...

Bài viết liên quan

506 lượt xem

« Trang trước

Trang sau »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Chứng minh các hệ thức sau: sin^2 α + cos^2 α = 1

Bài viết liên quan

Có thể bạn quan tâm