Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4)

Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4)

Lời giải Bài 4.24 trang 70 Toán 10 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.

189 lượt xem

« Trang trước

Trang sau »

Giải Toán lớp 10 Bài 11: Tích vô hướng của hai vecto

Bài 4.24 trang 70 Toán 10 tập 1: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4), C(2; ‒2).

a) Giải tam giác ABC.

b) Tìm tọa độ trực tâm H của tam giác ABC.

Lời giải

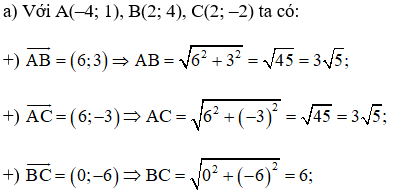
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4) (ảnh 1)

+) Theo định lí cosin, ta có:

$cos A = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{{(3 \sqrt{5})}^{2} + {(3 \sqrt{5})}^{2} - 6^{2}}{2.3 \sqrt{5} .3 \sqrt{5}} = \frac{54}{90} = \frac{3}{5}$

$\Rightarrow \hat{A} \approx 53 ° 8'$

Tam giác ABC có AB = AC nên tam giác ABC cân tại A

$\Rightarrow \hat{B} = \hat{C} = \frac{180^{0} - \hat{A}}{2} \approx \frac{180 ° - 53 ° 8'}{2} = 63 ° 26'$ .

Vậy: $A B = A C = 3 \sqrt{5}, B C = 6, \hat{A} \approx 53 ° 8', \hat{B} = \hat{C} \approx 63 ° 26' .$

b) Giả sử trực tâm H của tam giác ABC có tọa độ là H(x; y).

Do H là trực tâm của tam giác ABC nên $A H ⊥ B C; B H ⊥ A C$ $\Leftrightarrow \vec{A H} ⊥ \vec{B C}; \vec{B H} ⊥ \vec{A C}$

Với A(‒4; 1), B(2; 4), C(2; ‒2) và H(x; y) ta có:

$\vec{A H} = (x + 4; y - 1); \vec{B C} = (0; - 6); \vec{B H} = (x - 2; y - 4); \vec{A C} = (6; - 3)$

Vì $\vec{A H} ⊥ \vec{B C}$ nên $\vec{A H} . \vec{B C} = 0$ $\Leftrightarrow$ (x + 4).0 + (y – 1).(‒6) = 0 $\Leftrightarrow$ ‒6.(y – 1) = 0 $\Leftrightarrow$ y = 1.

Vì $\vec{B H} ⊥ \vec{A C}$ nên $\vec{B H} . \vec{A C} = 0$ Û (x – 2).6 + (y – 4).(‒3) = 0

(x – 2).2 + (y – 4).(‒1) = 0 Û 2x – y = 0.

Mà y = 1 $\Rightarrow 2 x - 1 = 0 \Leftrightarrow x = \frac{1}{2} .$

Vậy toạ độ trực tâm H của tam giác ABC là $H (\frac{1}{2}; 1)$ .

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

HĐ 1 trang 66 Toán 10 tập 1: Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ $\vec{A B}$ và $\vec{A C}$ ...

Câu hỏi trang 66 Toán 10 tập 1: Khi nào thì góc giữa hai vectơ bằng 0^°, bằng 180^°....

Luyện tập 1 trang 66 Toán 10 tập 1: Cho tam giác đều ABC. Tính $(\vec{A B}, \vec{B C}) .$ ..

Câu hỏi trang 67 Toán 10 tập 1: Khi nào tích vô hướng của hai vectơ khác vectơ-không $\vec{u}, \vec{v}$ là một số dương...

Câu hỏi trang 67 Toán 10 tập 1: Khi nào thì ${(\vec{u} . \vec{v})}^{2} = {\vec{u}}^{2} . {\vec{v}}^{2} ?$ ...

Luyện tập 2 trang 67 Toán 10 tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c...

HĐ 2 trang 68 Toán 10 tập 1: Cho hai vectơ cùng phương $\vec{u} = (x; y)$ và $\vec{v} = (k x; k y) .$ ..

HĐ 3 trang 68 Toán 10 tập 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương $\vec{u} = (x; y)$ ...

Luyện tập 3 trang 68 Toán 10 tập 1: Tính tích vô hướng và góc giữa hai vectơ $\vec{u} = (0; - 5), \vec{v} = (\sqrt{3}; 1)$ ...

HĐ 4 trang 68 Toán 10 tập 1: Cho ba vectơ $\vec{u} = (x_{1}; y_{1}),$ $\vec{v} = (x_{2}; y_{2}),$ $\vec{w} = (x_{3}; y_{3}) .$ ...

Luyện tập 4 trang 70 Toán 10 tập 1: Cho tam giác ABC với A(‒1;2), B(8;‒1), C(8;8)...

Vận dụng trang 70 Toán 10 tập 1: Một lực $\vec{F}$ không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng...

Bài 4.21 trang 70 Toán 10 tập 1: Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ...

Bài 4.22 trang 70 Toán 10 tập 1: Tìm điều kiện của $\vec{u}, \vec{v}$ để...

Bài 4.23 trang 70 Toán 10 tập 1: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 2), B(‒4; 3)...

Bài 4.24 trang 70 Toán 10 tập 1: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(‒4; 1), B(2; 4), C(2; ‒2)...

Bài 4.25 trang 70 Toán 10 tập 1: Chứng minh rằng với mọi tam giác ABC...

Bài 4.26 trang 70 Toán 10 tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M...

Bài viết liên quan

189 lượt xem

« Trang trước

Trang sau »

Có thể bạn quan tâm

Giải sbt Địa lí 10 – Chân trời sáng tạo

Giải sgk Địa lí 10 – Chân trời sáng tạo

Giải sbt Địa lí 10 – Cánh Diều

Giải sgk Địa lí 10 – Cánh Diều

Giải sbt Địa lí 10 – Kết nối tri thức

Giải sgk Địa lí 10 – Kết nối tri thức

Giải sbt Lịch sử 10 – Chân trời sáng tạo

Giải sgk Lịch sử 10 – Chân trời sáng tạo

Giải sbt Lịch sử 10 – Cánh Diều

Giải sgk Lịch sử 10 – Cánh Diều

Giải sbt Lịch sử 10 – Kết nối tri thức

Giải sgk Lịch sử 10 – Kết nối tri thức

Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo

Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo

Giải sbt Giáo dục Kinh tế và Pháp luật 10 - Cánh diều