Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b). Có bao nhiêu tích nhận được
Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton
Hoạt động 2 trang 72 Toán 10 Tập 2: Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b).
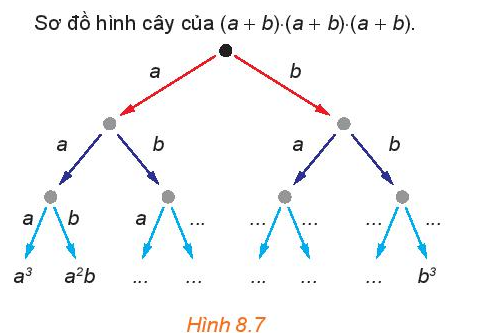
Có bao nhiêu tích nhận được lần lượt bằng a3, a2b, ab2, b3?
Hãy so sánh chúng với các hệ số nhận được khi khai triển (a + b)3.
Lời giải
Theo quy tắc xây dựng sơ đồ hình cây như HĐ1, ta điền được các biểu thức trong sơ đồ hình cây của tích (a + b) . (a + b) . (a + b) như hình sau:
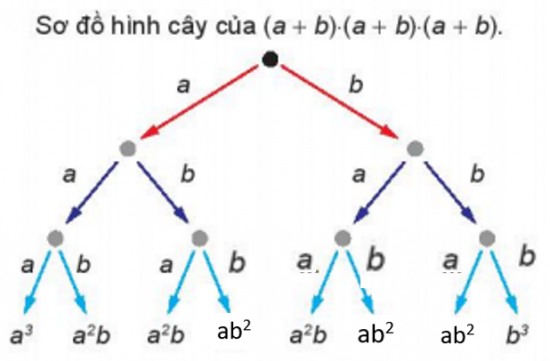
Từ đó, ta có:
- có 1 đơn thức bằng a3;
- có 3 đơn thức bằng a2b;
- có 3 đơn thức bằng ab2;
- có 1 đơn thức bằng b3.
Các hệ số nhận được: 1, 3, 3, 1.
Ở lớp 8 ta đã biết, khai triển (a + b)3 = a3 + 3a2b + 3ab2 + b3.
Vậy các hệ số của khai triển trừng với các hệ số của các tích nhận được.
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Mở đầu trang 72 Toán 10 Tập 2: Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển: (a + b)2 = a2 + 2ab + b2; (a + b)3 = a3 + 3a2b + 3ab2 + b3...
Luyện tập 1 trang 73 Toán 10 Tập 2: Khai triển (x – 2)4...
Luyện tập 2 trang 74 Toán 10 Tập 2: Khai triển (3x – 2)5...
Bài 8.13 trang 74 Toán 10 Tập 2: Tìm hệ số của x^4 trong khai triển của (3x –1)5...
Bài viết liên quan
- Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển: (a + b)^2 = a^2 + 2ab + b^2; (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
- Sơ đồ hình cây của tích hai nhị thức (a + b) . (c + d) được xây dựng như sau: Từ một điểm gốc, kẻ các mũi tên
- Sơ đồ hình cây của khai triển (a + b)^4 được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 2^4
- Khai triển (x – 2)^4
- Tương tự như HĐ3, sau khi khai triển (a + b)^5, ta thu được một tổng gồm 2^5 đơn thức có dạng x . y . z . t . u
