Lớp 10 Chương 3: Hệ thức lượng trong tam giác

Cho tam giác ABC có trung tuyến AM. Chứng minh rằng

Lời giải Bài 3.16 trang 44 Toán 10 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.
141 lượt xem
« Trang trước
Chia sẻ
Trang sau »

Giải Toán lớp 10 Bài tập cuối chương 3

Bài 3.16 trang 44 Toán 10 tập 1: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a) cosAMB^+cosAMC^=0;

b) MA2 + MB2 – AB2 = 2MA.MB.cosAMB^ và MA2 + MC2 – AC2 = 2MA.MC.cosAMC^;

c) MA2=2AB2+AC2−BC24 (công thức đường trung tuyến).

Lời giải:

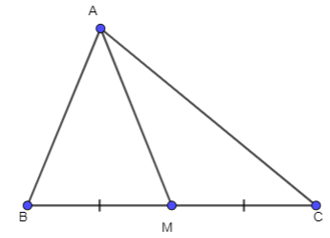
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng (ảnh 1)

a) Ta có: AMB^+AMC^=180o

⇒ AMC^=180o−AMB^

⇒ cosAMB^=−cos180o−AMB^=−cosAMC^

⇒ cosAMB^+cosAMC^=−cosAMC^+cosAMC^=0

Vậy cosAMB^+cosAMC^=0 (đpcm)

b) Áp dụng định lí côsin trong ΔAMB, ta có:

AB2 = MA2 + MB2 – 2MA.MB.cosAMB^ 

⇔ MA2 + MB2 – AB2 = 2MA.MB.cosAMB^ (1)

Áp dụng định lí côsin trong ΔAMC, ta có:

AC2 = MA2 + MC2 – 2MA.MC.cosAMC^

⇔ MA2 + MC2 – AC2 = 2MA.MC.cosAMC^ (2)

Từ (1) và (2) suy ra điều phải chứng minh.

c) Từ (1) suy ra: MA2 = AB2 – MB2 + 2MA.MB.cosAMB^

Từ (2) suy ra: MA2 = AC2 – MC2 + 2MA.MC.cosAMC^

Cộng vế với vế, ta được:

2MA2 = (AB2 – MB2 + 2MA.MB.cosAMB^) + (AC2 – MC2 + 2MA.MC.cosAMC^)

⇔2MA2 = AB2 + AC2 – MB2 – MC2 + 2MA.MB.cosAMB^ + 2MA.MC.cosAMC^

Mà MB=MC=BC2(do AM là trung tuyến) nên:

2MA2 = AB2 + AC2 – BC22 – BC22 + 2MA.MB.cosAMB^ + 2MA.MB.cosAMC^

⇔2MA2 = AB2 + AC2 – 2 . BC22 + 2MA.MB.(cosAMB^ + cosAMC^)

⇔2MA2 = AB2 + AC2 – BC22

⇔ MA2=AB2+AC2−BC222

⇔MA2=2AB2+AC2−BC24 (công thức đường trung tuyến).

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Bài viết liên quan

141 lượt xem
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm