Trên mặt phẳng tọa độ Oxy, hãy vẽ các vectơ OA, MN với A(1;2), M(0;‒1), N(3;5)
Giải Toán lớp 10 Bài 7: Các khái niệm mở đầu
Bài 4.5 trang 50 Toán 10 tập 1: Trên mặt phẳng tọa độ Oxy, hãy vẽ các vectơ với A(1;2), M(0;‒1), N(3;5)
a) Chỉ ra mối quan hệ giữa hai vectơ trên.
b) Một vật thể khởi hành từ M và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vectơ . Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu vật sẽ tới N?
Lời giải
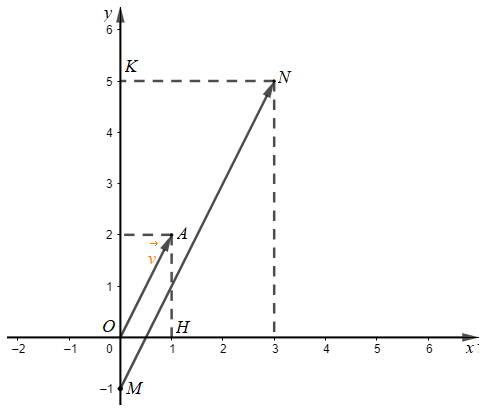
a) Dựng các điểm B(0; 2) và K(0; 5).
Khi đó OB = 2, BA = 1, MK = 6, KN = 3.
Suy ra hai tam giác OAB và MNK là các tam giác vuông đồng dạng.
Do đó .
Suy ra OA // MN và .
Như vậy, hai vectơ và là hai vectơ cùng hướng và vectơ có độ dài gấp 3 lần độ dài của vectơ .
b) Vì và là hai vectơ cùng hướng nên khi vật thể khởi hành từ M và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi thì vật thể đó sẽ đi qua điểm N.
Hơn nữa, sau mỗi giờ vật đó đi được quãng đường bằng và .
Vậy nếu coi độ lớn của OA là một đơn vị giờ thì sau khi khởi hành 3 giờ vật sẽ tới N.
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Luyện tập 1 trang 47 Toán 10 tập 1: Cho tam giác đều ABC với cạnh có độ dài bằng a...
HĐ 3 trang 48 Toán 10 tập 1: Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ...
Luyện tập 2 trang 49 Toán 10 tập 1: Cho hình thang cân ABCD với hai đáy AB, CD,AB < CD...
Bài 4.1 trang 50 Toán 10 tập 1: Cho ba vectơ đều khác . Những khẳng định nào sau...
Bài 4.2 trang 50 Toán 10 tập 1: Trong Hình 4.12, hãy chỉ ra các vectơ cùng phương...
Bài 4.3 trang 50 Toán 10 tập 1: Chứng minh rằng tứ giác ABCD là một hình bình hành...
Bài 4.4 trang 50 Toán 10 tập 1: Cho hình vuông ABCD có hai đường chéo cắt nhau tại O...
Bài 4.5 trang 50 Toán 10 tập 1: Trên mặt phẳng tọa độ Oxy, hãy vẽ các vectơ...
Bài viết liên quan
- Giải Toán 10 Kết nối tri thức Bài 8: Tổng và hiệu của hai vectơ
- Giải Toán 10 Kết nối tri thức Bài 9: Tích của một vecto với một số
- Giải Toán 10 Kết nối tri thức Bài 10: Vectơ trong mặt phẳng tọa độ
- Giải Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vecto
- Giải Toán 10 Kết nối tri thức Bài tập cuối chương 4
