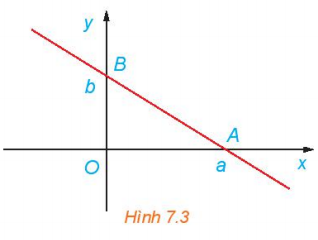
(Phương trình đoạn chắn của đường thẳng) Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab khác 0
Lời giải Bài 7.5 trang 34 Toán 10 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải Toán 10 Kết nối tri thức Bài 19: Phương trình đường thẳng
Bài 7.5 trang 34 Toán 10 Tập 2:
(Phương trình đoạn chắn của đường thẳng)
Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H7.3) có phương trình là:
Lời giải
Ta có: = (-a; b)
Đường thẳng AB nhận = (-a; b) làm vectơ chỉ phương, do đó vectơ pháp tuyến là: (b; a)
Vậy phương trình tổng quát của đường thẳng AB đi qua điểm A (a; 0) và có vectơ pháp tuyến (b; a) là: b(x – a) + a(y – 0) = 0
⇔ bx + ay – ab = 0 (1)
Vì ab ≠ 0 nên chia cả 2 vế của (1) cho tích ab ta được: hay .
Vậy phương trình đường thẳng AB là: .
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Bài viết liên quan
- Giải Toán 10 Kết nối tri thức Bài 19: Phương trình đường thẳng
- Giải Toán 10 Kết nối tri thức Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
- Giải Toán 10 Kết nối tri thức Bài 21: Đường tròn trong mặt phẳng tọa độ
- Giải Toán 10 Kết nối tri thức Bài 22: Ba đường Conic
- Giải Toán 10 Kết nối tri thức Bài tập cuối chương 7
