Cho hàm số bậc hai y = f(x) = x^2 – 4x + 3. a) Xác định hệ số a. Tính f(0), f(1), f(2), f(3), f(4) và nhận xét
Giải Toán 10 Kết nối tri thức Bài 17: Dấu của tam thức bậc hai
Hoạt động 2 trang 19 Toán 10 Tập 2: Cho hàm số bậc hai y = f(x) = x2 – 4x + 3.
a) Xác định hệ số a. Tính f(0), f(1), f(2), f(3), f(4) và nhận xét về dấu của chúng so với dấu của hệ số a.
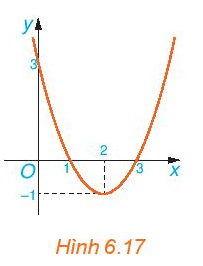
b) Cho đồ thị hàm số y = f(x) (H.6.17). Xét trên từng khoảng (– ∞; 1), (1; 3), (3; +∞), đồ thị nằm phía trên hay nằm phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Lời giải
a) Hàm số bậc hai y = f(x) = x2 – 4x + 3.
Ta có hệ số a = 1 > 0.
f(0) = 02 – 4 . 0 + 3 = 3 > 0, f(0) cùng dấu với hệ số a.
f(1) = 12 – 4 . 1 + 3 = 0, f(1) không mang dấu.
f(2) = 22 – 4 . 2 + 3 = – 1 < 0, f(2) trái dấu với hệ số a.
f(3) = 32 – 4 . 3 + 3 = 0, f(3) không mang dấu.
f(4) = 42 – 4 . 4 + 3 = 3 > 0, f(4) cùng dấu với hệ số a.
b) Từ đồ thị H.6.17, ta có:
- Trên các khoảng (– ∞; 1) và (3; +∞), đồ thị hàm số nằm phía trên trục Ox.
- Trên khoảng (1; 3), đồ thị hàm số nằm phía dưới trục Ox.
c) Khi đồ thị hàm số nằm trên trục Ox thì f(x) > 0 và khi đồ thị hàm số nằm phía dưới trục Ox thì f(x) < 0.
Lại có hệ số a = 1 > 0.
Do đó, trên các khoảng (– ∞; 1) và (3; +∞), f(x) cùng dấu với hệ số a; trên khoảng (1; 3), f(x) trái dấu với hệ số a.
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
