Giải Toán 10 Kết nối tri thức Bài tập cuối năm

Bài 9 trang 96 Toán 10 Tập 2: Cho hàm số y = f(x) = ax² + bx + c với đồ thị là parabol (P) có đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$ và đi qua điểm A(1; 2).

a) Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x – h)² + k, trong đó I(h; k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.

b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

c) Giải bất phương trình f(x) ≥ 0.

Lời giải

a)

• Theo bài ra ta có parabol có đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$ nên h = $\frac{5}{2}$ và k = $-\frac{1}{4}$.

Do đó, phương trình của parabol (P) có dạng: $y=a{\left(x-\frac{5}{2}\right)}^2-\frac{1}{4}$.

Lại có parabol (P) đi qua điểm A(1; 2) nên thay tọa độ điểm A vào phương trình parabol ta được: $2=a{\left(1-\frac{5}{2}\right)}^2-\frac{1}{4}$. Suy ra a = 1.

Vậy parabol (P) có phương trình là $y=1.{\left(x-\frac{5}{2}\right)}^2-\frac{1}{4}$ hay y = x² – 5x + 6.

• Vẽ parabol (P).

- Hệ số a = 1 > 0 nên parabol có bề lõm hướng lên trên.

Parabol (P) có

- Đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$;

- Phương trình trục đối xứng $x=\frac{5}{2}$;

- Giao điểm của (P) với trục tung là điểm B(0; 6);

- Phương trình x² – 5x + 6 = 0 có hai nghiệm x = 2 và x = 3. Do đó, giao điểm của (P) với trục hoành là C(2; 0) và D(3; 0).

Vẽ đường cong đi qua các điểm trên ta được parabol (P).

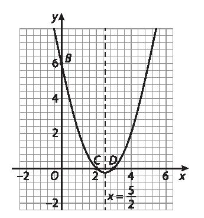
b) Từ hình vẽ ở câu a, ta thấy hàm số y = x² – 5x + 6 đồng biến trên khoảng $\left(\frac{5}{2};+\infty \right)$ và nghịch biến trên khoảng $\left(-\infty ;\frac{5}{2}\right)$.

c) f(x) ≥ 0

⇔ x² – 5x + 6 ≥ 0

Tam thức bậc hai f(x) = x² – 5x + 6 có hệ số a = 1 > 0 và có hai nghiệm phân biệt x₁ = 2 và x₂ = 3, do đó f(x) ≥ 0 ⇔ x ≤ 2 hoặc x ≥ 3.

Vậy tập nghiệm của bất phương trình là S = (– ∞; 2] ∪ [3; + ∞).

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: