Thi Online (2023) Đề thi thử Toán THPT Chuyên Hạ Long có đáp án
Thi Online (2023) Đề thi thử Toán THPT Chuyên Hạ Long có đáp án
-
1094 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn D
Phương trình mặt cầu (S) có tâm I(-1;0;2) và bán kính R = 3 làCâu 2:
 Xem đáp án
Xem đáp án
Chọn D
Số cách xếp 5 người đứng thành một hàng ngang là 5! = 120 cách.
Câu 3:
Cho hàm số y = f(x) có đạo hàm f'(x) trên R và có bảng biến thiên dưới đây.
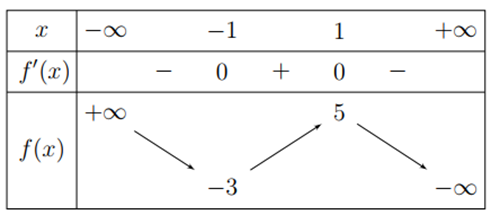
Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Chọn D
Khẳng định đúng là: Điểm cực đại của đồ thị hàm số là (1;5)Câu 4:
 Xem đáp án
Xem đáp án
Chọn A
Diện tích xung quanh Sxq của khối nón được tính theo công thứcCâu 5:
 Xem đáp án
Xem đáp án
Chọn D
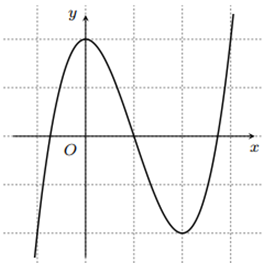
Ta thấy đồ thị dạng hàm số bậc ba với a > 0. Đồ thị đi qua điểm có tọa độ (1;0).
Suy ra hàm số có đồ thị là đường cong như hình.
Câu 6:
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên dưới đây. Hàm số đồng biến trên khoảng nào dưới đây?
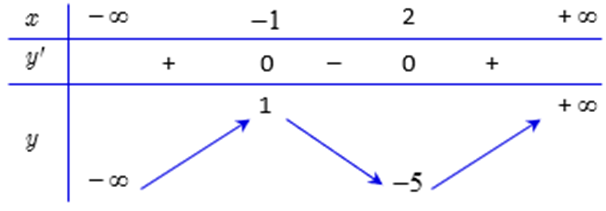
 Xem đáp án
Xem đáp án
Chọn A
Hàm số đồng biến trên khoảng và .
Suy ra hàm số đồng biến trên khoảngCâu 7:
 Xem đáp án
Xem đáp án
Chọn D
Phương trình hoành độ giao điểm
.
Suy ra a + b = 2Câu 8:
 Xem đáp án
Xem đáp án
Chọn B
Điều kiện: x - 2022 > 0 <=> x > 2022.
Tập xác đinh:Câu 11:
 Xem đáp án
Xem đáp án
Chọn B
Thể tích V khối chóp có diện tích đáy B và chiều cao h làCâu 14:
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên như sau
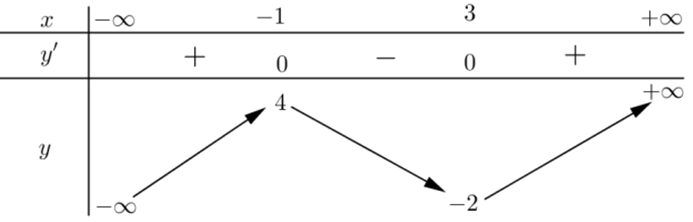
Hỏi phương trình f(x) = 3 có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Chọn C
Vẽ đường thẳng y = 3 lên bảng biến thiên của hàm số y = f(x).
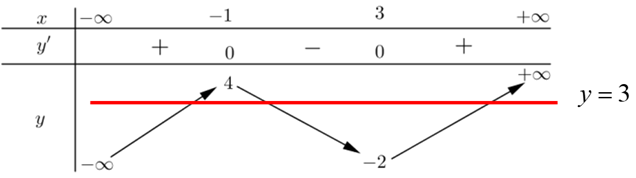
Suy ra phương trình f(x) = 3 có 3 nghiệm phân biệt.
Câu 17:
 Xem đáp án
Xem đáp án
Chọn A
Tập xác định
Ta có
Suy ra đường tiệm cận đứng của đồ thị hàm số là đường thẳng x = 3Câu 18:
 Xem đáp án
Xem đáp án
Chọn B
Theo tính chất của phép toán nguyên hàm.Câu 19:
 Xem đáp án
Xem đáp án
Chọn C
Mặt cầu tâm I đường kính AB nên suy ra I là trung điểm AB
Suy raCâu 21:
 Xem đáp án
Xem đáp án
Chọn D
Câu 22:
 Xem đáp án
Xem đáp án
Chọn D
. Suy ra hàm số y đồng biến trên [-2;2]
Suy raCâu 23:
Giá dầu thô WTI hôm nay (ngày 6/1/2023) là 81 USD. Giả sử ngày mai (ngày 7/1/2023) giảm 10% và ngày kia (ngày 8/1/2023) tăng 10%. Hỏi giá dầu thô WTI ngày 8/1/2023 là bao nhiêu USD?
 Xem đáp án
Xem đáp án
Chọn D
Giá dầu ngày ngày 7/1/2023 là: USD.
Giá dầu ngày ngày 8/1/2023 là: USD.Câu 24:
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của không gian mẫu là .
Gọi A là biến cố để 2 học sinh được chọn cùng giới tính.
+) Số cách chọn hai học sinh nam là
+) Số cách chọn hai học sinh nữ là
Từ đó suy ra
Xác xuất của biến cố A làCâu 25:
 Xem đáp án
Xem đáp án
Chọn A
Câu 26:
 Xem đáp án
Xem đáp án
Chọn A
Câu 27:
Cho khối trụ có bán kính đường tròn đáy r = a và thể tích Diện tích xung quanh của khối trụ đã cho bằng
 Xem đáp án
Xem đáp án
Chọn D
Ta có: .
Suy raCâu 29:
 Xem đáp án
Xem đáp án
Chọn B
Ta có: với h chính là đường cao của tam giác SAB.
Do đó,Câu 30:
 Xem đáp án
Xem đáp án
Chọn A
Ta có:Câu 31:
 Xem đáp án
Xem đáp án
Chọn A
Câu 32:
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên dưới đây
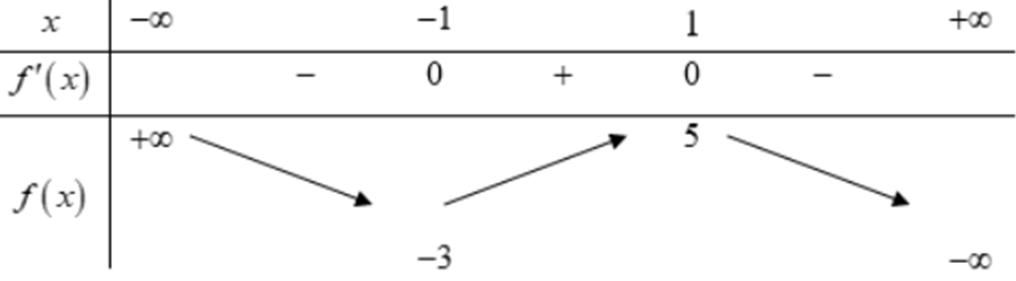
 Xem đáp án
Xem đáp án
Chọn B
Dựa vào bảng biến thiên, phương trình f(x) = m có ba nghiệm phân biệt <=> -3 < m < 5Câu 34:
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
VậyCâu 36:
 Xem đáp án
Xem đáp án
Chọn C
A, B, C lần lượt là hình chiếu vuông góc của M lên các mặt phẳng nên tọa độ của chúng là: .
Do đó,Câu 37:
 Xem đáp án
Xem đáp án
Chọn C
Tập xác định :
nên y = 0 là tiệm cận ngang của đồ thị hàm số
nên x = 2 là tiệm cận đứng của đồ thị hàm số
Vậy đồ thị hàm số có 2 đường tiệm cận.Câu 38:
 Xem đáp án
Xem đáp án
Chọn A
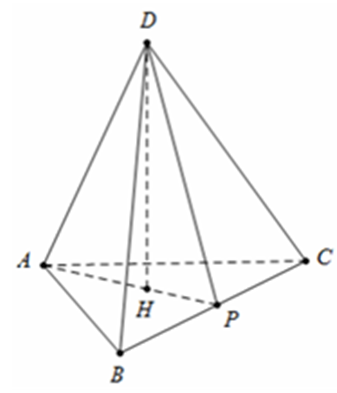
Xét tứ diện đều ABCD cạnh AB = x, P là trung điểm BC, đường cao . Áp dụng định lí Pi-ta-go trong tam giác ![]() ADH ta có: .
ADH ta có: .
Do đó:
Vậy .Câu 40:
 Xem đáp án
Xem đáp án
Chọn D
Đặt . Do . Áp dụng BĐT Co-si cho 2 số dương
Ta có: .
Dấu ''='' xảy ra . Vậy GTNN của P bằng 3 khi .
Câu 41:
 Xem đáp án
Xem đáp án
Chọn B
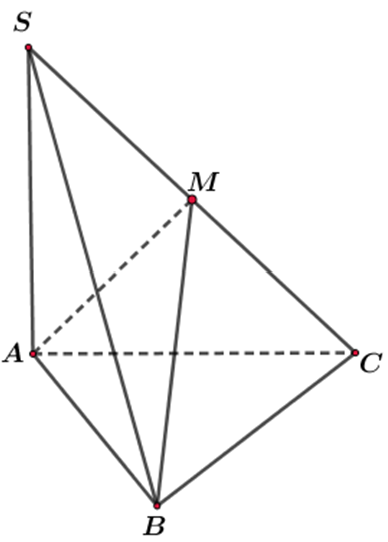
Vì M là trung điểm của SC nên
Câu 42:
 Xem đáp án
Xem đáp án
Chọn C
Gọi I là trung điểm AB => I(3;5;4)
Khi đó , với H(3;5;0) là hình chiếu của I lên mặt phẳng (Oxy)
Dấu “ = ” xảy ra khiCâu 43:
Một viên đá hình trụ đặc có bán kính đáy bằng 2cm, chiều cao bằng 4cm được đặt vừa khít vào trong một chiếc ly rỗng có phần chứa nước là một hình nón như hình vẽ. Biết rằng chiều cao của phần chứa nước của ly gấp đôi chiều cao viên đá, miệng ly bằng bề mặt viên đá. Tính thể tích nước (ml) cần đổ vào ly cho đầy, làm tròn đến 2 chữ số thập phân sau dấu phẩy, biết do lực đẩy Archimedes, khi đổ nước vào, có 8% thể tích viên đá nổi lên phía trên mặt nước.
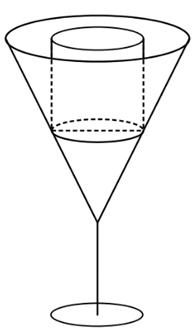
 Xem đáp án
Xem đáp án
Chọn D
Gọi lần lượt là bán kính đáy của phần chứa nước và viên đá, ta có .
Gọi lần lượt là chiều cao của phần chứa nước và viên đá, ta có .
Thể tích nước cần đổ vào ly cho đầy là (ml)Câu 44:
 Xem đáp án
Xem đáp án
Chọn B
Hàm số y = f(x) có 4 điểm cực trị khi và chỉ khi phương trình f'(x) = 0 có 4 nghiệm phân biệt. Nói cách khác, phương trình có 2 nghiệm phân biệt khác 0 và -1.
.
Có giá trị nguyên của m thuộc [-10;10] thỏa yêu cầu bài toán làCâu 45:
 Xem đáp án
Xem đáp án
Chọn B
. Điều kiện của phương trình x > 0
+ có nghiệm duy nhất x = 3 vì hàm số đồng biến, hàm số nghịch biến.
+ .
Đặt .
Vậy phương trình (3) có không quá 2 nghiệm. Phương trình (3) có 2 nghiệm x = 1, x = 3.
Vậy tổng các nghiệm là 1 + 3 = 4Câu 46:
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện
Đặt . Vì .
Ta được phương trình . Bài toán đưa về tìm số các số nguyên dương a không vượt quá 10 để phương trình có 1 nghiệm duy nhất .
Vì mỗi t (0 < t < 3) thì phương trình có 2 giá trị phân biệt của x
Đặt
.
Bảng biến thiên
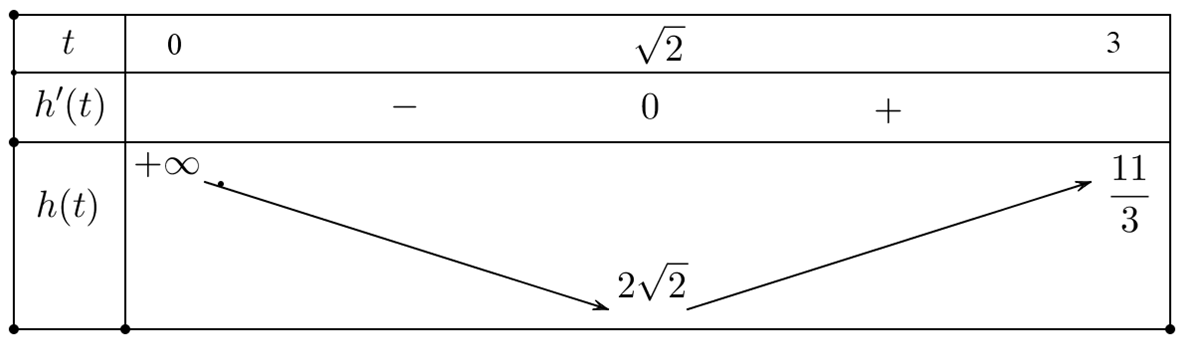
Câu 47:
 Xem đáp án
Xem đáp án
Chọn A
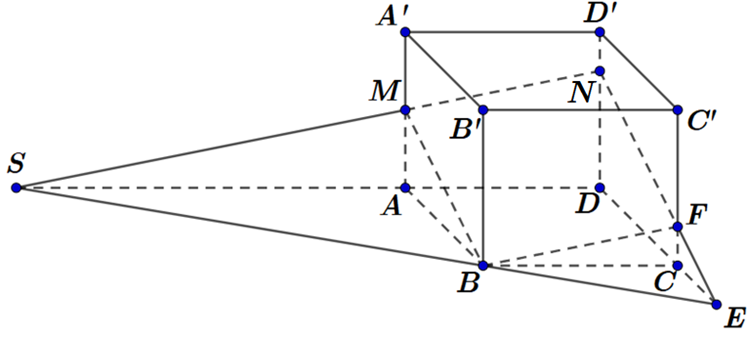
Gọi , và .
Ta có và .
Ta có
.
MàCâu 48:
 Xem đáp án
Xem đáp án
Chọn D
Câu 49:
 Xem đáp án
Xem đáp án
Chọn D
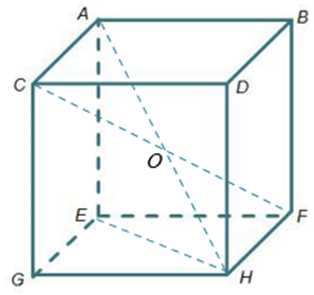
Vì là lăng trụ tứ giác đều nên ta có: AH = DE = CF = BF: là các đường chéo của lăng trụ tứ giác đều.
Do vậy tâm O của khối cầu ngoại tiếp lăng trụ tứ giác đều là giao điểm của 4 đường chéo AH, DE, CF, BF.
Ta có .
Suy ra bán kính mặt cầu ngoại tiếp lăng trụ tứ giác đều làCâu 50:
 Xem đáp án
Xem đáp án
Chọn A
Đặt . Ta có BBT của hàm số :
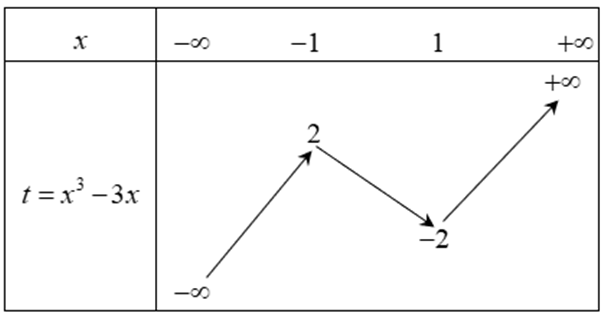
Khi đó ta có:
Để phương trình (1) có 7 nghiệm phân biệt thì phương trình (2) có 3 nghiệm t trong đó có 2 nghiệm và 1 nghiệm t > 2 hoặc t < -2.
Ta có BBT của hàm số :