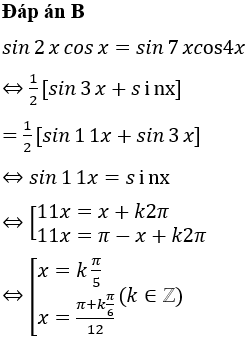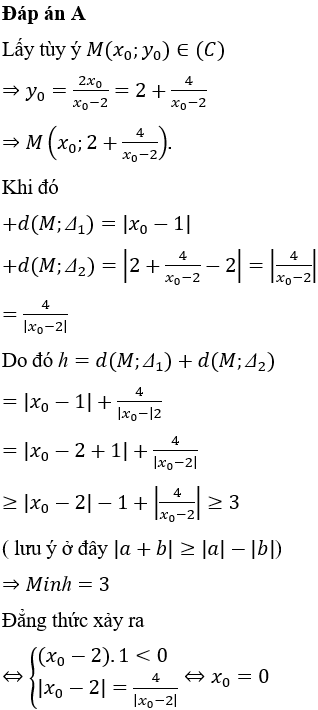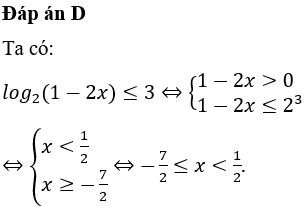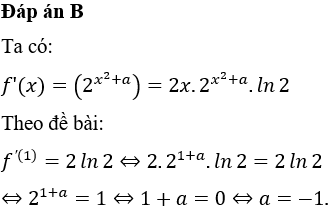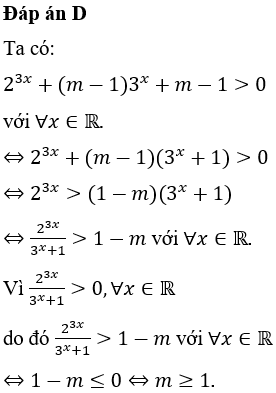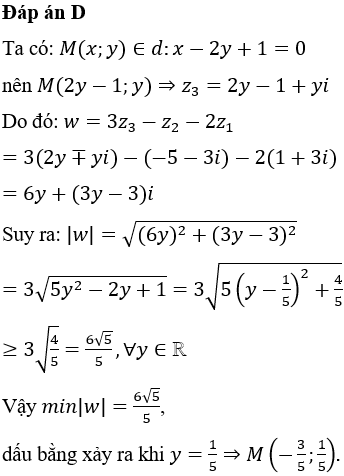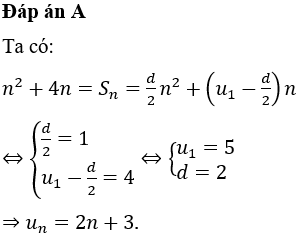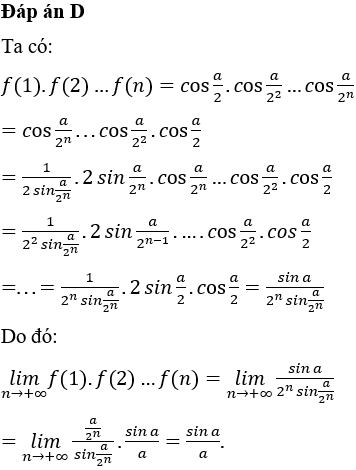Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết - đề 1
-
6032 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 3:
Từ các chữ số 1, 2, 3, 4 ta có thể tạo thành bao nhiêu số tự nhiên gồm 6 chữ số, trong đó chữ số 1 xuất hiện đúng 3 lần, ba chữ số 2, 3, 4 hiện diện đúng 1 lần.
 Xem đáp án
Xem đáp án
Đáp án A
Thêm vào hai chữ số 1 vào tập hợp các chữ số đã cho ta được tập E = {1,1,1,2,3,4}
Xem các số 1 là khác nhau thì mỗi hoán vị của 6 phần tử của E cho ta một số có 6 chữ số thỏa mãn bài toán. Như vậy ta có 6! số. Tuy nhiên khi hoán vị vủa ba số 1 cho nhau thì giá trị con số không thay đổi nên mỗi số như vậy ta đếm chúng đến 3! lần.
Vậy số các số thỏa mãn yêu cầu bài toán là .
Chú ý: Ta có thể giải như sau, ta gọi số 6 chữ số cần tìm là , chọn 3 vị trí trong 6 vị trí để đặt ba chữ số 1 có cách, xếp 3 chữ số 2, 3, 4 vào ba vị trí còn lại có 3! cách do đó
Câu 9:
Cho a, b là hai số thực dương. Tìm số điểm cực trị của hàm số
 Xem đáp án
Xem đáp án
Đáp án D
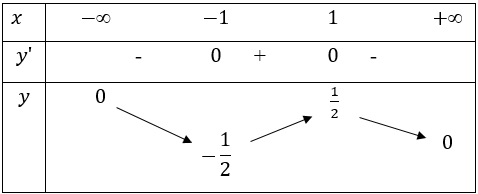
Đặt ta thấy nên điểm cực đại ở dưới trục hoành và có ba nghiệm phân biệt g(x) sẽ có đồ thị như đồ thị hình bên.
Đồ thị của hàm số là phần nằm phía dưới trục hoành và hai nhánh phía trên trục hoành.
Đồ thị của hàm số có được bằng cách lấy phần phía dưới trục hoành đối xứng qua trục hoành kết hợp với phần ở trên trục hoành. Đó chính là tất cả phần đồ thị trên trục hoành.
Dựa vào đồ thị => Hàm số có 5 cực trị.
Câu 12:
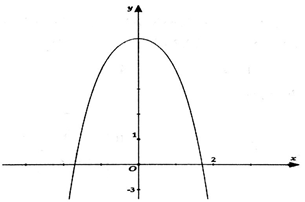
Đồ thị hình bên là đồ thị của một trong 4 đồ thị của các hàm số ở các phương án A, B, C, D dưới đây. Hãy chọn phương án đúng.
 Xem đáp án
Xem đáp án
Đáp án B
Ta thấy đồ thị hàm số chỉ có một điểm cực trị nên loại đáp án D.
Từ trái sang phải, đồ thị hàm số đi từ dưới lên, do đó hệ số của phải âm. Suy ra loại được đáp án A.
Với thì y < 0. Thay vào hai đáp án B, C ta thấy đáp án B thỏa mãn còn đáp án C không thỏa mãn.
Câu 24:
Cho tứ diện ABCD có , đáy ABC thỏa mãn điều kiện = Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC. Tính thể tích V của khối cầu ngoại tiếp khối chóp A.BCHK
 Xem đáp án
Xem đáp án
Đáp án A
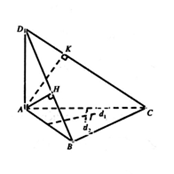
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Do tam giác AHB vuông tại H nên I thuộc trục của tam giác AHB. Tương tự I cũng thuộc trục của tam giác AKC. Suy ra I cách đều A, B, H,K, C nên nó là tâm mặt cầu ngoại tiếp hình chóp A.BCKH.
Gọi R là bán kính mặt cầu ngoại tiếp hình chóp A.BCKH thì R cũng là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có:
cot A + cot B + cot C
Nên
Câu 25:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hình vuông ABCD và A'B'C'D'. Tính S.
 Xem đáp án
Xem đáp án
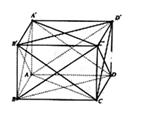
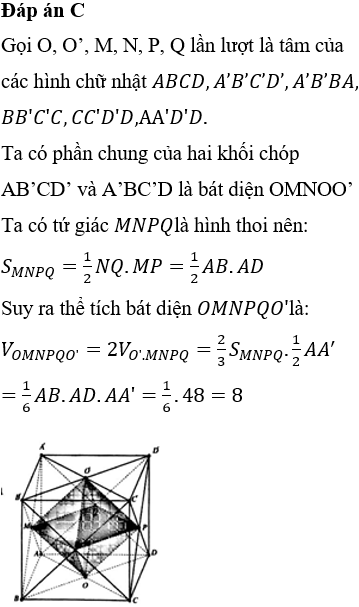
Đáp án C
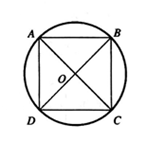
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông ABCD;
Do đó thể tích hình trụ cần tìm bằng
Câu 26:
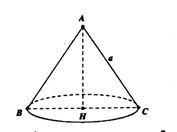
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh của hình nón đó.
 Xem đáp án
Xem đáp án
Đáp án B
Khi quay tam giác ABC quanh đường cao AH ta được hình nón có bán kính đường tròn đáy là R = BH = , đường sinh l = AB = a.
Vậy diện tích xung quanh là
Câu 30:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y - 3z + 5 = 0. Véc tơ nào sau đây là véc tơ pháp tuyến của mặt phẳng (P)?
 Xem đáp án
Xem đáp án
Đáp án D
Từ phương trình tổng quát của mặt phẳng (P) suy ra véc tơ pháp tuyến của mặt phẳng (P) là .
Câu 49:
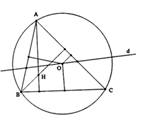
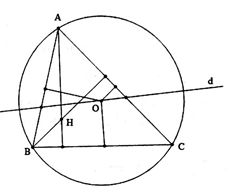
Cho tam giác ABC nội tiếp đường tròn (O). Qua O kẻ đường thẳng d. Quy tắc nào sau đây là một phép biến hình:
 Xem đáp án
Xem đáp án
Đáp án D
Các quy tắc A, B, C đều biến O thành nhiều hơn một điểm nên đó không phải là phép biến hình. Quy tắc D biến O thành điểm H duy nhất nên đó là phép biến hình.