Các dạng bài tập về hàm số và cách giải - Toán lớp 9

I. Lý thuyết

1. Khái niệm hàm số

- Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho mỗi giá trị của x, ta luôn xác định được chỉ một giá trị của y thì y được gọi là hàm số của x, x là biến số. Ta viết:

y = f(x); y = g(x)…

Ví dụ: y = 2x + 4; y = -3x + 5 là hàm số của y theo x.

Chú ý: Khi x thay đổi mà y không thay đổi thì hàm số y = f(x) là hàm hằng.

2. Điều kiện xác định của hàm số

Điều kiện xác định của hàm số y = f(x) là tất cả các giá trị của x sao cho f(x) có nghĩa.

3. Giá trị của hàm số

Giá trị của hàm số f(x) tại điểm $x_0$ là $y_0=f\left(x_0\right)$ .

4. Đồ thị hàm số

Đồ thị hàm số y = f(x) là tập hợp tất cả các điểm M(x; y) trong mặt phẳng tọa độ Oxy sao cho x, y thỏa mãn y = f(x).

5. Hàm số đồng biến, hàm số nghịch biến

Cho hàm số y = f(x) có tập xác định là $ℝ$ .

- Nếu giá trị của biến x tăng lên mà giá trị y = f(x) tương ứng cũng tăng thì hàm số y = f(x) là hàm số đồng biến trên $ℝ$ .

- Nếu giá trị của biến x tăng lên mà giá trị của y = f(x) tương ứng giảm thì hàm số y = f(x) là hàm số nghịch biến trên $ℝ$ .

- Nếu $x_1<x_2$ và $f\left(x_1\right)<f\left(x_2\right)$  thì hàm số y = f(x) đồng biến trên $ℝ$ .

- Nếu $x_1<x_2$ và $f\left(x_1\right)>f\left(x_2\right)$  thì hàm số y = f(x) nghịch biến trên $ℝ$ .

Để xét tính đồng biến nghịch biến của hàm số ta xét dấu của T, với $T=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$  và $x_1,x_2\in ℝ$

Nếu T < 0 thì hàm số nghịch biến trên $ℝ$ .

Nếu T > 0 thì hàm số đồng biến trên $ℝ$ .

II. Các dạng bài và phương pháp giải

Dạng 1: Tìm điều kiện xác định của hàm số

Phương pháp giải: Chú ý đến một số biểu thức có điều kiện đặc biệt như căn, phân thức.

 Hàm số dạng căn thức $y=\sqrt{P\left(x\right)}$ có nghĩa khi $P\left(x\right)\ge 0$

Hàm số dạng phân thức $y=\frac{A\left(x\right)}{B\left(x\right)}$  có nghĩa khi $B\left(x\right)\ne 0$

Hàm số dạng phân thức $y=\frac{A\left(x\right)}{\sqrt{B\left(x\right)}}$ có nghĩa khi $B\left(x\right)>0$ .

Ví dụ: Tìm điều kiện xác định của các hàm số sau

a) $y=\frac{2x-1}{3x-5}$

b) $y=\sqrt{2x+1}+\frac{1}{x+2}$

c) $y=\frac{1+\sqrt{3-x}}{x+3}$

Lời giải:

a) Hàm số $y=\frac{2x-1}{3x-5}$ xác định khi và chỉ khi

$3x-5\ne 0$

$\iff 3x\ne 5$

$\iff x\ne 5:3$

$\iff x\ne \frac{5}{3}$

Vậy điều kiện xác định của hàm số là $x\ne \frac{5}{3}$ .

b) Hàm số $y=\sqrt{2x+1}+\frac{1}{x+2}$ xác định khi và chỉ khi

$\left\{\begin{array}{l}2x+1\ge 0\\ x+2\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}2x\ge -1\\ x\ne -2\end{array}\right.$

$\iff \left\{\begin{array}{l}x\ge -1:2\\ x\ne -2\end{array}\right.$

$\iff \left\{\begin{array}{l}x\ge \frac{-1}{2}\\ x\ne -2\end{array}\right.$

$\Rightarrow x\ge \frac{-1}{2}$

Vậy điều kiện xác định của hàm số là $x\ge \frac{-1}{2}$ .

c) Hàm số $y=\frac{1+\sqrt{3-x}}{x+3}$ xác định khi và chỉ khi:

$\left\{\begin{array}{l}3-x\ge 0\\ x+3\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}-x\ge -3\\ x\ne -3\end{array}\right.$

$\iff \left\{\begin{array}{l}x\le 3\\ x\ne -3\end{array}\right.$

Vậy điều kiện xác định của hàm số là  $x\le 3$ và $x\ne -3$

Dạng 2: Tính giá trị hàm số tại một điểm

Phương pháp giải: Để tính giá trị hàm số y = f(x) tại điểm $x_0$  ta thay x = $x_0$ vào y = f(x) được $y_0$  = $f\left(x_0\right)$

Ví dụ 1: Tính giá trị hàm số

a) y = f(x) = $x^3+3x-2$  tại $x_0$ =1.

b) y = f(x) = $\sqrt{3x+1}$ tại $x_0$=2 .

Lời giải:

a) y = f(x) =$x^3+3x-2$

Thay x = $x_0$ = 1 vào hàm số ta được:

$f\left(1\right)=1^3+3.1-2$= 1 + 3 – 2 = 2

Vậy với $x_0$  = 1 thì giá trị hàm số là 2.

b) y = f(x) =$\sqrt{3x+1}$

Thay x = $x_0=2$ vào hàm số ta được:

$f\left(2\right)=\sqrt{3.2+1}=\sqrt{7}$

Vậy với $x_0=2$  thì giá trị hàm số là $\sqrt{7}$ .

Ví dụ 2: Tìm m để hàm số y = f(x) =$3\sqrt{x+1}+m{x}^2-2x+3$ có f(3) = f(-1) với m là tham số.

Lời giải:

Thay x = 3 ta có:

$f\left(3\right)=3\sqrt{3+1}+m{.3}^2-2.3+3$

$f\left(3\right)=6+9m-6+3$

$f\left(3\right)=9m+3$

Thay x = -1 ta có:

$f\left(-1\right)=3\sqrt{-1+1}+m.{\left(-1\right)}^2-2.\left(-1\right)+3$

$\iff f\left(-1\right)=0+m+2+3$

$\iff f\left(-1\right)=m+5$

Vì f(3) = f(-1) nên ta có:

9m + 3 = m + 5

$\iff$9m – m = 5 – 3

$\iff$8m = 2

$\iff$m = 2 : 8

$\iff$m =$\frac{1}{4}$

Vậy m = $\frac{1}{4}$ thì f(3) = f(-1).

Dạng 3: Biểu diễn tọa độ một điểm trên hệ trục tọa độ Oxy

Phương pháp giải: Biểu diễn điểm $M\left(x_0;y_0\right)$

Bước 1: Xác định $x_0$ sau đó vẽ một đường thẳng song song với Oy đi qua $x_0$

Bước 2: Xác định  $y_0$ sau đó vẽ một đường thẳng song song với Ox đi qua $y_0$

Bước 3: Tọa độ điểm M chính là giao của hai đường thẳng trên.

Ví dụ 1: Biểu diễn các điểm sau trên hệ trục tọa độ:

$A\left(2;3\right)$; $B\left(\frac{1}{2};-2\right)$ ;$C\left(-3;2\right)$

Lời giải:

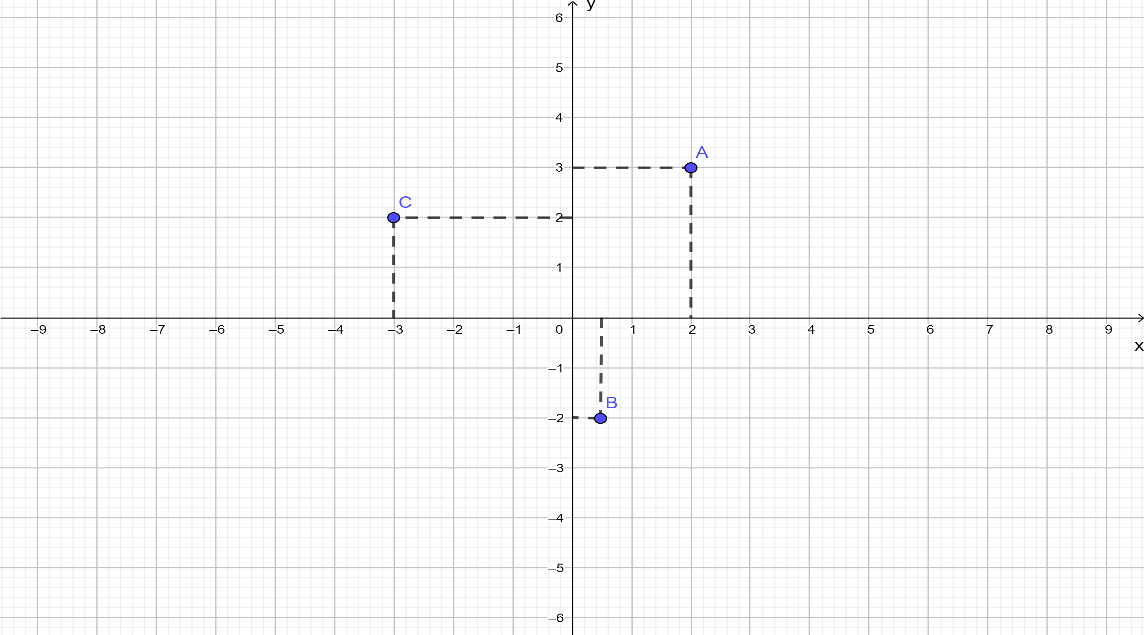
Ví dụ 2: Trong các điểm M(1; -1); N(2; 0), P(-2; 2) điểm nào thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$

Lời giải:

- Xét điểm M(1; -1) có x = 1 và y = -1

Thay x = 1 vào hàm số ta được $y=\frac{1}{2}{.1}^2$$=\frac{1}{2}$$\ne -1$

Vậy M không thuộc đồ thị hàm số

- Xét điểm N(2; 0) có x = 2; y = 0

Thay x = 2 vào hàm số ta được

Vậy điểm N không thuộc đồ thị hàm số

- Xét điểm P(-2; 2) có x = -2; y = 2

Thay x = -2 vào hàm số ta được $y=\frac{1}{2}.{\left(-2\right)}^2=\frac{1}{2}.4=2$

Vậy điểm P thuộc đồ thị hàm số.

Dạng 4: Xét sự đồng biến, nghịch biến của hàm số

Phương pháp giải: Để xét tính đồng biến nghịch biến của hàm số ta xét dấu của T, với $T=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$  và $x_1,x_2\in ℝ$

Nếu T < 0 thì hàm số nghịch biến trên $ℝ$ .

Nếu T > 0 thì hàm số đồng biến trên $\mathit{ℝ}$ .

Ví dụ : Xét tính đồng biến, nghịch biến của hàm số sau

a) y = f(x) = 3x + 1

b) y = f(x) = -6x – 3.

Lời giải:

a) Tập xác định của hàm số là $ℝ$

Với  $x_1,x_2\in ℝ$ ta có:

$f\left(x_1\right)=3x_1+1$

$f\left(x_2\right)=3x_2+1$

Xét $T=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$$=\frac{\left(3x_2+1\right)-\left(3x_1+1\right)}{x_2-x_1}$

$=\frac{3x_2+1-3x_1-1}{x_2-x_1}$$=\frac{3x_2-3x_1}{x_2-x_1}$

$=\frac{3\left(x_2-x_1\right)}{x_2-x_1}=3>0$

Vậy hàm số đã cho đồng biến trên $ℝ$ .

b) Tập xác định của hàm số là $ℝ$

Với $x_1,x_2\in ℝ$ ta có:

$f\left(x_1\right)=-6x_1-3$

$f\left(x_2\right)=-6x_2-3$

Xét $T=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$$=\frac{\left(-6x_2-3\right)-\left(-6x_1-3\right)}{x_2-x_1}$

$=\frac{-6x_2-3+6x_1+3}{x_2-x_1}$$=\frac{-6x_2+6x_1}{x_2-x_1}$

$=\frac{-6\left(x_2-x_1\right)}{x_2-x_1}=-6<0$

Vậy hàm số đã xét nghịch biến trên $ℝ$ .

III. Bài tập tự luyện

Bài 1: Tìm điều kiện xác định của các hàm số sau:

a) $y=3x+1$

b) $y=\frac{3x-2}{\sqrt{x-1}}$

c) $y=\frac{x+2}{3x-3}$

d)$y=\sqrt{4x+1}-2x+\frac{1}{x}$ .

Bài 2: Tính giá trị hàm số

a) $y=\frac{3x+2}{\sqrt{2x+1}}$ tại x = 5

b) $y=\sqrt{4x+1}-6x+\frac{1}{x+3}$ tại x = 0

c) $y=\frac{x^2+2x-1}{3x+3}$ tại x = 5

d) $y=3x^3+2x-5$ tại x = 2.

Bài 3: Tìm m để hàm số sau xác định với mọi x

a) $y=\sqrt{m+1}x+3$

b)  $y=\frac{x^2-3x-1}{mx+5}$ .

Bài 4: Cho các điểm M(-1; 2); N(0; -3); P(4; 2)

a) Biểu diễn các điểm trên cùng một hệ trục tọa độ.

b) Trong các điểm đã cho, điểm nào thuộc hàm số $y=2x^2+\frac{1}{2}x-3$ .

Bài 5: Trên cùng một mặt phẳng tọa độ cho ta giác ABC, biết A(2; 5); B(-1; 1); C(3; 1).

a) Vẽ tam giác ABC trên hệ trục tọa độ.

b) Tính diện tích tam giác ABC.

Bài 6: Xét tính đồng biến, nghịch biến của các hàm số sau

a) $y=5x-1$

b) $y=\frac{-1}{2}x+3$

c) $y=\frac{2}{3}x+3a$  với a là tham số.

Bài 7: Chứng minh

a) $y=2x-5$ luôn đồng biến trên $ℝ$ .

b) $y=\frac{2x+1}{-3}$  luôn nghịch biến trên $\mathit{ℝ}$.

c) $y=\sqrt{a^2+1}.x+3-a$ luôn đồng biến trên $ℝ$ .

Bài 8: Tìm m để hàm số $y=f\left(x\right)=\sqrt{x-1}+mx+2$  (với m là tham số) thỏa mãn $f\left(5-2\sqrt{3}\right)=f\left(2\right)$ .

Bài 9: Cho tứ giác ABCD có A(-1; 2); B(-3; 0); C(2; 0); D(2; 2)

a) Vẽ tứ giác ABCD trên hệ trục tọa độ

b) Coi độ dài mỗi đơn vị trên các trục Ox; Oy là 1cm. Tính diện tích tứ giác ABCD.

Bài 10: Tìm m để hàm số $y=f\left(x\right)=\left(\sqrt{m^2+4}-m\right)x^2-2mx+5$ (với m là tham số) thỏa mãn f(0) = f(1).