Góc ở tâm, số đo cung, liên hệ giữa cung và dây và cách giải - Toán lớp 9

I. Lý thuyết

1. Góc ở tâm

- Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

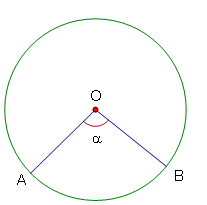
Cho đường tròn (O) hai điểm A, B nằm trên đường tròn. Khi đó $\widehat{AOB}$  là góc ở tâm.

- Nếu $0°<\alpha <180°$  thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn.

- Nếu $\alpha =180°$ thì mỗi cung là một nửa đường tròn.

- Cung nằm bên trong góc gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn.

Kí hiệu cung AB là $\stackrel{⏜}{AB}$ .

2. Số đo cung

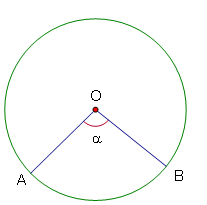
- Số đo của cung $\stackrel{⏜}{AB}$ được kí hiệu là sđ $\stackrel{⏜}{AB}$ .

- Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Ví dụ trên hình vẽ:

$\widehat{AOB}=$sđ  $\stackrel{⏜}{AB}$ nhỏ (góc ở tâm chắn cung $\stackrel{⏜}{AB}$ )

- Số đo cung lớn bằng hiệu giữa $360°$ và số đo của cung nhỏ (có chung hai đầu mút với cung lớn).

- Số đo của nửa đường tròn bằng $180°$ , số đo cả đường tròn bằng $360°$ .

3. So sánh hai cung

Trong một đường tròn hay hai đường tròn bằng nhau:

- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

- Trong hai cung, cung nào có số đo lớn hơn thì được gọi là cung lớn hơn.

Chú ý: Nếu C là một điểm nằm trên cung AB thì

sđ $\stackrel{⏜}{AB}$ = sđ $\stackrel{⏜}{AC}$ + sđ $\stackrel{⏜}{BC}$.

4. Một số định lí liên hệ giữ cung và dây

Định lí 1:

Với hai cung nhỏ trong một đường tròn hay hai đường tròn bằng nhau ta có:

- Hai cung bằng nhau căng hai dây bằng nhau.

- Hai dây bằng nhau căng hai cung bằng nhau.

 Định lí 2:

Với hai cung nhỏ trong một đường tròn hoặc hai đường tròn bằng nhau:

- Cung lớn hơn căng dây lớn hơn.

- Dây lớn hơn căng cung lớn hơn.

Một số định lý khác:

- Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

- Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.

- Trong một đường tròn, đường kính đi qua trung điểm của một dây (dây không đi qua tâm) thì đi qua điểm chính giữa của cung căng bởi dây ấy.

- Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy vừa ngược lại.

II. Các dạng toán

Dạng 1: Bài toán liên quan đến góc ở tâm, số đo cung

Phương pháp giải: Để tính số đo của góc ở tâm, số đo cung bị chắn ta sử dụng các kiến thức sau:

- Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

- Số đo cung lớn bằng hiệu giữa $360°$ và số đo của cung nhỏ (có chung hai đầu mút với cung lớn).

- Số đo của nửa đường tròn bằng $180°$ , số đo cả đường tròn bằng $360°$ .

- Sử dụng tỉ số lượng giác của góc nhọn để tính góc.

- Sử dụng quan hệ đường kính và dây cung.

Ví dụ 1: Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M. Biết $\widehat{AMB}=40°$

a) Tính $\widehat{AOM}$ và $\widehat{AMO}$ .

b) Tính số đo cung $\stackrel{⏜}{AB}$ nhỏ và số đo cung $\stackrel{⏜}{AB}$ lớn.

Lời giải:

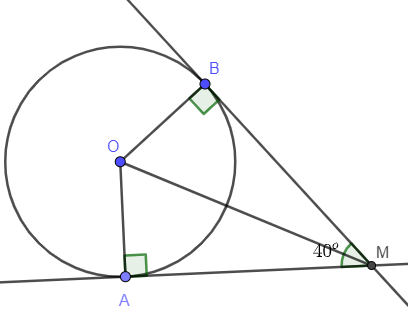
a) Vì AM và BM là hai tiếp tuyến cắt nhau tại M

=> OM là tia phân giác của $\widehat{AMB}$  (tính chất hai tiếp tuyến cắt nhau).

$\Rightarrow \widehat{AMO}=\widehat{BMO}=\frac{\widehat{AMB}}{2}=\frac{40°}{2}=20°$

Vì AM là tiếp tuyến của đường tròn $\Rightarrow OA\perp AM$  (tính chất)

$\Rightarrow \widehat{OAM}=90°$

Xét tam giác AOM có:

$\widehat{OAM}+\widehat{AMO}+\widehat{AOM}=180°$ (định lí tổng ba góc trong một tam giác)

$\iff 90°+20°+\widehat{AOM}=180°$

$\iff \widehat{AOM}=180°-90°-20°$

$\iff \widehat{AOM}=70°$

b) Vì AM và BM là hai tiếp tuyến cắt nhau tại M

=> OM là tia phân giác $\widehat{AOB}$  (tính chất)

$\Rightarrow \widehat{AOM}=\widehat{BOM}=\frac{\widehat{AOB}}{2}$

$\Rightarrow \widehat{AOB}=2\widehat{AOM}\iff \widehat{AOB}=2.70°=140°$

Ta có: $\widehat{AOB}$ là góc ở tâm chắn cung nhỏ $\stackrel{⏜}{AB}$

$\Rightarrow \widehat{AOB}$ = sđ $\stackrel{⏜}{AB}$ nhỏ (định lí góc ở tâm)

=> sđ $\stackrel{⏜}{AB}$ nhỏ = $140°$

Số đo $\stackrel{⏜}{AB}$ lớn là:

$360°$ - sđ $\stackrel{⏜}{AB}$ nhỏ = $360°-140°=220°$

Ví dụ 2: Cho đường tròn (O; R). Vẽ dây AB = $R\sqrt{2}$ . Tính số đo cung nhỏ AB và số đo cung lớn AB.

Lời giải:

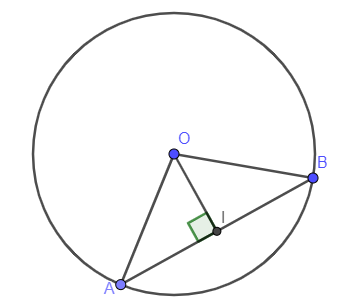
Gọi I là trung điểm của AB

$\Rightarrow OI\perp AB$ (tính chất)

$\Rightarrow \widehat{AIO}=90°$

Vì I là trung điểm của AB nên $IA=IB=\frac{AB}{2}=\frac{R\sqrt{2}}{2}$

Xét tam giác AOI vuông tại I ta có:

$\sin \widehat{AOI}=\frac{AI}{OA}=\frac{\frac{R\sqrt{2}}{2}}{R}=\frac{\sqrt{2}}{2}$

$\Rightarrow \widehat{AOI}=45°$

Xét tam giác AOB có:

OA = OB = R

Do đó tam giác AOB là tam giác cân tại O

=> OI vừa là đường cao vừa là đường phân giác.

$\Rightarrow \widehat{AOB}=2\widehat{AOI}=2.45°=90°$

Mà $\widehat{AOB}$ là góc ở tâm chắn cung nhỏ $\stackrel{⏜}{AB}$

$\Rightarrow \widehat{AOB}$= sđ $\stackrel{⏜}{AB}$ nhỏ (định lí góc ở tâm)

=> sđ $\stackrel{⏜}{AB}$ nhỏ = $90°$

Số đo $\stackrel{⏜}{AB}$ lớn là:

$360°$ - sđ $\stackrel{⏜}{AB}$ nhỏ = $360°-90°=270°$

Dạng 2: Các bài toán liên hệ giữa dây và cung

Phương pháp giải: Để giải các bài toán liên quan đến dây và cung, cần nắm chắc định nghĩa góc ở tâm và kết hợp với liên hệ giữa cung và dây.

Ví dụ 1: Cho đường tròn (O) đường kính AB. Từ A và B vẽ hai dây AC và BD sao cho AC và BD song song với nhau. So sánh số đo hai cung nhỏ $\stackrel{⏜}{AC}$ và $\stackrel{⏜}{BD}$ .

Lời giải:

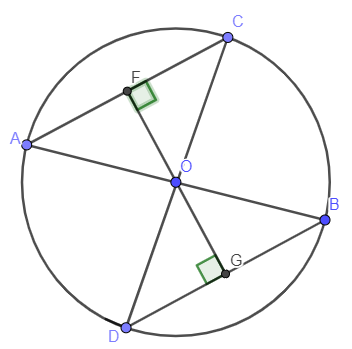
Gọi F là trung điểm của AC; G là trung điểm của BD

$\Rightarrow \left\{\begin{array}{l}O\text{}F\perp AC\\ OG\perp BD\end{array}\right.$

Mà AC // BD nên O, F, G thẳng hàng

Xét $\Delta AOF$ và $\Delta BOG$  có

OA = OB  (bán kính)

$\widehat{AO\text{}F}=\widehat{BOG}$ (hai góc đối đỉnh)

$\widehat{O\text{}FA}=\widehat{OGB}=90°$

Do đó  $\Delta AOF$= $\Delta BOG$ ( cạnh huyền – góc nhọn)

 => AF = BG mà F là trung điểm của AC, G là trung điểm của BD

 => AC = BD

Ta có:

AC là dây căng cung nhỏ $\stackrel{⏜}{AC}$

BD là dây căng cung nhỏ $\stackrel{⏜}{BD}$

Do đó: sđ $\stackrel{⏜}{AC}$ nhỏ = sđ  $\stackrel{⏜}{BD}$ nhỏ (định lý hai day bằng nhau căng hai cung bằng nhau).

Ví dụ 2: Cho tam giác ABC nhọn nội tiếp đường tròn tâm O. Đường cao AH của tam giác ABC cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:

a) BC song song với DE.

b) Tứ giác BCED là hình thang cân.

Lời giải:

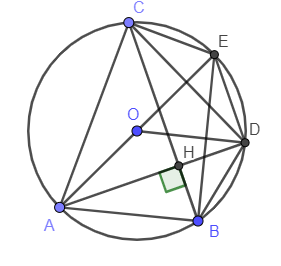
a) Xét tam giác AED có:

O là trung điểm của AE

Mà OA = OE = OD = R

Do đó tam giác AED vuông tại D (tính chất)

$\Rightarrow \widehat{ADE}=90°$

$\Rightarrow DE\perp AD$

Mặt khác $AD\perp BC$

Do đó DE // BC (quan hệ từ vuông góc đến song song)

b) Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau

Do đó:

sđ $\stackrel{⏜}{CE}$ nhỏ = sđ $\stackrel{⏜}{BD}$ nhỏ (nằm giữa hai dây DE và BC song song với nhau)

Lại có:

sđ $\stackrel{⏜}{CE}$ nhỏ + sđ  $\stackrel{⏜}{ED}$ nhỏ  = sđ $\stackrel{⏜}{CD}$ nhỏ   (1)

sđ  $\stackrel{⏜}{BD}$nhỏ + sđ $\stackrel{⏜}{ED}$  nhỏ = sđ $\stackrel{⏜}{BE}$  nhỏ  (2)

Từ (1) và (2) => sđ $\stackrel{⏜}{CD}$  nhỏ = sđ $\stackrel{⏜}{BE}$ nhỏ

=> CD = BE (định lý hai cung bằng nhau căng hai dây bằng nhau)

Xét tứ giác BCED có:

BC // ED

=> Tứ giác BCED là hình thang

Lại có CD = BE nên tứ giác BCED là hình thang cân.

III. Bài tập tự luyện

Bài 1: Cho đường tròn (O) đường kính AB và cung AC có số đo nhỏ hơn $90°$ . Vẽ dây CD vuông góc với AB và dây DE song song với AB. Chứng minh $\stackrel{⏜}{AC}=\stackrel{⏜}{BE}$ .

Bài 2: Cho đường tròn (O) đường kính AB và đường tròn (O’) đường kính AO. Các điểm C, D thuộc đường (O) sao cho $B\in \stackrel{⏜}{CD};\stackrel{⏜}{BC}<\stackrel{⏜}{BD}$ . Các dây AC và AD cắt đường tròn (O’) theo thứ tự tại E và F. Hãy so sánh:

a) Độ dài các đoạn thẳng OE và OF;

b) Số đo các cung $\stackrel{⏜}{AE};\stackrel{⏜}{AF}$  của đường tròn (O).

Bài 3: Trên cung nhỏ $\stackrel{⏜}{AB}$  của (O), cho hai điểm C và D sao cho cung $\stackrel{⏜}{AB}$ được chia thành ba phần bằng nhau $\left(\stackrel{⏜}{AC}=\stackrel{⏜}{CD}=\stackrel{⏜}{DB}\right)$ . Bán kính OC và OD cắt dây AB lần lượt tại E và F.

a) Hãy so sánh độ dài các đoạn thẳng AE và FB.

b) Chứng minh các đường thẳng AB và CD song song.

Bài 4: Cho đường tròn (O; R), lấy điểm M nằm ngoài đường tròn (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến AM và BM với đường tròn (O) (A, B là các tiếp điểm).

a) Tính $\widehat{AOM}$ ;

b) Tính  $\widehat{AOB}$ và số đo cung nhỏ $\stackrel{⏜}{AB}$ .

c) Biết đoạn thẳng OM cắt (O) tại C. Chứng minh C là điểm chính giữa của cung nhỏ $\stackrel{⏜}{AB}$ .

Bài 5: Cho đường tròn (O; R), B là điểm thuộc (O). Gọi H là trung điểm của OB. Dây CD vuông góc với OB tại H. Tính số đo cung nhỏ và cung lớn CD.

Bài 6: Cho đường tròn (O) đường kính AB. Vẽ hai dây AM và BN song song với nhau sao cho sđ $\stackrel{⏜}{BM}<90°$ . Vẽ dây MD song song với AB. Dây DN cắt AB tại E. Từ E vẽ một đường thẳng song song với AM cắt đường thẳng DM tại C. Chứng minh:

a) AB vuông góc với DN.

b) BC là tiếp tuyến của đường tròn (O).

Bài 7: Cho nửa đường tròn (O), đường kính AB và C là điểm chính giữa của nửa đường tròn. Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho $\stackrel{⏜}{CM}=\stackrel{⏜}{BN}$ . Chứng minh:

a) AM = CN.

b) MN = CA = CB.

Bài 8: Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Hãy so sánh các cung nhỏ AB, AC và BC biết $\widehat{A}=50°$ .

Bài 9: Cho đường tròn (O; R) và dây cung MN = $\sqrt{3}R$ . Kẻ OK vuông góc vớ MN tại K. Hãy tính:

a) Độ dài OK theo R.

b) Số đo các góc $\widehat{MOK}$ và $\widehat{MON}$ .

c) Số đo cung nhỏ và cung lớn $\stackrel{⏜}{MN}$ .

Bài 10: Cho đường tròn (O) đường kính AB. Trên cùng nửa đường tròn lấy hai điểm C, D. Kẻ CH vuông góc với AB tại H, CH cắt (O) tại điểm thứ hai là E. Kẻ AK vuông góc với CD tại K, AK cắt (O) tại điểm thứ hai là F. Chứng minh:

a) Hai cung nhỏ $\stackrel{⏜}{CF}$  và $\stackrel{⏜}{BD}$ bằng nhau.

b) Hai cung nhỏ $\stackrel{⏜}{BF}$ và $\stackrel{⏜}{DE}$  bằng nhau.

c) DE = BF.