Công thức về vị trí tương đối của hai đường thẳng hay, chi tiết - Toán lớp 9

1. Các khái niệm

+ Hai đường thẳng song song là hai đường thẳng không có điểm chung.

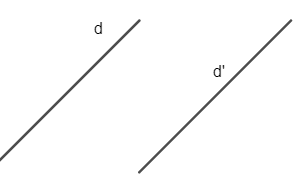
+ Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.

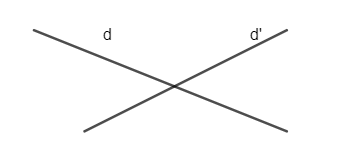
+ Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.

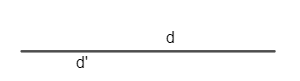
+ Hai đường thẳng vuông góc là hai đường thẳng cắt nhau và trong các góc tạo thành có một góc vuông.

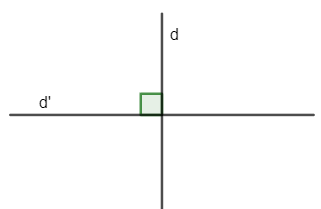
2. Các công thức về vị trí tương đối

Cho đường thẳng d: y = ax + b $\left(a\ne 0\right)$ và đường thẳng d’: y = a’x + b’ $\left(a\text{'}\ne 0\right)$

+ d và d’ song song với nhau khi và chỉ khi

$\left\{\begin{array}{l}a=a\text{'}\\ b\ne b\text{'}\end{array}\right.$

+ d và d’ trùng nhau khi và chỉ khi

$\left\{\begin{array}{l}a=a\text{'}\\ b=b\text{'}\end{array}\right.$

+ d và d’ cắt nhau khi và chỉ khi $a\ne a\text{'}$

+ d và d’ vuông góc với nhau khi và chỉ khi a.a’ = -1.

II. Các ví dụ

Ví dụ 1: Cho đường thẳng d: y = 2x + 5. Xét vị trí tương đối của d với các đường thẳng sau:

a) $d_1$ : y = 2x + 3;

b) $d_2$ : y = 3x – 2;

c) $d_3$ : y = $\frac{-1}{2}x+2$ .

Lời giải:

a) Xét vị trí tương đối của d và $d_1$ ta có:

$\left\{\begin{array}{l}a=a\text{'}=2\\ b\ne b\text{'}\left(5\ne 3\right)\end{array}\right.$

Do đó hai đường thẳng d và $d_1$ song song.

b) Xét vị trí tương đối của d và  $d_2$ta có:

$a=2;a\text{'}=3$

$\Rightarrow a\ne a\text{'}\left(2\ne 3\right)$

Do đó d và $d_2$ cắt nhau.

c) Xét vị trí tương đối của d và $d_3$ ta có:

$a=2;a\text{'}=\frac{-1}{2}$

$\Rightarrow a.a\text{'}=2.\frac{-1}{2}=-1$

Do đó d và $d_3$ vuông góc với nhau.

Ví dụ 2: Viết phương trình đường thẳng d trong các trường hợp sau.

a) d đi qua A(1; 3) và song song với đường thẳng d’: y = 3x – 2.

b) d đi qua B(1; 2) và vuông với với đường thẳng $\Delta$ : y = – 3x + 5.

Lời giải:

a) Gọi đường thẳng d cần tìm là y = ax + b với a $\ne 0$ .

Vì d song song với d’ nên a = 3, b ≠ – 2 .

Đường thẳng d: y = 3x + b

Vì d đi qua A(1; 3) nên ta thay x = 1; y = 3 vào d ta được:

3 = 3.1 + b

$\Rightarrow$b = 0 (t/m)

Vậy đường thẳng d cần tìm là y = 3x.

b) Gọi đường thẳng d cần tìm là y = ax + b với a $\ne 0$ .

Vì d vuông góc với $\Delta$ nên a.a’ = – 1

$\Rightarrow$a.(– 3) = – 1

$\Rightarrow a=\frac{1}{3}$

Đường thẳng d: y = $\frac{1}{3}x+b$

Vì d đi qua B(1; 2) nên thay x = 1; y = 2 vào d ta được:

$2=\frac{1}{3}.1+b$

$\iff 2=\frac{1}{3}+b$

$\iff b=2-\frac{1}{3}$

$\iff b=\frac{5}{3}$

Vậy đường thẳng cần tìm là $d:y=\frac{1}{3}x+\frac{5}{3}$ .