Bài tập về góc tạo bởi tia tiếp tuyến và dây cung - Toán lớp 9

I. Lý thuyết

1. Định nghĩa

- Cho đường tròn (O) có Ax là tia tiếp tuyến tại điểm A và dây cung AB. Khi đó, $\widehat{BAx}$ là góc tạo bởi tia tiếp tuyến và dây cung.

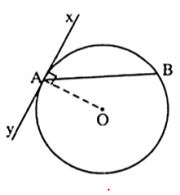
2. Định lí

- Số đo của góc tạo bởi tia tiếp tuyến và dây cung bẳng nửa số đo cung bị chắn.

3. Hệ quả

- Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

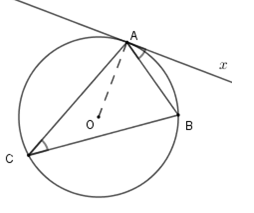
Ta có:

$\widehat{BAx}$ là góc tạo bởi tia tiếp tuyến và dây cung của đường tròn (O) chắn cung $\stackrel{⏜}{AB}$.

$\widehat{ACB}$ là góc nội tiếp của (O) chắn cung $\stackrel{⏜}{AB}$.

$\widehat{BAx}=\widehat{ACB}$.

4. Bổ đề

- Nếu góc $\widehat{BAx}$ với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB có số đo bằng nửa số đo cung bị chắn $\stackrel{⏜}{AB}$ nằm trong góc đó thì Ax là một tia tiếp tuyến của đường tròn.

II. Các dạng bài tập

Dạng 1: Chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đẳng thức hoặc các tam giác đồng dạng

Phương pháp giải:

- Sử dụng hệ quả của góc tạo bởi tia tiếp tuyến và dây cung.

- Sử dụng hệ quả của góc nội tiếp.

- Chứng minh hai cùng bằng góc thứ ba.

- Chứng minh các tam giác bằng nhau.

Ví dụ 1: Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy điểm M. Kẻ tiếp tuyến MN với đường tròn (N là tiếp điểm). Vẽ NH vuông góc với AB. Chứng minh $\widehat{MNA}=\widehat{ANH}$.

Lời giải:

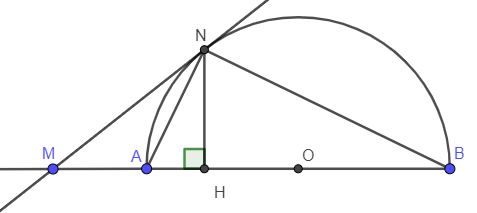
Vì $\widehat{ANB}$ là góc nội tiếp chắn nửa đường tròn (AB là đường kính)

$\Rightarrow \widehat{ANB}$là góc vuông (hệ quả)

Xét tam giác ANH và tam giác ABN có:

$\widehat{A}$ chung

$\widehat{ANB}=\widehat{NHA}=90°$

Do đó $\Delta$ANH đồng dạng với $\Delta$ABN (g – g)

$\Rightarrow \widehat{ANH}=\widehat{ABN}$ (hai góc tương ứng)    (1)

Lại có MN là tiếp tuyến của đường tròn (O) với N là tiếp điểm

$\Rightarrow \widehat{MNA}$ là góc tạo bởi tia tiếp tuyến và dây cung.

$\Rightarrow \widehat{MNA}=\frac{1}{2}\stackrel{⏜}{AN}$  (định lí) (2)

Lại có $\widehat{ABN}$ là góc nội tiếp chắn cung $\stackrel{⏜}{AN}$

$\Rightarrow \widehat{ABN}=\frac{1}{2}\stackrel{⏜}{AN}$ (định lí)  (3)

Từ (2) và (3) $\Rightarrow \widehat{ABN}=\widehat{MNA}$ (4)

Từ (1) và (4) $\Rightarrow \widehat{MNA}=\widehat{ANH}$ (điều phải chứng minh).

Ví dụ 2: Cho đường thẳng d không cắt đường tròn (O), vẽ đường kính CD vuông góc với d tại I. Kẻ tiếp tuyến IA với đường tròn (O). Đường thẳng CA cắt (d) tại B. Chứng minh IA = IB.

Lời giải:

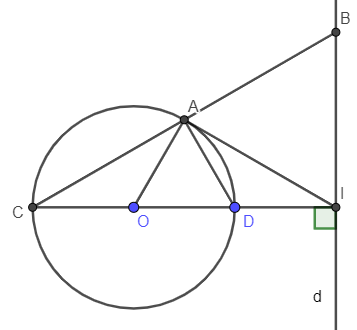
Ta có:

$\widehat{CAD}$ là góc nội tiếp chắn nửa đường tròn (do có CD là đường kính)

$\Rightarrow \widehat{CAD}$ là góc vuông

$\Rightarrow \widehat{CAD}=90°$

Xét tam giác CBI vuông tại I ta có:

$\widehat{BCI}+\widehat{CBI}=90°$ (hai góc nhọn phụ nhau)

$\Rightarrow \widehat{CBI}=90°-\widehat{BCI}$    (1)

Ta có:

$\widehat{DAB}=\widehat{DAI}+\widehat{IAB}$

$\iff 90°=\widehat{DAI}+\widehat{IAB}$

$\Rightarrow \widehat{IAB}=90°-\widehat{DAI}$ (2)

Lại có: $\widehat{ACD}$là góc nội tiếp chắn $\stackrel{⏜}{AD}$

$\widehat{DAI}$ là góc tạo bởi tiếp tuyến và dây cung chắn $\stackrel{⏜}{AD}$.

Do đó:

$\widehat{DAI}=\widehat{ACD}$ ( cùng chắn $\stackrel{⏜}{AD}$) 

Mà A, C, B thẳng hàng và C, D, I thẳng hàng nên

$\widehat{DAI}=\widehat{BCI}$   (3)

Từ (1) (2) (3) $\Rightarrow \widehat{IAB}=\widehat{CBI}$

Xét tam giác AIB có:

$\widehat{IAB}=\widehat{CBI}$

Do đó tam giác AIB cân tại I (dấu hiệu nhận biết)

=> IA = IB (tính chất).

Dạng 2: Chứng minh hai đường thẳng song song, hai đường thẳng vuông góc, một tia là tiếp tuyến của đường tròn

Phương pháp giải:

- Sử dụng hệ quả về góc tạo bởi tia tiếp tuyến và dây cung hoặc hệ quả hai góc nội tiếp.

- Chứng minh tia vuông góc với bán kính để suy ra tiếp tuyến.

Ví dụ 1: Cho đường tròn (O; R) và dây AB (AB < 2R). Gọi P là điểm chính giữa cung nhỏ AB. Gọi C là điểm bất kỳ thuộc dây AB. PC cắt đường tròn tại D. Chứng minh PA là tiếp tuyến của đường tròn ngoại tiếp tam giác ACD.

Lời giải:

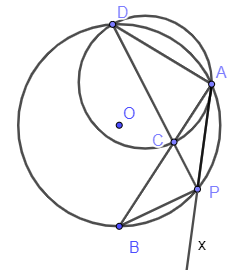
Ta có:

$\widehat{ADP}$ là góc nội tiếp của đường tròn (O) chắn cung $\stackrel{⏜}{AP}$.

$\widehat{BAP}$ là góc nội tiếp của đường tròn (O) chắn cung $\stackrel{⏜}{BP}$

Mà P là điểm chính giữa cung $\stackrel{⏜}{AB}$

=> sđ $\stackrel{⏜}{AP}$ = sđ $\stackrel{⏜}{BP}$

Do đó: $\widehat{ADP}$ = $\widehat{BAP}$ (hệ quả) (*)

Vẽ tia Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ADC với A là tiếp điểm

$\Rightarrow \widehat{CA\text{}x}$ là góc tạo bởi tia tiếp tuyến và dây cung và $\widehat{CA\text{}x}$ chắn cung $\stackrel{⏜}{CA}$

Lại có $\widehat{CDA}$ là góc nội tiếp của đường tròn ngoại tiếp tam giác CDA và $\widehat{CDA}$chắn cung $\stackrel{⏜}{CA}$

Do đó $\widehat{CDA}=\widehat{CAx}$ (hệ quả) (**)

Mà $\widehat{CDA}$ chính là $\widehat{ADP}$. Kết hợp với (*) và (**)

$\Rightarrow \widehat{CA\text{}x}=\widehat{BAP}$

Hay Ax trùng với AP

=> AP là tiếp tuyến của đường tròn ngoại tiếp tam giác ACD với A là tiếp điểm.

Ví dụ 2: Cho đường tròn (O; R), A là điểm cố định trên đường  tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kỳ thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). Gọi I là trung điểm của MA, K là giao điểm của BI với (O).

a) Chứng minh tam giác IKA và tam giác IAB đồng dạng. Từ đó suy ra tam giác IKM đồng dạng với tam giác IMB.

b) Giả sử MK cắt (O) tại C. Chứng minh BC song song với MA.

Lời giải:

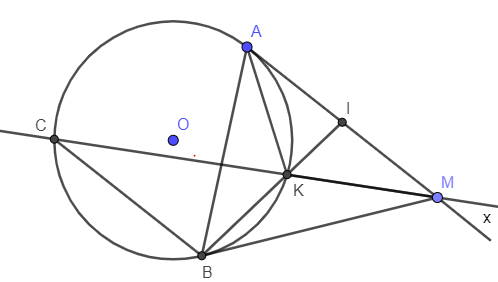
a) Ta có:

$\widehat{ABK}$ là góc nội tiếp chắn cung $\stackrel{⏜}{AK}$  (1)

$\widehat{KAI}$ là góc tạo bởi tia tiếp tuyến và dây cung chắn cung $\stackrel{⏜}{AK}$   (2)

Từ (1) và (2) $\Rightarrow \widehat{ABK}=\widehat{KAI}$(hệ quả)

Xét tam giác IKA và tam giác IAB có:

$\widehat{AIK}$ chung

$\widehat{ABK}=\widehat{KAI}$ (chứng mnh trên)

Do đó $\Delta$IKA $~$$\Delta$IAB (g – g)

Chứng minh tương tự ta sẽ được $\Delta$IKM$~$$\Delta$IMB (c – g – c).

b) Từ câu a ta có $\Delta$IKM$~$$\Delta$IMB $\Rightarrow \widehat{IMK}=\widehat{KBM}$(hai góc tương ứng)   (3)

Lại có:

$\widehat{BCK}$ là góc nội tiếp chắn cung $\stackrel{⏜}{BK}$

$\widehat{KBM}$ là góc tạo bởi tia tiếp tuyến và dây cung chắn cung $\stackrel{⏜}{BK}$

Do đó $\widehat{BCK}=\widehat{KBM}$(4)

Từ (3) và (4) $\Rightarrow \widehat{IMK}=\widehat{BCK}$

Mà hai góc này ở vị trí so le trong nên hai đường thẳng BC và AM song song với nhau.

III. Bài tập tự luyện

Bài 1: Cho điểm A nằm ngoài đường tròn (O). Qua A kẻ hai tiếp tuyến AB; AC với (O), B; C là hai tiếp điểm. Kẻ cát tuyến AMN với (O) (M nằm giữa A và N)

a) Chứng minh: $A{B}^2=AM.AN$

b) Gọi H là giao điểm của AO và BC. Chứng minh AH.AO = AM.AN.

c) Đoạn thẳng AO cắt đường tròn (O) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác ABC.

Bài 2: Cho đường tròn (O) ngoại tiếp tam giác ABC. Tiếp tuyến tại A cắt BC ở I.

a) Chứng minh: $\frac{IB}{IC}=\frac{A{B}^2}{A{C}^2}$.

b) Tính IA; IC biết AB = 20cm; AC = 28cm; BC = 24cm.

Bài 3: Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A của (O) cắt BC tại P.

a) Chứng minh tam giác PAC và tam giác PBA đồng dạng.

b) Chứng minh $P{A}^2=PB.PC$.

c) Tia phân giác trong của góc A cắt BC và (O) lần lượt tại D và M. Chứng minh $M{B}^2=MA.MD$.

Bài 4: Cho tam gác ABC nội tiếp đường tròn (O), At là tiếp tuyến của đường tròn (O). Đường thẳng song song với At cắt AB và AC lần lượt tại M và N. Chứng minh AB.AM = AC.AN.

Bài 5: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ tiếp tuyến Ax với (O) và cắt (O’) tại E. Qua A vẽ tiếp tuyến Ay với (O’) cắt (O) tại D. Chứng minh $A{B}^2=BD.BE$.

Bài 6: Cho hình thang ABCD (AB / CD) có $B{D}^2=AB.CD$. Chứng minh đường tròn ngoại tiếp tam giác ABD tiếp xúc với BC.

Bài 7: Cho hình vuông ABCD có cạnh 2cm. Tính bán kính của đường tròn đi qua A và B biết rằng đoạn tiếp tuyến kẻ từ D đến đường tròn đó bằng 4cm.

Bài 8: Cho tam giác ABC nội tiếp đường tròn (O) và AB < AC. Đường tròn (I) đi qua B và C, tiếp xúc với AB tại B cắt đường thẳng AC tại D. Chứng minh OA và BD vuông góc với nhau.

Bài 9: Cho hai đường tròn (O) và (I) cắt nhau ở C và D, trong đó tiếp tuyến chung MN song song với cát tuyến EDF, M và E thuộc (O), N và F thuộc (I), D nằm giữa E và F. Gọi K, H theo thứ tự là giao điểm của NC, MC với EF. Gọi G là giao điểm của EM, FN. Chứng minh:

a) Tam giác GMN và tam giác DMN bằng nhau.

b) GD là đường trung trực của KH.

Bài 10: Cho hình bình hành ABCD, $\widehat{A}\le 90°$. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng minh BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB.