Cách xác định đường tròn và tính chất đối xứng của đường tròn - Toán lớp 9

I. Lý thuyết

1. Định nghĩa đường tròn

Đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng không đổi là R (R > 0).

Kí hiệu: (O) hoặc (O; R)

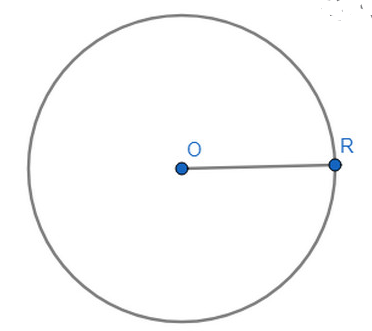
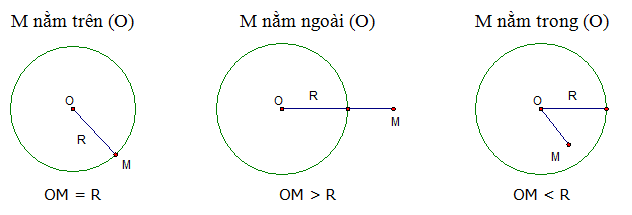
2. Vị trí tương đối của điểm M và đường tròn tâm O bán kính R

- Điểm M nằm trên đường tròn tâm O bán kính R nếu OM = R.

- Điểm M nằm trong đường tròn tâm O bán kính R nếu OM < R.

- Điểm M nằm ngoài đường tròn tâm O bán kính R nếu OM > R.

3. Một số định lý về xác định đường tròn

- Đường tròn được xác định khi biết tâm và bán kính của đường tròn đó, hoặc khi biết một đoạn thẳng là đường kính của đường tròn đó.

- Ta chỉ vẽ được một và chỉ một đường tròn duy nhất qua 3 điểm không thẳng hàng.

Chú ý: Không vẽ được đường tròn đi qua 3 điểm không thẳng hàng

- Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác. Khi đó, ta gọi tam giác là tam giác nội tiếp đường tròn. Tâm của đường tròn là giao điểm  của ba đường trung trực của tam giác.

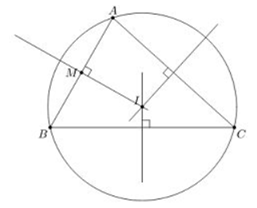
Cho tam giác ABC có I là giao của ba đường trung trực của tam giác

Khi đó đường tròn tâm I bán kính IA là đường tròn duy nhất đi qua 3 đỉnh của tam giác.

- Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền.

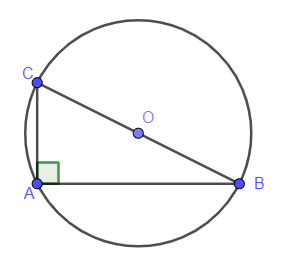
Tam giác ABC vuông tại A. Đường tròn ngoại tiếp tam giác ABC là đường tròn (O) với O là trung điểm cạnh BC.

- Đường tròn ngoại tiếp tam giác đều có tâm là trong tâm của tam giác

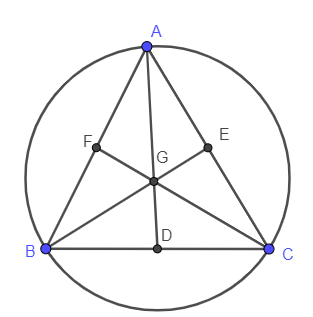
Tam giác ABC là tam giác đều. G là trọng tâm tam giác nên G là tâm đường tròn ngoại tiếp tam giác.

4. Tính chất đối xứng của đường tròn

- Đường tròn là hình có tâm đối xứng và trục đối xứng.

- Tâm đối xứng là tâm đường tròn.

- Trục đối xứng là bất kỳ đường kính nào của đường tròn.

II. Các dạng bài tập

Dạng 1: Chứng minh các điểm cho trước cùng nằm trên một đường tròn

Phương pháp giải: Ta có hai cách để chứng minh sau

Cách 1: Chứng minh các điểm cho trước cùng cách đều một điểm nào đó.

Cách 2: Dùng định lý: “Nếu một tam giác có một cạnh là đường kính đường tròn ngoại tiếp tam giác đó thì tam giác đó là tam giác vuông và ba đỉnh của tam giác đó nằm trên đường tròn có đường kính là cạnh huyền của tam giác đó.”

Ví dụ 1: Cho tam giác ABC vuông tại A. Chứng minh tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của BC.

Lời giải:

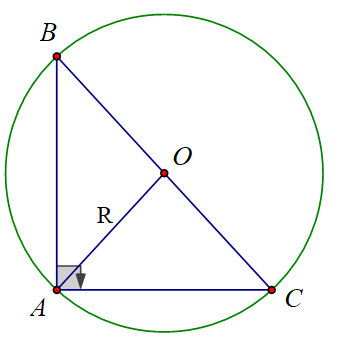
Gọi O là trung điểm của BC

$\Rightarrow BO=CO=\frac{1}{2}BC$ (1)

Lại có: Tam giác ABC vuông tại A

AO là đường trung tuyến ứng với cạnh huyền

Do đó $AO=\frac{1}{2}BC$ (2)

Từ (1) và (2) $\Rightarrow BO=CO=AO=\frac{1}{2}BC$

$\Rightarrow$ ba điểm A, B, C cách đều O hay A, B, C nằm trên đường tròn tâm O bán kính OA

Vậy O là là tâm đường tròn ngoại tiếp tam giác ABC (điều phải chứng minh).

Ví dụ 2: Cho tam giác ABC, các đường cao BH và CK. Chứng minh bốn điểm B, H, C, K thuộc cùng một đường tròn. Xác định tâm và bán kính đường tròn đó.

Lời giải:

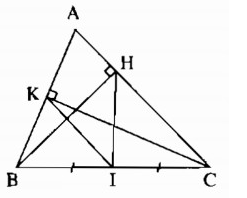
Gọi I là trung điểm của BC. Ta sẽ chứng minh bốn điểm B, K, H, C thuộc một đường tròn tâm I

Xét tam giác BKC vuông tại K, trung tuyến KI ta có:

$BI=IC=IK=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền) (1)

Xét tam giác BHC vuông tại H, trung tuyến HI ta có:

$BI=IC=IH=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền) (2)

Từ (1) và (2) $\Rightarrow BI=IC=IH=IK=\frac{1}{2}BC$

$\Rightarrow$B, H, K, C cùng cách đều I

$\Rightarrow$B, H, C, K thuộc đường tròn tâm I bán kính IB.

Ví dụ 3: Cho hình thoi ABCD. Đường trung trực cạnh AB cắt BD tại E và cắt AC tại F. Chứng minh E, F lần lượt là tâm đường tròn ngoại tiếp tam giác ABC và tam giác ABD.

Lời giải:

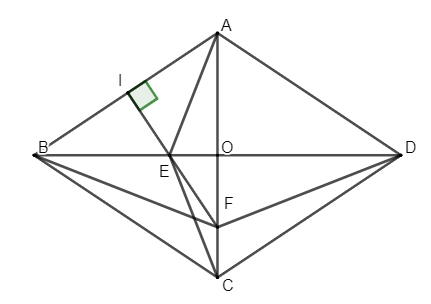
Gọi I là trung điểm của AB

* Chứng minh E là tâm đường tròn ngoại tiếp tam giác ABC

Gọi O là giao điểm của AC và BD.

$\Rightarrow$O là trung điểm của AC (tính chất hình thoi)

$\Rightarrow$BO là đường trung tuyến của tam giác ABC

Lại có ABCD là hình thoi nên AB = BC

$\Rightarrow$Tam giác ABC cân tại B

$\Rightarrow$BO là đường trung trực của tam giác ABC (tính chất)

Ta có:

BO là đường trung trực của tam giác ABC ứng với cạnh AC; FI là đường trung trực của tam giác ABC ứng với cạnh AB

$\Rightarrow$Giao điểm của BO và FI là tâm đường tròn ngoại tiếp tam giác ABC.

Mà $BO\cap FI$ tại điểm E

$\Rightarrow$E là tâm đường tròn ngoại tiếp tam giác ABC.

* Chứng minh F là tâm đường tròn ngoại tiếp tam giác ABD

Xét tam giác BFO và tam giác DFO có:

FO chung

BO = DO (O là trung điểm của BD)

$\widehat{FOB}=\widehat{FOD}=90°$ (tính chất hai đường chéo của hình thoi)

Do đó $\Delta BFO=\Delta DFO$ (c – g – c)

$\Rightarrow$BF = DF (1)

Vì FI là đường trung trực của AB nên F cách đều A và B

$\Rightarrow FA=FB$(2)

Từ (1) và (2) $\Rightarrow FA=FB=FD$

$\Rightarrow$ba điểm A, B, D cách đều F

$\Rightarrow$F là tâm đường tròn ngoại tiếp tam giác ABD.

Dạng 2: Xác định vị trí tương đối của một điểm với một đường tròn

Phương pháp giải: Muốn xác định vị trí của M với đường tròn tâm O ta so sánh OM với bán kính sẽ xảy ra một trong ba trường hợp sau.

- Điểm M nằm trên đường tròn tâm O bán kính R nếu OM = R.

- Điểm M nằm trong đường tròn tâm O bán kính R nếu OM < R.

- Điểm M nằm ngoài đường tròn tâm O bán kính R nếu OM > R.

Ví dụ 1: Cho tam giác ABC đều cạnh bằng a. Các đường cao BH và CK. Gọi O là trung điểm của BC.

a) Chứng minh: B, H, C, K thuộc một đường tròn tâm O.

b) Gọi G là giao điểm của BH và CK. Chứng minh điểm G nằm trong, điểm A nằm ngoài đường tròn đường kính BC.

Lời giải:

a) Xét tam giác BKC vuông tại K, trung tuyến KO ta có:

$BO=OC=OK=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền) (1)

Xét tam giác BHC vuông tại H, trung tuyến HO ta có:

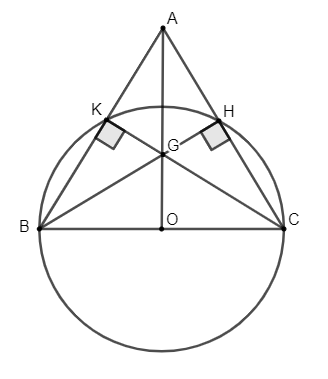
$BO=OC=OH=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền) (2)

Từ (1) và (2) $\Rightarrow BO=OC=OH=OK=\frac{1}{2}BC$

$\Rightarrow$B, H, K, C cùng cách đều O

$\Rightarrow$B, H, C, K thuộc đường tròn tâm O đường kính BC

b) Vì tam giác ABC là tam giác đều nên BH và CK cũng là đường trung tuyến

nên G là trọng tâm tam giác ABC.

$\Rightarrow$A, O, G thẳng hàng

Lại có AO là đường trung tuyến $\Rightarrow$AO$\perp$BC (tính chất tam giác đều)

Xét tam giác AOB vuông tại O ta có:

$A{O}^2+B{O}^2=A{B}^2$(định lý py - ta - go)

Với AB = a; $BO=\frac{1}{2}BC=\frac{a}{2}$thay vào ta có:

$A{O}^2+{\left(\frac{a}{2}\right)}^2=a^2$

$\iff A{O}^2+\frac{a^2}{4}=a^2$

$\iff A{O}^2=a^2-\frac{a^2}{4}$

$\iff A{O}^2=\frac{3a^2}{4}$

$\iff AO=\frac{\sqrt{3}}{2}a$

Vì  AO > BO $\left(\frac{\sqrt{3}}{2}a>\frac{1}{2}a\right)$ nên A nằm ngoài đường tròn tâm O đường kính BC

Lại có:

$OG=\frac{1}{3}AO$

$\iff OG=\frac{1}{3}.\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{6}a$

Vì OG  < OB $\left(\frac{\sqrt{3}}{6}a<\frac{1}{2}a\right)$nên G nằm trong đường tròn tâm O đường kính BC.

Ví dụ 2: Cho đường tròn (O) đường kính AD = 2R. Vẽ đường tròn tâm D bán kính  R, đường tròn này cắt đường tròn tâm O ở B và C.

Tứ giác OBDC là hình gì? Vì sao?

Lời giải:

Xét đường tròn (O) có đường kính là AD = 2R

$\Rightarrow$Bán kính là OD = R

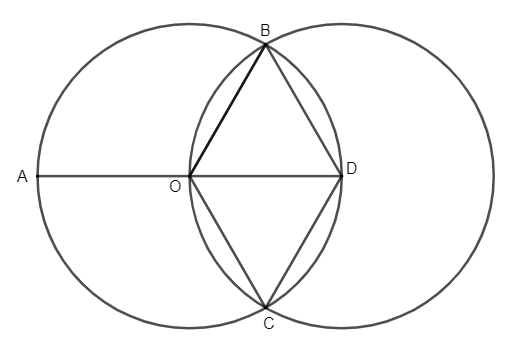
Vì B là giao của (O; R) và (D; R) nên ta có:

$\left\{\begin{array}{l}B\in (O;R)\\ B\in \left(D;R\right)\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}OB=R\\ DB=R\end{array}\right.$(1)

Vì C là giao của (O; R) và (D; R) nên ta có:

$\left\{\begin{array}{l}C\in (O;R)\\ C\in \left(D;R\right)\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}OC=R\\ DC=R\end{array}\right.$ (2)

Từ (1) và (2) $\Rightarrow$OB = OC = BD = DC = R

Xét tứ giác OBCD có:

OB = OC = BD = DC
$\Rightarrow$Tứ giác OBDC là hình thoi (dấu hiệu nhận biết).

Dạng 3: Xác định tâm, bán kính đường tròn ngoại tiếp tam giác và số đo các góc liên quan

Phương pháp giải:

- Sử dụng định lý py – ta – go.

- Sử dụng định lí đường trung tuyến ứng với cạnh huyền trong tam giác vuông.

- Sử dụng hệ thức về cạnh và góc trong tam giác vuông.

Ví dụ 1: Cho tam giác ABC vuông tại A, có AB = 4; AC = 3. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

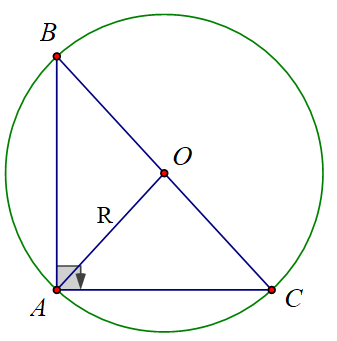
Gọi O là trung điểm của BC.

Xét tam giác ABC vuông tại A

Khi đó O là tâm đường tròn ngoại tiếp tam giác ABC (định lí)

Theo định lý Py – ta – go trong tam giác ABC vuông, ta có:

$A{B}^2+A{C}^2=B{C}^2$

$\iff 4^2+3^2=B{C}^2$

$\iff B{C}^2=16+9$

$\iff B{C}^2=25$

$\Rightarrow BC=5$

Lại có:

Bán kính đường tròn ngoại tiếp tam giác vuông ABC là BO

$\Rightarrow$BO = BC:2 = 5:2 = 2,5.

Ví dụ 2: Cho góc $\widehat{xAy}=60°$ và điểm B trên tia Ay sao cho AB = 3cm.

a) Dựng đường tròn tâm O đi qua 2 điểm A và B sao cho tâm O thuộc tia Ox

b) Tính bán kính đường tròn tâm O.

Lời giải:

a) Gọi I là trung điểm của AB, ta dựng đường trung trực của AB

Đường trung trực của AB cắt Ox tại O

O là tâm đường tròn đi qua A và B và tâm O thuộc Ox

Chứng minh:

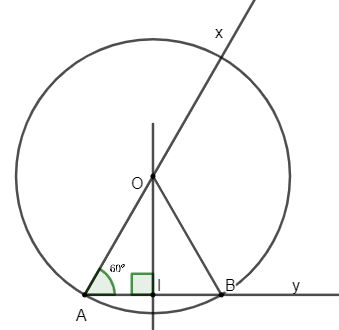
Vì O nằm trên đường trung trực của AB nên O cách đều A và B

$\Rightarrow$OA = OB

Lại có O là giao điểm của đường trung trực của AB và Ax nên ta dựng được đường tròn cần tìm

b) Gọi I là trung điểm của AB

$\Rightarrow$AI = IB = AB:2 = 1,5

Xét tam giác vuông AOI vuông tại I ta có:

$\cos \widehat{OAI}=\frac{AI}{AO}$

$\cos 60°=\frac{1,5}{AO}=\frac{1}{2}$

$\Rightarrow AO=1,5.2=3$

Vậy bán kính đường tròn cần tìm là OA = 3cm

Cách 2: Tam giác OAB có OA = OB (câu a) nên ∆OAB cân tại A

Mà $\widehat{OAB}=\widehat{xAy}=60°$

Do đó ∆OAB đều nên OA = OB = AB = 3 cm.

Vậy bán kính đường tròn cần tìm là OA = 3 cm.

III. Bài tập vận dụng

Phần 1: Bài tập trắc nghiệm

Câu 1: Đường tròn có bao nhiêu trục đối xứng

A. 1                      B. 2                      C. Không có                   D. Vô số

Câu 2: Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Bán kính đường tròn ngoại tiếp tam giác ABC là:

A. 3cm                  B. 4cm                  C. 5cm                                     D. 6cm

Câu 3: Nếu tam giác ABC là tam giác tù thì tâm đường tròn ngoại tiếp tam giác ABC nằm ở đâu

A. Bên trong tam giác

B. Bên ngoài tam giác

C. Nằm trên cạnh dài nhất trong ba cạnh tam giác

D. Nằm trên cạnh ngắn nhất trong ba cạnh tam giác

Câu 4: Cho hình vuông ABCD. Tâm đường tròn đi qua bốn đỉnh của hình vuông là

A. Giao điểm của hai đường chéo

B. Không xác định được

C. Trung điểm của cạnh DC

D. Trọng tâm tam giác ABC

Câu 5: Khẳng định nào sau đây sai:

A. Vẽ được đường tròn đi qua cả ba điểm thẳng hàng

B. Qua ba điểm không thẳng hàng ta vẽ được duy nhất một đường tròn qua ba điểm đó.

C. Tâm đối xứng của đường tròn là tâm của đường tròn đó.

D. Có vô số trục đối xứng của hình tròn

Phần 2: Tự luận

Bài 1: Cho tam giác ABC cân tại A. Đường cao AH = 2cm, BC = 8cm. Đường thẳng vuông góc với AC tại C cắt đường thẳng AH tại D.

a) Chứng minh bốn điểm A, B, C, D thuộc cùng một đường tròn.

b) Tính độ dài AD.

Bài 2: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh M, N, P, Q thuộc cùng một đường tròn.

Bài 3: Cho tam giác ABC có đường cao AD và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC và AC. Chứng minh:

a) Bốn điểm E, F, I, K cùng thuộc một đường tròn.

b) Điểm D cũng thuộc đường tròn đi qua bốn điểm E, F, I, K.

Bài 4: Cho hình chữ nhật ABCD có AB = 9 cm; BC = 12 cm. Chứng minh bốn điểm ABCD thuộc cùng một đường tròn và tính bán kính đường tròn đó.

Bài 5: Cho tam giác ABC nhọn. Vẽ đường tròn (O)  có đường kính BC, cắt AB, AC theo thứ tự D và E.

a) Chứng minh: $CD\perp AB$ và $BE\perp AC$

b) Gọi K là giao điểm của BE và CD. Chứng minh $BC\perp AK$

Bài 6: Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. E là giao điểm của CM và DN.

a) Tính số đo góc CEN.

b) Chứng minh A, D, E, M thuộc cùng một đường tròn.

c) Xác định tâm đường tròn đi qua ba điểm B, D, E.

Bài 7: Cho đường tròn (O) đường kính AB, điểm C chạy trên đường tròn. H là hình chiếu của C lên AB. Trên OC lấy M sao cho OM = OH.

a) Khi C di chuyển thì M chạy trên đường nào?

b) Trên BC lấy D sao cho CD = CB. Hỏi khi C thay đổi điểm D chạy trên đường nào?

Đáp án trắc nghiệm