Phương trình bậc nhất hai ẩn và tập nghiệm và cách giải bài tập - Toán lớp 9

I. Lý thuyết

1. Khái niệm phương trình bậc nhất hai ẩn

- Phương trình bậc nhất hai ẩn x, y là phương trình có dạng: ax + by = c

trong đó a, b, c là các số cho trước, $a\ne 0;b\ne 0$.

- Nếu số thực $x_0;y_0$ thỏa mãn $a{x}_0+b{y}_0=c$ thì cặp số $\left(x_0;y_0\right)$ được gọi là nghiệm của phương trình ax + by = c.

- Trong mặt phẳng tọa độ Oxy, mỗi nghiệm $\left(x_0;y_0\right)$ của phương trình ax + by = c được biểu diễn bởi điểm có tọa độ $\left(x_0;y_0\right)$.

2. Tập nghiệm của phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn ax + by =c luôn có vô số nghiệm.

Tập nghiệm của phương trình biểu diễn bởi đường thẳng d: ax + by = c

- Nếu $a\ne 0$ và b = 0 thì phương trình có nghiệm $\left\{\begin{array}{l}x=\frac{c}{a}\\ y\in ℝ\end{array}\right.$ và đường thẳng d song song hoặc trùng với trục tung.

- Nếu a = 0 và $b\ne 0$ thì phương trình có nghiệm $\left\{\begin{array}{l}x\in ℝ\\ y=\frac{c}{b}\end{array}\right.$ và đường thẳng d song song hoặc trùng với trục hoành.

- Nếu $a\ne 0;b\ne 0$ thì phương trình có nghiệm $\left\{\begin{array}{l}x\in ℝ\\ y=\frac{-a}{b}x+\frac{c}{b}\end{array}\right.$ hoặc $\left\{\begin{array}{l}y\in ℝ\\ x=\frac{-b}{a}y+\frac{c}{a}\end{array}\right.$ khi đó đường thẳng d cắt cả hai trục Ox; Oy. Đường thẳng d là đồ thị hàm số $y=\frac{-a}{b}x+\frac{c}{b}$.

II. Dạng bài tập và phương pháp giải

Dạng 1: Xét một cặp số cho trước có là nghiệm của phương trình bậc nhất hai ẩn không

Phương pháp giải: Nếu cặp số thực $\left(x_0;y_0\right)$ thỏa mãn $a{x}_0+b{y}_0=c$ thì nó được gọi là nghiệm của phương trình ax + by = c.

Ví dụ 1: Trong các cặp số (12; 1); (1; 1); (2; -3) cặp số nào là nghiệm của phương trình 2x – 5y =19.

Lời giải:

- Xét cặp số (12; 1)

Thay x = 12 và y = 1 ta có:

2.12 -1.5 = 24 – 5 = 19 nên cặp số (12; 1) là nghiệm của phương trình 2x – 5y = 19.

- Xét cặp số (1; 1) ta có:

Thay x = 1; y = 1 ta có:

2.1 – 5.1 = -3 nên cặp số (1; 1) không là nghiệm của phương trình 2x – 5y =19.

- Xét cặp số (2; -3)

Thay x = 2 và y = -3 ta có:

2.2 – 5.(-3) = 4 + 15 = 19 nên căp số (2; -3) là nghiệm của phương trình 2x – 5y = 19.

Ví dụ 2: Viết phương trình bậc nhất hai ẩn có hai nghiệm là (2; 0) và (-1; -2).

Lời giải:

Vì nghiệm của phương trình bậc nhất hai ẩn nằm trên một đường thẳng nên ta gọi đường thẳng đó là d: y = ax + b.

+ Thay x = 2; y = 0 vào đường thẳng d ta có: 0 = 2.a + b (1)

+ Thay x = -1; y = -2 vào đường thẳng d ta có: -2 = -1.a + b (2)

Từ (2) ta có: b = -2 + a thay vào (1) ta có:

2.a + a – 2 =0

$\iff$3a – 2 = 0

$\iff$3a = 2

$\iff a=\frac{2}{3}$$\Rightarrow b=-2+\frac{2}{3}=\frac{-4}{3}$

Đường thẳng d cần tìm là y = $\frac{2}{3}$x$-\frac{4}{3}$

$\Rightarrow$Phương trình bậc nhất hai ẩn là 2x – 3y – 4 = 0.

Dạng 2: Viết công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn và biểu diễn tập nghiệm phương trình trên mặt phẳng tọa độ

Phương pháp giải: Xét phương trình bậc nhất hai ẩn ax + by + c = 0.

- Để viết công thức nghiệm tổng quát của phương trình, trước tiên ta biểu diễn x theo y (hoặc y theo x) rồi đưa ra kết luận về công thức nghiệm tổng quát.

- Để biểu diễn tập nghiệm phương trình trên mặt phẳng tọa độ, ta vẽ đường thẳng d có phương trình ax + by = c trên mặt phẳng tọa độ.

Ví dụ 1: Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau:

a) 2x – 3y = 5

b) 4x +0y =12.

Lời giải:

a) Xét phương trình 2x – 3y = 5 ta có:

$a\ne 0;b\ne 0$ (do a = 2; b = -3) nên ta có công thức nghiệm của phương trình là

$\left\{\begin{array}{l}x\in ℝ\\ y=\frac{-a}{b}x+\frac{c}{b}\end{array}\right.$$\iff \left\{\begin{array}{l}x\in ℝ\\ y=\frac{2}{3}x-\frac{5}{3}\end{array}\right.$

Vẽ đường thẳng $y=\frac{2}{3}x-\frac{5}{3}$ trên hệ mặt phẳng tọa độ.

Cho x = 0 $\Rightarrow y=\frac{-5}{3}$$\Rightarrow A\left(0;\frac{-5}{3}\right)$

Cho y = 0$\Rightarrow x=\frac{5}{2}\Rightarrow B\left(\frac{5}{2};0\right)$

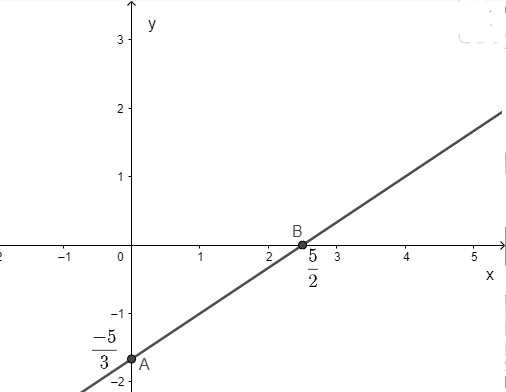
Nghiệm của phương trình 2x – 3y = 5 là đường thẳng được biểu diễn trên hình vẽ.

b) Xét phương trình 4x + 0y = 12

$a\ne 0;b=0$ (do a = 4; b = 0) nên ta có công thức nghiệm của phương trình là

$\left\{\begin{array}{l}x=\frac{c}{a}\\ y\in ℝ\end{array}\right.$$\iff \left\{\begin{array}{l}x=\frac{12}{4}=3\\ y\in ℝ\end{array}\right.$

Vẽ đường thẳng x = 3 trên hệ mặt phẳng tọa độ.

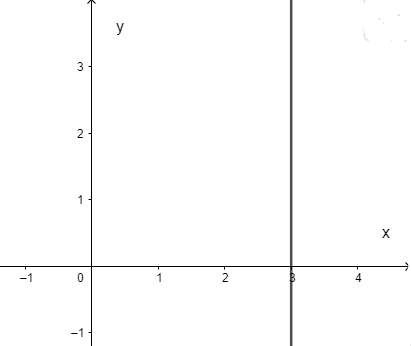
Dạng 3: Tìm điều kiện của tham số để đường thẳng thỏa mãn điều kiện cho trước

Phương pháp giải: Ta có thể sử dụng một số lưu ý sau đây để giải dạng toán này.

- Nếu $a\ne 0$ và b = 0 thì phương trình đường thẳng d: ax + by = c có dạng d: $x=\frac{c}{a}$khi đó d song song hoặc trùng với Oy.

- Nếu a = 0 và $b\ne 0$ thì phương trình đường thẳng d: ax + by = c có dạng d: $y=\frac{c}{b}$khi đó d song song hoặc trùng với Ox.

- Nếu $a\ne 0;b\ne 0$ thì phương trình đường thẳng d: ax + by = c có dạng d: $y=\frac{-a}{b}x+\frac{c}{b}$.

- Đường thẳng d: ax + by = c đi qua điểm $M\left(x_0;y_0\right)$ khi và chỉ khi $a{x}_0+b{y}_0=c$.

Ví dụ 1:  Cho đường thẳng d có phương trình: (m – 2)x + (3m – 1)y = 6m – 2

Tìm m để:

a) d song song hoặc trùng với trục hoành.

b) d song song hoặc trùng với trục tung

c) d đi qua điểm A(1; -1).

Lời giải:

a) Để d song song với trục hoành

$\iff \left\{\begin{array}{l}a=0\\ b\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}m-2=0\\ 3m-1\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}m=2\\ 3m\ne 1\end{array}\right.$

$\iff \left\{\begin{array}{l}m=2\\ m\ne \frac{1}{3}\end{array}\right.$

Vậy m = 2 thì d song song với trục hoàng.

b) Để d song song với trục tung $\iff \left\{\begin{array}{l}a\ne 0\\ b=0\end{array}\right.$

$\iff \left\{\begin{array}{l}m-2\ne 0\\ 3m-1=0\end{array}\right.$

$\iff \left\{\begin{array}{l}m\ne 2\\ 3m=1\end{array}\right.$

$\iff \left\{\begin{array}{l}m\ne 2\\ m=\frac{1}{3}\end{array}\right.$

Vậy $m=\frac{1}{3}$thì d song song với trục tung.

c) d đi qua A(1; -1). Thay x = 1; y = -1 và d ta có:

(m - 2).1 + (3m – 1).(-1) = 6m – 2

$\iff m-2-3m+1=6m-2$

$\iff m-3m-2+1-6m+2=0$

$\iff -8m+1=0$

$\iff -8m=-1$

$\iff m=\frac{1}{8}$

Vậy $m=\frac{1}{8}$ thì d đi qua A(1; -1)

III. Bài tập tự luyện

Bài 1: Cặp số (-2; 3) là nghiệm của phương trình nào trong các phương trình dưới đây?

a) x – y = 1

b) 2x + 3y = 5

c) 2x + y = 7

d) 2x – y = -7

Bài 2: Trong các cặp số (1; 3); (-2; 0); (0; 4); (3; 2) cắp số nào là nghiệm của phương trình 2x + 2y = 8.

Bài 3: Tìm các giá trị của m để phương trình bậc nhất hai ẩn $\sqrt{m+1}x-2y=m+1$có một nghiệm là (1; -1).

Bài 4: Cho hai nghiệm của một phương trình bậc nhất hai ẩn là (2; 3) và (4; 6). Tìm phương trình bậc nhất hai ẩn đó.

Bài 5: Viết công thức tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ:

a) 3x – y = 5

b) 2x + 0y = 6

c) 0x + 3y = 9.

Bài 6: Cho đường thẳng d có phương trình:

(2m – 1)x +3(m – 1)y = 4m – 2

Tìm các tham số m để

a) d song song với Ox

b) d song song với Oy

c) d đi qua gốc tọa độ

d) d đi qua điểm A(2; 1).

Bài 7: Tìm giá trị của tham số m để cặp số $\left(\frac{-3}{2};2\right)$ là nghiệm của phương trình:

 (m – 3)x +2my = 5 + m

Bài 8: Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ:

a) x – 2y = 7

b) 3x – 2y = 3

c) 7x + 0y = 14.

Bài 9: Tìm phương trình đường thẳng d biết d đi qua hai điểm M(-1; -3) và N(2; 1).

Bài 10: Cho đường thẳng d có phương trình:

(2m – 3)x + (3m – 1)y = m + 2

a) d song song với Ox

b) d song song với Oy

c) d đi qua gốc tọa độ

d) d đi qua A(2; 3).