Vị trí tương đối của hai đường tròn đầy đủ, chi tiết - Toán lớp 9

I. Lý thuyết

Cho hai đường tròn (O; R) và (O’; r) với R > r

1. Hai đường tròn (O) và (O’) cắt nhau

+ Hai đường tròn cắt nhau thì R – r < d < R + r và hai đường tròn (O) và (O’) có 2 điểm chung

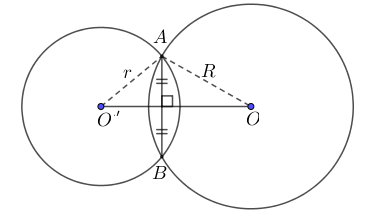
+ Điểm chung của (O) và (O’) là A và B.

+ Đường nối hai tâm là đường trung trực của đoạn thẳng nối hai giao điểm.

2. Hai đường tròn (O) và (O’) tiếp xúc nhau

+ Tiếp xúc trong: d = R – r

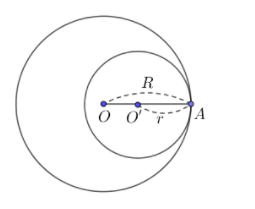
Điểm chung của O và O’ là A và O’ nằm giữa O và A

+ Tiếp xúc ngoài: d = R + r

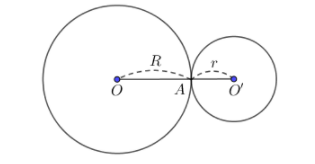
(O) và (O’) có một điểm chung là A và A nằm giữa O và O’.

3. Hai đường tròn (O) và (O’) không giao nhau

+ (O) và (O’) nằm ngoài nhau: d > R + r

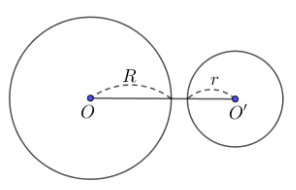
+ (O) đựng (O’): d < R – r

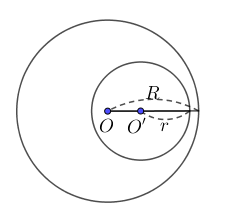
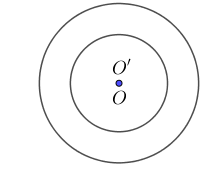
+ (O) và (O’) đồng tâm: d = 0

II. Các ví dụ

Ví dụ 1: Cho hai đường tròn (O; 4cm) và (O’; 11cm). Biết OO’ = 2a + 3 cm. Tìm a để (O) và (O’) tiếp xúc nhau.

Lời giải:

Trường hợp 1: (O) và (O’) tiếp xúc ngoài:

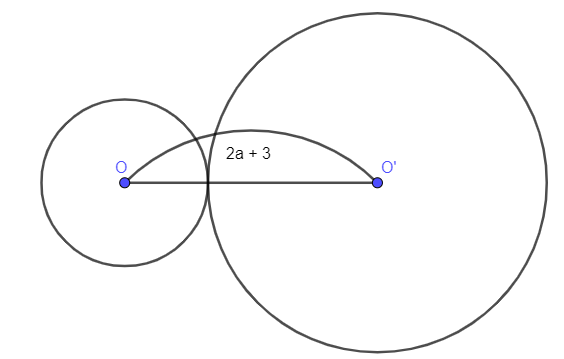
Ta có:

OO’ = r + r’ ( với r là bán kính đường tròn (O) và r’ là bán kính đường tròn (O’)).

$\iff 2a+3=4+11$

$\iff 2a+3=15$

$\iff 2a=15-3$

$\iff 2a=12$

$\iff a=6cm$

Trường hợp 2: (O) và (O’) tiếp xúc trong

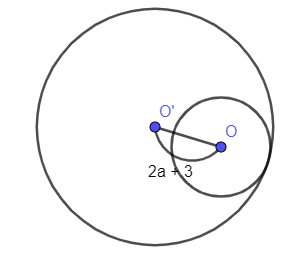
OO’ = r’ – r

$\iff 2a+3=11-4$

$\iff 2a+3=7$

$\iff 2a=7-3$

$\iff 2a=4$

$\iff a=2cm$

Vậy a = 2cm hoặc a = 6cm thì (O) và (O’) tiếp xúc.

Ví dụ 2: Cho hai đường tròn (O; 4cm) và (O’; 3cm) có OO’ = 5cm. Hai đường tròn này cắt nhau tại A và B. Tính AB.

Lời giải:

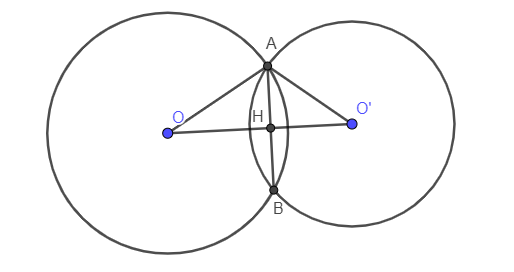
Vì A là giao của (O) và (O’) nên OA = 4cm và O’A = 3cm.

Xét tam giác OAO’ có:

$O{A}^2=4^2=16$

$O\text{'}{A}^2=3^2=9$

$O\text{}O{\text{'}}^2=5^2=25$

Vì $O\text{}O{\text{'}}^2=O{A}^2+O\text{'}{A}^2\left(25=16+9\right)$

Do đó tam giác OAO’ vuông tại A (định lý Py – ta – go đảo)

Vì OO’ cắt nhau tại A và B nên OO’ vuông góc với AB (tính chất).

Gọi giao điểm của OO’ và AB là H

Ta có OO’ là đường trung trực của AB (tính chất đường nối tâm)

Nên H là trung điểm của AB và $AB\perp O{O}^{\text{'}}$ tại H

Xét tam giác OAO’ vuông tại A đường cao AH có:

OA.O’A = AH.OO’ ( hệ thức lượng trong tam giác vuông)

$\iff$4.3 = AH.5

$\iff$5AH = 12

$\iff$AH = 12:5

$\iff$AH = 2,4cm

Vì H là trung điểm của AB nên AB = 2AH = 2.2,4 = 4,8cm.