Hệ thức giữa cạnh và đường cao trong tam giác vuông đầy đủ và cách giải - Toán lớp 9

A. Lý thuyết

Cho ∆ABC vuông tại A có : AH là đường cao. (Như hình vẽ dưới)

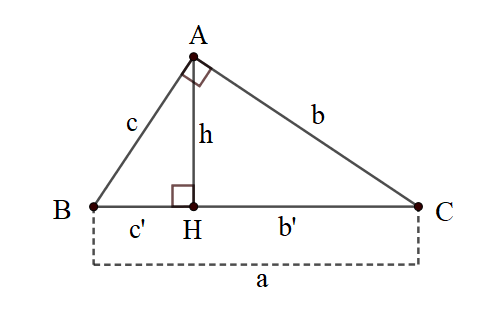
Ta có : AB = c (cạnh đối diện góc C) ; AC = b (cạnh đối diện góc B) ; BC = a (cạnh đối diện góc A) ;

AH = h (đường cao); BH = c’ (hình chiếu của c); CH = b’ (hình chiếu của b)

Khi đó, ta có các hệ thức như sau :

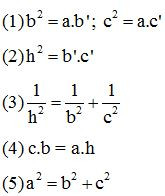
B. Phương pháp giải

Ứng dụng 5 hệ thức giữa cạnh và đường cao trong tam giác vuông trong phần lí thuyết để tìm các giá trị theo yêu cầu bài toán.

C. Ví dụ minh họa

Bài 1: Cho ∆ ABC vuông tại A có AB = 3cm, AC = 4cm. AH là đường cao. Tính BC, AH.

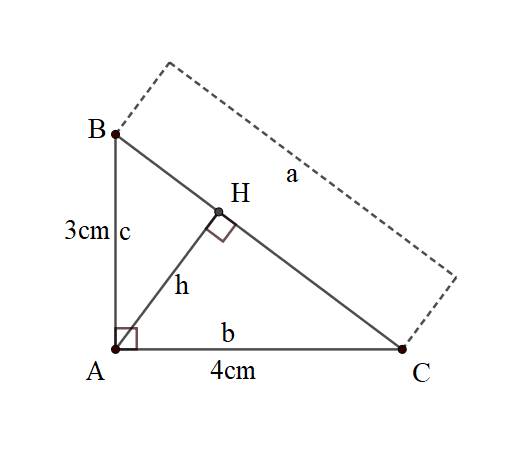
Giải:

Xét ∆ABC vuông tại A có đường cao AH:

+) Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

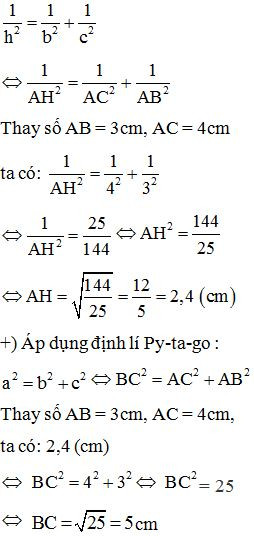
Bài 2: Cho ∆ABC vuông tại A có đường cao AH. Biết BH = 10cm, CH = 40 cm. Tính AH, AB, AC.

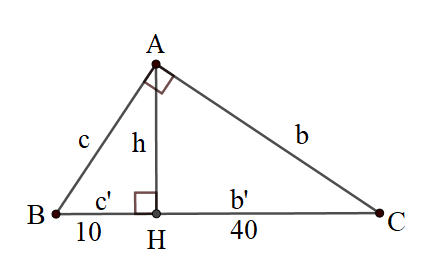
Giải:

Xét ∆ABC vuông tại A có đường cao AH:

+) Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có: $h^2=b\text{'}.c\text{'}$

$\iff$AH² = CH.BH

Thay số CH = 40cm và BH = 10cm ta có:

AH² = 40.10

AH² = 400

$\iff$AH = $\sqrt{400}$ = 20 (cm)

+) Ta lại có : BC = BH + CH = 10 + 40 = 50 (cm)

+) Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có: $b^2=a.b\text{'}$

$\iff$AC² = BC.CH

Thay số BC = 50 cm và CH = 40 cm ta có:

AC² = 50.40

AC² = 2000

AC = $\sqrt{2000}$ = 20$\sqrt{5}$ (cm)

+) Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có: $c^2=a.c\text{'}$

$\iff$AB² = BC.BH

Thay số BC = 50 cm và BH = 10 cm ta có:

AB² = 50.10

AB² = 500

AB = $\sqrt{500}$ = 10$\sqrt{5}$ (cm)

Bài 3: Tính các giá trị x, y trong hình sau:

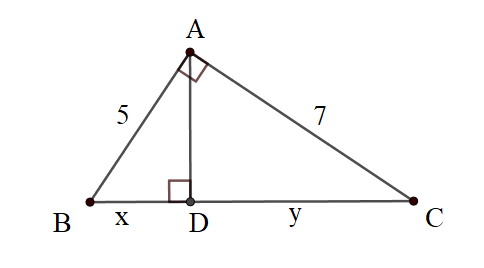
Giải :

Xét ∆ABC vuông tại A có đường cao AD:

+) Áp dụng định lí Py-ta-go :

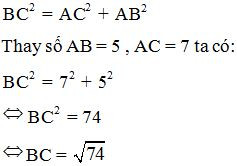
+) Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

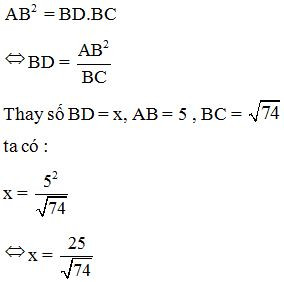
+) Mặt khác ta có:

BD + CD = BC

$\iff$CD = BC – BD

Thay số BC = $\sqrt{74}$, BD = $\frac{25}{\sqrt{74}}$, CD = y  ta có:

 y = $\sqrt{74}-\frac{25}{\sqrt{74}}=\frac{49}{\sqrt{74}}$

D. Bài tập tự luyện

Bài 1: Tính x, y trong trường hợp sau:

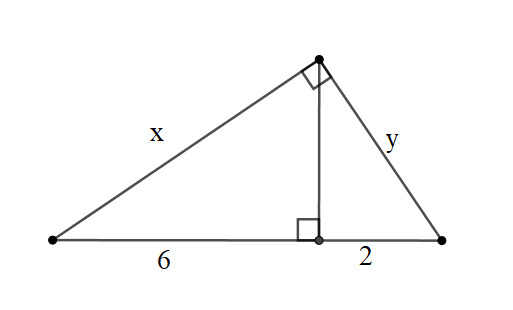
Đáp án: x = $4\sqrt{3}$, y = 4

Bài 2: Trong tam giác vuông, trong đó các cạnh góc vuông dài 6cm và 8cm. Tính độ dài đường cao xuất phát từ đỉnh góc vuông và độ dài hình chiếu của các cạnh góc vuông lên cạnh huyền.

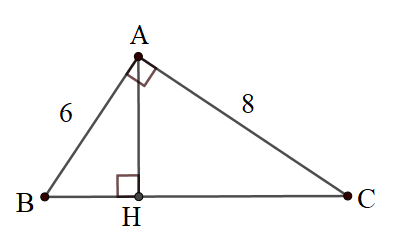
Đáp án: AH = 4,8 cm ; BH = 3,6 cm ; CH = 6,4 cm

Bài 3: Tính x, y trong trường hợp sau:

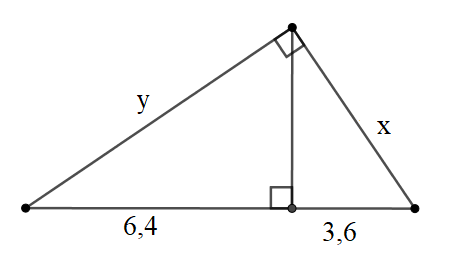
Đáp án: x = 6 ; y = 8

Bài 4: Đáp án nào sau đây là đúng ? (dựa vào hình vẽ)

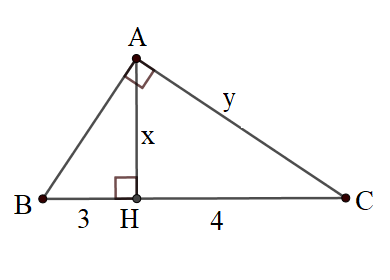
A. $x^2+y^2=12$

B. x.y = 4

C. x = $2\sqrt{3}$

D. x – y = 3

Đáp án: C

Bài 5: Cho tam giác ABC vuông tại A. AH là đường cao. Hệ thức nào sau đây là đúng ?

A. AH.BC = AB.AC

B. CH.CH = AB.AC

C. $A{H}^2=AB.AC$

D. BC = AB + AC

Đáp án: A

Bài 6: Cho ∆ ABC vuông tại A có đường cao AH=12cm, Biết BH - CH=7cm. Tính độ dài cạnh BC

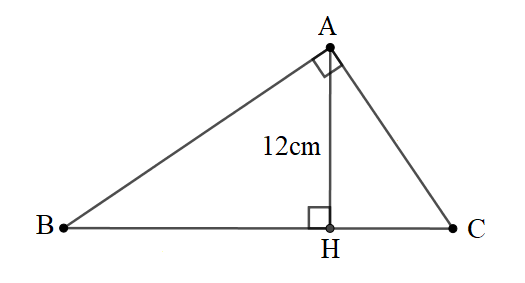
Đáp án: BC = 25cm

Bài 7: Tam giác ABC vuông tại A có AB=AC. Biết đường cao AH=4. Tính AB, AC

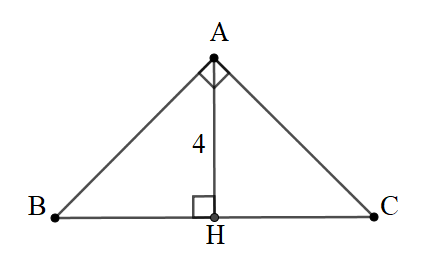
Đáp án: AB = AC = $4\sqrt{2}$

Bài 8: Cho tam giác ABC vuông tại A. Có đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21cm . Tính AH, BH, CH.

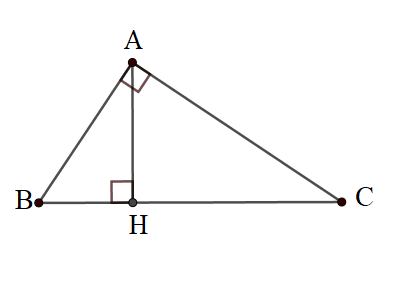
Đáp án: AH = 7,2 cm ; BH = 5,4cm; CH = 9,6cm

Bài 9: Cho hình vuông ABCD cạnh a. Biết đường chéo AC = 4cm. Tính độ dài cạnh a của hình vuông.

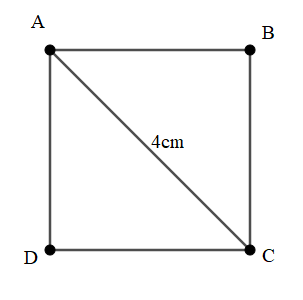
Đáp án: $a=2\sqrt{2}$(cm)

Bài 10: Cho hình chữ nhật ABCD. Kẻ AH vuông góc với đường chéo BD. Biết AH = 4cm, HD = 5cm. Tính độ dài cạnh AB,AD.

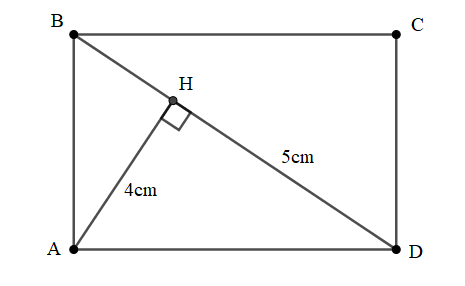
Đáp án: $AB=\frac{4\sqrt{41}}{5}\left(cm\right);$ $AC=\sqrt{41}\left(cm\right)$