Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết - Toán lớp 9

I. Lý thuyết

• Nếu hai tuyến tuyến của một đường tròn cắt nhau tại một điểm thì

- Điểm đó cách đều hai tiếp điểm.

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua hai tiếp điểm.

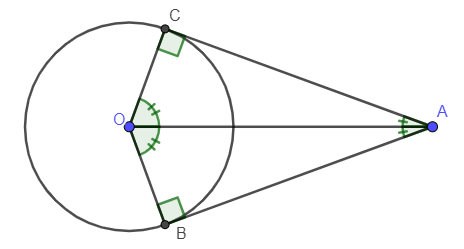
Cho đường tròn (O;R) có AB; AC là hai tiếp tuyến của đường tròn; B, C là hai tiếp điểm

Khi đó ta có:

+ AB = AC.

+ AO là tia phân giác $\widehat{BAC}$  hay $\widehat{CAO}=\widehat{BAO}=\frac{1}{2}\widehat{BAC}$ .

+ OA là tia phân giác $\widehat{BOC}$  hay $\widehat{BOA}=\widehat{COA}=\frac{1}{2}\widehat{BOC}$ .

II. Một số ví dụ

Ví dụ 1: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là tiếp điểm).

a) Chứng minh AO vuông góc với MN.

b) Vẽ đường kính NOC. Chứng minh MC // AO.

c) Tính độ dài các cạnh tam giác AMN biết: OM = 3cm, OA = 5cm.

Lời giải:

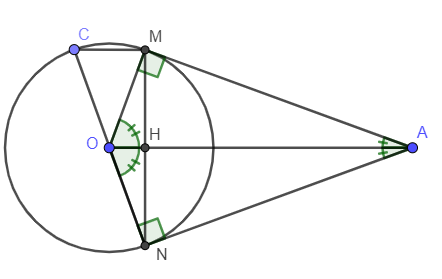
a) Gọi H là giao điểm của AO và MN.

Vì AM và AN là hai tiếp tuyến cắt nhau tại A nên OA là tia phân giác $\widehat{MON}$

$\Rightarrow \widehat{MOA}=\widehat{NOA}$ (tính chất)

Xét tam giác OMH và tam giác ONH có:

OM = ON = R

OH chung

$\widehat{MOA}=\widehat{NOA}$ (chứng minh trên)

Do đó: $\Delta OMH=\Delta ONH$ (c – g – c)

$\Rightarrow \widehat{OHM}=\widehat{OHN}$ (hai góc tương ứng)

Mà $\widehat{OHM}+\widehat{OHN}=180°$  (hai góc kề bù)

Do đó: $\widehat{OHM}=\widehat{OHN}=90°$  hay $OH\perp MN$

$\Rightarrow OA\perp MN$ (do H nằm trên OA)

b) Xét tam giác MNC có ba đỉnh M, N, C cùng nằm trên đường tròn (O)

Lại có NC là đường kính

Do đó tam giác MNC vuông tại M.

$\Rightarrow MC\perp MN$

Ta có:

$\left\{\begin{array}{l}MC\perp MN\\ OA\perp MN\end{array}\right.\Rightarrow MC//OA$ (quan hệ từ vuông góc đến song song)

c) Xét tam giác OMA vuông tại M (do AM là tiếp tuyến của (O) với M là tiếp điểm) ta có:

$O{M}^2+M{A}^2=O{A}^2$ (định lý Py – ta – go)

$\iff 3^2+M{A}^2=5^2$

$\iff M{A}^2=25-9$

$\iff M{A}^2=16$

$\iff MA=4cm$

Mà MA và NA là hai tiếp tuyến cắt nhau

$\Rightarrow MA=NA=4cm$ (tính chất)

Tam giác OAM vuông tại M, đường cao MH ta có:

MA.MO = MH.OA

$\iff 4.3=MH.5$

$\iff 5MH=12$

$\iff MH=12:5$

$\iff MH=2,4cm$

Tam giác OMN có:

OM = ON

Do đó tam giác OMN cân tại O.

$\Rightarrow$Khi đó OH vừa là đường cao vừa là đường trung tuyến.

Suy ra H là trung điểm của MN

MN = 2MH = 2,4.2 = 4,8cm

Vậy tam giác AMN có AM = AN = 4 cm, MN = 4,8 cm.

Ví dụ 2: Từ điểm A nằm ngoài đường tròn (O; R) kẻ hai tiếp tuyến AB, AC (với B và C là hai tiếp điểm). Kẻ BE vuông góc với AC, CF vuông góc với AB (E thuộc AC, F thuộc AB), BE và CF cắt nhau tại H.

a) Chứng minh tứ giác OBHC là hình thoi.

b) Chứng minh ba điểm A, H, O thẳng hàng.

Lời giải:

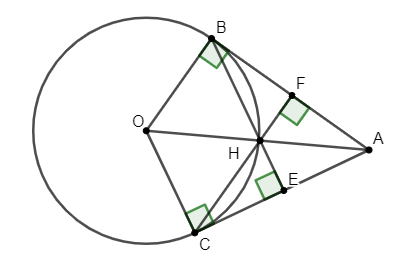
a) Vì AB là tiếp tuyến của đường tròn (O) tại B nên OB$\perp$ AB

Lại có CF $\perp$ AB (giải thuyết)

Do đó: OB // CF hay OB // CH   (1)

Vì AC là tiếp tuyến của đường tròn (O) tại C nên OC $\perp$ AC

Lại có: BE $\perp$ AC (giả thuyết)

Do đó: OC // BE hay OC // BH   (2)

Xét tứ giác OBHC có:

OB // CH (theo (1))

OC // BH (theo (2))

Do đó tứ giác OBHC là hình bình hành (dấu hiệu nhận biết)

Lại có: OB = OC nên hình bình hành OBHC là hình thoi (dấu hiệu nhận biết).

b) Vì OBHC là hình thoi nên OH là đường phân giác góc $\widehat{BOC}$  (tính chất) (3)

Do AB, AC là hai tiếp tuyến của đường tròn (O) và chúng cắt nhau tại A

Nên OA là đường phân giác góc (tính chất) $\widehat{BOC}$  (4)

Từ (3) và (4)$\Rightarrow OA\equiv OH$ hay O, A, H thẳng hàng.