(2023) Đề thi thử Vật Lí Sở Quảng Bình có đáp án
-
277 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
Phát biểu nào sau đây là sai khi nói về ánh sáng đơn sắc?
 Xem đáp án
Xem đáp án
Chiết suất của một môi trường trong suốt đối với ánh sáng đỏ nhỏ hơn chiết suất của môi trường đó đối với ánh sáng tím. Chọn C
Câu 4:
Trong sóng cơ, sóng dọc là sóng mà phương dao động của các phần tử môi trường
 Xem đáp án
Xem đáp án
Chọn A
Câu 5:
Mạch điện kín gồm một nguồn điện có suất điện động và điện trở trong , điện trở mạch ngoài là . Cường độ dòng điện trong mạch là
 Xem đáp án
Xem đáp án
Chọn C
Câu 6:
Đặt vào hai đầu cuộn cảm điện áp xoay chiều có tần số góc . Cảm kháng của cuộn cảm là
 Xem đáp án
Xem đáp án
\({Z_L} = \omega L\). Chọn C
Câu 8:
Trong sơ đồ khối của một máy thu thanh đơn giản không có bộ phận nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn C
Câu 11:
Một con lắc đơn chiều dài l đang dao động điều hòa. Li độ cong s và li độ góc liên hệ với nhau bằng biểu thức nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
Câu 13:
Một máy phát điện xoay chiều một pha có p cặp cực, rôto quay với tốc độ n vòng/giây. Từ thông qua mỗi cuộn dây của stato biến thiên tuần hoàn với tần số
 Xem đáp án
Xem đáp án
Chọn C
Câu 15:
 Xem đáp án
Xem đáp án
Chọn B
Câu 16:
 Xem đáp án
Xem đáp án
Chọn A
Câu 17:
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số, có phương trình dao động 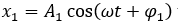 và
và 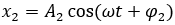 . Dao động tổng hợp có phương trình
. Dao động tổng hợp có phương trình 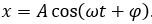 . Biểu thức nào sau đây đúng?
. Biểu thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn B
Câu 18:
 Xem đáp án
Xem đáp án
Chọn A
Câu 19:
Cho mạch điện xoay chiểu gồm R, L, C
mắc nối tiếp, cường độ dòng điện trong mạch là i = I0cos và điện áp giữa hai đầu mạch là . Công suất tiêu thụ của mạch được tính theo biểu thức nào sau đây?
 Xem đáp án
Xem đáp án
\(P = UI\cos \varphi \). Chọn B
Câu 20:
Một con lắc lò xo có độ cứng k và khối lượng m. Đại lượng 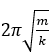 là
là
 Xem đáp án
Xem đáp án
\(T = 2\pi \sqrt {\frac{m}{k}} \). Chọn D
Câu 21:
Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc. Khoảng vân giao thoa trên màn quan sát là i. Khoảng cách giữa 4 vân sáng liên tiếp là
 Xem đáp án
Xem đáp án
Chọn C
Câu 22:
Trên một sợi dây đàn hồi dài 1,2 m với hai đầu cố định, đang có sóng dừng. Biết sóng truyền trên dây có tần số 100 Hz và tốc độ 80 m/s. Số bụng sóng trên dây là
 Xem đáp án
Xem đáp án
\(\lambda = \frac{v}{f} = \frac{{80}}{{100}} = 0,8m\)
\(l = k.\frac{\lambda }{2} \Rightarrow 1,2 = k.\frac{{0,8}}{2} \Rightarrow k = 3\). Chọn A
Câu 23:
 Xem đáp án
Xem đáp án
\(\Delta m = 8{m_p} + 8{m_n} - {m_O} = 8.1,0073 + 8.1,0087 - 15,9904 = 0,1376\)
\({W_{lk}} = \Delta m{c^2} = 0,1376.931,5 \approx 128,17MeV\). Chọn B
Câu 24:
Giới hạn quang điện của một kim loại là 0,30 mm. Công thoát của êlectron khỏi kim loại này là
 Xem đáp án
Xem đáp án
\(\varepsilon = \frac{{hc}}{\lambda } = \frac{{1,{{9875.10}^{ - 25}}}}{{0,{{3.10}^{ - 6}}}} = 6,{625.10^{ - 19}}J\). Chọn B
Câu 25:
Một vòng dây dẫn hình tròn bán kính 50 cm có dòng điện cường độ 2 \[A.\] Cảm ứng từ tại tâm vòng dây có độ lớn là
 Xem đáp án
Xem đáp án
\(B = 2\pi .1{\not 0^{ - 7}}.\frac{I}{R} = 2\pi .1{\not 0^{ - 7}}.\frac{2}{{0,5}} \approx 2,{5.10^{ - 6}}T\). Chọn D
Câu 26:
 Xem đáp án
Xem đáp án
\(l = n.\frac{\lambda }{2} = n.\frac{{vT}}{2} \Rightarrow T = \frac{{2l}}{{nv}}\). Chọn A
Câu 27:
Tại một vị trí trên Trái đất, con lắc đơn có chiều dài l1 dao động điều hòa với chu kì T1. con lắc đơn có chiều dài l2 (l2 < l1) dao động điều hòa với chu kì T2. Cũng tại vị trí đó, con lắc đơn có chiều dài (l1 - l2) dao động điều hòa với chu kì là
 Xem đáp án
Xem đáp án
. Chọn A
Câu 28:
 Xem đáp án
Xem đáp án
. Chọn C
Câu 29:
Theo mấu nguyên tử Bo, nguyên tử hiđrô chuyển từ trạng thái dừng có năng lượng En = -1,5eV sang trạng thái dừng có năng lượng Em = -3,4eV. Bước sóng của bức xạ mà nguyên tử hiđrô phát ra bằng
 Xem đáp án
Xem đáp án
\(\frac{{hc}}{\lambda } = {E_n} - {E_m} \Rightarrow \frac{{1,{{9875.10}^{ - 25}}}}{\lambda } = \left( { - 1,5 + 3,4} \right).1,{6.10^{ - 19}} \Rightarrow \lambda \approx 0,{654.10^{ - 6}}m\). Chọn D
Câu 30:
Đặt điện áp vào hai đầu một tụ điện có điện dung F. Dung kháng của tụ điện là
 Xem đáp án
Xem đáp án
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \). Chọn D
Câu 31:
Cho mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Trong đó điện trở R=100 Ω , độ tự cảm L của cuộn dây cảm thuần và điện dung C của tụ điện không đổi. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số góc ω có thể thay đổi được. Khi thì tổng trở của mạch là 120 Ω . Tăng tần số góc từ giá trị thêm 500 (rad/s) thì tổng trở của mạch lại có giá trị 120 Ω. Giá trị của L là
 Xem đáp án
Xem đáp án
\(\omega \) thay đổi cho cùng \(Z \Rightarrow {Z^2} = {R^2} + {\left( {{Z_{L1}} - {Z_{L2}}} \right)^2} = {R^2} + {L^2}{\left( {{\omega _1} - {\omega _2}} \right)^2}\)
\( \Rightarrow {120^2} = {100^2} + {L^2}.{\left( {500\pi } \right)^2} \Rightarrow L \approx 42,{2.10^{ - 3}}H = 42,2mH\). Chọn B
Câu 32:
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại hai điểm A và B dao động cùng pha theo phương thẳng đứng với tần số f = 20Hz. Tốc độ truyền sóng trên mặt chất lỏng là v = 60 cm/s, khoảng cách giữa hai điểm A và B là 16 cm. Điểm M thuộc đoạn thẳng AB và cách A một khoảng 9 cm. Đường tròn (C) có tâm là M và bán kính 5 cm trên mặt chất lỏng. Số điểm giao thoa cực đại trên đường tròn (C) là
 Xem đáp án
Xem đáp án
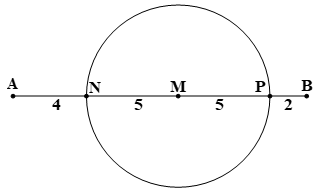
\(\lambda = \frac{v}{f} = \frac{{60}}{{20}} = 3cm\)
\({k_N} = \frac{{NA - NB}}{\lambda } = \frac{{4 - 12}}{3} \approx - 2,7\) và \({k_P} = \frac{{PA - PB}}{\lambda } = \frac{{14 - 2}}{3} = 4\)
Cực đại bậc \( - 2\) đến 3 cắt đường tròn tại 2 điểm, còn cực đại bậc 4 tiếp xúc đường tròn \( \Rightarrow \)trên đường tròn có \(6.2 + 1 = 13\) cực đại. Chọn A
Câu 33:
Một tấm ván đồng chất chiều dài l = 20 cm, khối lượng M = 1,2 kg được đặt trên mặt bàn nằm ngang vuông góc với mép bàn, đầu A nằm trên mặt bàn, đầu B nhô ra khỏi mép bàn một đoạn BC = 40 cm. Hai con lắc lò xo có các lò xo cùng độ cứng k = 15 N/m gắn với các quả cầu nhỏ cùng khối lượng m = 0,8 kg. Một con lắc được treo thẳng đứng, điểm treo tại đầu B của tấm ván. Con lắc còn lại đặt nằm ngang dọc theo tấm ván, một đầu lò xo này gắn vào một chốt cố định trên mặt bàn, vị trí cân bằng của quả cầu trên ván cách mép bàn C một khoảng 20 .
Hệ được biểu diễn bằng hình vẽ bên. Bỏ qua ma sát và lấy g = 10 m/s2. Đẩy quả cầu trên ván dọc theo trục lò xo để lò xo nén . Nâng quả cầu bên dưới từ vị trí cân bằng lên một khoảng 16 . Thả nhẹ quả cầu bên trên trước, khi nó đến vị trí cân bằng thì thả quả cầu bên dưới. Để tấm ván không bị nghiêng, trong mỗi chu kì dao động của các con lắc, phải giữ tấm ván trong trong thời gian nhỏ nhất là
 Xem đáp án
Xem đáp án
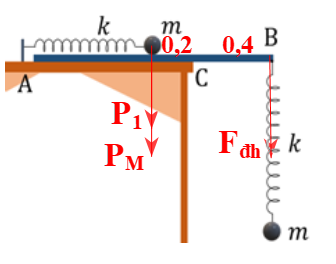
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{15}}{{0,8}}} = 2,5\sqrt 3 \) (rad/s)
\(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,8.10}}{{15}} = \frac{8}{{15}}m > A = 0,16m\)
\( \to \)lò xo luôn dãn \( \to {F_{dh}}\) tác dụng vào B luôn hướng xuống
Để ván bị nghiêng thì theo quy tắc momen lực đối với C có
\(k\left( {\Delta {l_0} + {x_2}} \right).BC > M.g.0,2 + {m_1}.g.\left( {0,2 - {x_1}} \right)\)
\( \Rightarrow 15.\left( {\frac{8}{{15}} + 0,16\cos \left( {2,5\sqrt 3 t + \pi } \right)} \right).0,4 \ge 1,2.10.0,2 + 0,8.10.\left[ {0,2 - 0,16\cos \left( {2,5\sqrt 3 t - \frac{\pi }{2}} \right)} \right]\)
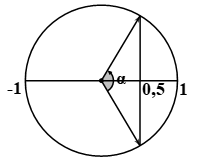
\( \Rightarrow 1,6\cos \left( {2,5\sqrt 3 t - 2,2143} \right) \ge 0,8 \Rightarrow \cos \left( {2,5\sqrt 3 t - 2,2143} \right) \ge \frac{1}{2}\)
Trong 1 chu kì thời gian ván nghiêng là \(\Delta t = \frac{\alpha }{\omega } = \frac{{2\pi /3}}{{2,5\sqrt 3 }} \approx 0,48s\). Chọn C
Câu 34:
Đặt điện áp xoay chiều 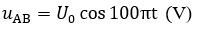 (U0 không đổi) vào hai đầu một đoạn mạch AB như hình vẽ. Trong mạch, R1 là biến trở, cuộn dây cảm thuần có độ tự cảm L thay đổi được,
(U0 không đổi) vào hai đầu một đoạn mạch AB như hình vẽ. Trong mạch, R1 là biến trở, cuộn dây cảm thuần có độ tự cảm L thay đổi được, 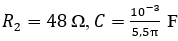 . Điều chỉnh R1 và L sao cho điện áp hiệu dụng trên đoạn AM luôn gấp hai lần điện áp hiệu dụng trên MB. Độ lệch pha giữa các điện áp uAM và uAB là . Khi đạt cực đại thì tổng trở của mạch AB là
. Điều chỉnh R1 và L sao cho điện áp hiệu dụng trên đoạn AM luôn gấp hai lần điện áp hiệu dụng trên MB. Độ lệch pha giữa các điện áp uAM và uAB là . Khi đạt cực đại thì tổng trở của mạch AB là
 Xem đáp án
Xem đáp án
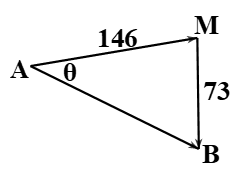
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 3}}}}{{5,5\pi }}}} = 55\Omega \)
\[{Z_{MB}} = \sqrt {R_2^2 + Z_C^2} = 2\sqrt {{{48}^2} + {{55}^2}} = 73\Omega \]
\({U_{AM}} = 2{U_{MB}} \Rightarrow {Z_{AM}} = 2{Z_{MB}} = 2.73 = 146\Omega \)
\(\cos \theta = \frac{{Z_{AM}^2 + {Z^2} - Z_{MB}^2}}{{2{Z_{AM}}Z}} = \frac{{{{146}^2} + {Z^2} - {{73}^2}}}{{2.146.Z}} = \frac{{\frac{{15987}}{Z} + Z}}{{2.146}} \ge \frac{{2\sqrt {15987} }}{{2.146}} \Rightarrow \theta \le \frac{\pi }{6}\)
Dấu = xảy ra \( \Leftrightarrow \frac{{15987}}{Z} = Z \Leftrightarrow Z \approx 126,44\Omega \). Chọn D
Câu 35:
Theo mẫu nguyên tử Bo, năng lượng của nguyên tử hiđrô ở các trạng thái dừng K; L; M; N; O; P;... lần lượt là EK = -13,6 eV; EL = -,40 eV; EM = -1,51 eV; EN = -0,85 eV; EO = -0,54 eV; EP = -0,38 eV;... Một khối khí hiđrô được kích thích để phát ra ánh sáng. Ánh sáng phát ra từ khối khí hiđrô này là ánh sáng tổng hợp gồm 6 bức xạ khác nhau. Trong 6 bức xạ đó có n bức xạ có thể gây ra hiện tượng quang điện đối với canxi (có giới hạn quang điện 0,43). Giá trị của n là
 Xem đáp án
Xem đáp án
\(\frac{{n\left( {n - 1} \right)}}{2} = 6 \Rightarrow n = 4 \to \)khối khí được kích thích lên quỹ đạo N
\(A = \frac{{hc}}{\lambda } = \frac{{1,{{9875.10}^{ - 25}}}}{{0,{{43.10}^{ - 6}}.1,{{6.10}^{ - 19}}}} \approx 2,89eV\)
Từ \(N,M,L \to K\) phát ra \(\varepsilon > 2,89eV\) là có 3 vạch. Chọn B
Câu 36:
Chuỗi phóng xạ của urani kết thúc là sản phẩm chì bền, vói chu kì bán rã 4,5.109 năm. Chuỗi phóng xạ của urani kết thúc là sản phẩm chì bền với chu kì bán rã 0,71.109 năm. Người ta cho rằng, khi Trái đất hình thành, đã có mặt của đồng vị chì và urani nhưng chưa có sản phẩm phân rã của chúng. Một mâu quặng tigm thấy có lẫn chì và urani, trong đó tỉ lệ số nguyên tử của hai đồng vị chì , tương ứng là 1,00:29,6:22,6; ti lệ số nguyên tử của hai đồng vị unrani tương ứng là 1:137. Trong đó đồng vị chỉ được dùng để tham khảo vì nó không có nguồn gốc phóng xạ. Một mẫu quặng khác chỉ có chì tinh khiết cho tỉ lệ tương tự 1,00:17,9:15,5, đây được xem là tỉ lệ chì khi Trái đất hình thành. Với những số liệu đã cho, có thể tính được tuổi của Trái đất là
 Xem đáp án
Xem đáp án
\(\frac{{\Delta N}}{N} = \frac{{1 - {2^{\frac{{ - t}}{T}}}}}{{{2^{\frac{{ - t}}{T}}}}} = {2^{\frac{t}{T}}} - 1 \Rightarrow \frac{{\Delta {N_1}}}{{\Delta {N_2}}}.\frac{{{N_2}}}{{{N_1}}} = \frac{{{2^{\frac{t}{{{T_1}}}}} - 1}}{{{2^{\frac{t}{{{T_2}}}}} - 1}} \Rightarrow \frac{{29,6 - 17,9}}{{22,6 - 15,5}}.\frac{1}{{137}} = \frac{{{2^{\frac{t}{{4,5}}}} - 1}}{{{2^{\frac{t}{{0,71}}}} - 1}} \Rightarrow t \approx 4,558\). Chọn A
Cách 2:
* Sơ đồ phân rã: (chu kì T1 = 4,5.109 năm)
và (chu kì T2 = 0,71.109 năm).
* Khi mới hình thành (tại thời điểm t = 0): \(\left\{ \begin{array}{l}{N_{Pb206}} = 17,9a\\{N_{Pb207}} = 15,5a\end{array} \right.\)
* Khi tìm thấy ở hiện tại (tại thời điểm t): \(\left\{ \begin{array}{l}{N_{Pb206}} = 29,5a\\{N_{Pb207}} = 22,6a\end{array} \right.\)
* Số hạt nhân chì tăng thêm = số hạt nhân urani bị phân rã ⟹
\(\left\{ \begin{array}{l}\Delta {N_{U238}} = \Delta {N_{Pb206}} = 29,5a - 17,9a = 11,6a\\\Delta {N_{U235}} = \Delta {N_{Pb207}} = 22,6a - 15,5a = 7,1a\end{array} \right.\)
* Tỉ lệ số hạt nhân urani bị phân rã: \(\frac{{\Delta {N_{U238}}}}{{\Delta {N_{U235}}}} = \frac{{{N_{01}}.(1 - {2^{ - \frac{t}{{{T_1}}}}})}}{{{N_{02}}.(1 - {2^{ - \frac{t}{{{T_2}}}}})}} = \frac{{11,6a}}{{7,1a}} = \frac{{116}}{{71}}\) (1).
* Tại thời điểm t, tỉ lệ số hạt nhân urani còn lại: \(\frac{{{N_{U238}}}}{{{N_{U235}}}} = \frac{{{N_{01}}{{.2}^{ - \frac{t}{{{T_1}}}}}}}{{{N_{02}}{{.2}^{ - \frac{t}{{{T_2}}}}}}} = \frac{{{N_{01}}}}{{{N_{02}}}}{.2^{ - t.\left( {\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}} \right)}} = 138\) (2).
* Lấy \(\frac{{(1)}}{{(2)}} \Rightarrow \frac{{(1 - {2^{ - \frac{t}{{{T_1}}}}})}}{{(1 - {2^{ - \frac{t}{{{T_2}}}}})}} \times {2^{t.\left( {\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}} \right)}} = \frac{{116}}{{71 \times 138}}\) ⟹ t = 4,582.109 năm.
Chọn A
Câu 37:
Một sợi dây dài 1,8 m được cắt làm hai đoạn, mỗi đoạn dây được gắn với một quả cầu nhỏ tạo thành con lắc đơn. Hai con lắc đơn này có điểm treo gần nhau và ở cùng độ cao. Kéo nhẹ các quả cầu để các sợi dây lệch khỏi vị trí cân bằng các góc bằng nhau và bằng đồng thời các sợi dây song song với nhau. Thả nhẹ hai con lắc ở cùng một thời điểm để chúng dao động điều hòa trong hai mặt phẳng thẳng đứng song song với nhau. Khi một trong hai con lắc lệch góc so với vị trí cân bằng của nó lần thứ hai thì hai sợi dây lại song song với nhau. Chiều dài của một trong hai đoạn dây là
 Xem đáp án
Xem đáp án
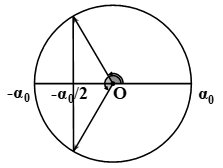
* Theo giả thiết: t = \(\frac{{{T_1}}}{4} + \frac{{{T_1}}}{{12}} = \frac{{{T_2}}}{2} + \frac{{{T_2}}}{6}\) ⟹ \(\frac{{{T_1}}}{{{T_2}}} = 2 = \sqrt {\frac{{{\ell _1}}}{{{\ell _2}}}} \) ⟹ ℓ1 = 4ℓ2 (1).
Giải thích: Con lắc 1 đi từ: \(\alpha = {\alpha _0} \to \alpha = 0 \to \alpha = - \frac{{{\alpha _0}}}{2}\).
Con lắc 2 đi từ: \(\alpha = {\alpha _0} \to \alpha = - {\alpha _0} \to \alpha = - \frac{{{\alpha _0}}}{2}\).
* Mặt khác: ℓ1 + ℓ2 = 1,8 m.
* Từ (1) và (2) ⟹ ℓ1 = 1,44 m và ℓ2 = 0,36 m.
Chọn D
Câu 38:
Cho mạch điện xoay chiều gồm R, L, C mắc nối tiếp như hình vẽ bên (hình H.1). Hình H.2 là các đồ thị biểu diễn sự phụ thuộc của điện áp uAM giữa hai điểm A, M và điện áp uAB giữa hai điểm M, B trong mạch theo thời gian t. Tại thời điểm điện áp tức thời hai đầu đoạn mạch AB có giá trị 165 V. Biểu thức của điện áp hai đầu đoạn mạch AB tính theo t (t tính bằng s) là
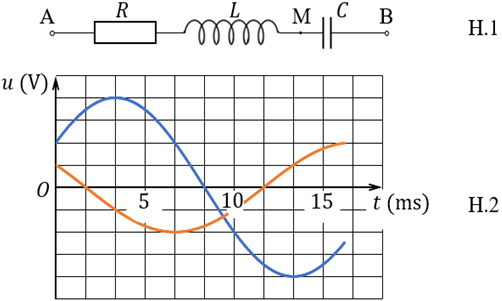
 Xem đáp án
Xem đáp án
Tại thời điểm \(t = \frac{{10}}{3}ms\) thì \({u_{AM}} + {u_{MB}} = {u_{AB}} \Rightarrow - 1\^o + 4\^o = 165V \Rightarrow 1\^o = 55V\)
\({u_{AB}} = {u_{AM}} + {u_{MB}} = 2.55\angle \frac{\pi }{3} + 4.55\angle - \frac{\pi }{3} = 110\sqrt 3 \angle - \frac{\pi }{6}\). Chọn C
Cách 2:
Trên trục tung Ou: 2 ô = U ; Trên trục hoanh Ot : 6 ô = 10 ms ;
uMB có biên độ 4 ô = 2U và chậm pha hơn uAM có biên độ 2 ô= U.
1 Chu kì 12 ô = 2 . 6 ô =2. 10 ms =0,02s => ω =100π rad/s
Theo đồ thị ta có: \[{u_{MB}} = 2Uc{\rm{os}}(100\pi t - \frac{\pi }{3})V;{u_{AM}} = Uc{\rm{os}}(100\pi t + \frac{\pi }{3})V;\]
Tại t= 10/3 s =2 ô: \[u = {u_{AM}} + {u_{MB}} = 2U + ( - \frac{U}{2}) = 165V = > U = 110V\].
\[\begin{array}{l}{u_{AB}} = {u_{MB}} + {u_{AM}} = 2Uc{\rm{os}}(100\pi t - \frac{\pi }{3})V + Uc{\rm{os}}(100\pi t + \frac{\pi }{3})V;\\{u_{AB}} = 220c{\rm{os}}(100\pi t - \frac{\pi }{3})V + 110c{\rm{os}}(100\pi t + \frac{\pi }{3})V\\{u_{AB}} = 110\sqrt 3 c{\rm{os}}(100\pi t - \frac{\pi }{6})V\end{array}\]
Chọn C
Câu 39:
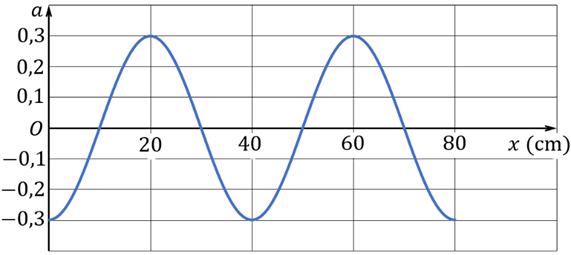
Trên một sợi dây đang có sóng dừng, hai đầu sợi dây đều là nút sóng. Chọn trục Ox trùng với đường thẳng chứa sợi dây khi nó duỗi thẳng, gốc O tại một đầu sợi dây. Xét sợi dây khi nó biến dạng nhiều nhất. Gọi hệ số góc của tiếp tuyến với sợi dây tại điểm có tọa độ x là . Sự phụ thuộc của theo x được biểu diễn bằng đồ thị như hình vẽ bên. Khoảng cách lớn nhất giữa hai bụng sóng là
 Xem đáp án
Xem đáp án
\(u = {A_b}\sin \left( {\frac{{2\pi x}}{\lambda }} \right) \Rightarrow \alpha = u' = {A_b}.\frac{{2\pi }}{\lambda }\cos \left( {\frac{{2\pi x}}{\lambda }} \right)\)
\({\alpha _{\max }} = {A_b}.\frac{{2\pi }}{\lambda } \Rightarrow 0,3 = {A_b}.\frac{{2\pi }}{{40}} \Rightarrow {A_b} = \frac{6}{\pi }cm\)
\({d_{\max }} = \sqrt {{{\left( {l - 2.\frac{\lambda }{4}} \right)}^2} + {{\left( {2{A_b}} \right)}^2}} = \sqrt {{{\left( {80 - 2.\frac{{40}}{4}} \right)}^2} + {{\left( {2.\frac{6}{\pi }} \right)}^2}} \approx 60,12cm\). Chọn B
Câu 40:
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5 mm, màn quan sát cách mặt phẳng chứa hai khe một khoảng 1,5 m. Chiếu sáng hai khe bằng ánh sáng tổng hợp gồm hai bức xạ có bước sóng
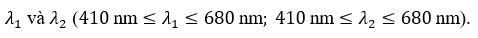
Trên màn quan sát người ta đánh dấu một điểm M cách vân sáng trung tâm một khoảng 12,6 mm. Tại M có vân sáng của bức xạ bước sóng 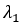 và vân tối của bức xạ bước sóng
và vân tối của bức xạ bước sóng 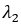 . Giữa M và vân sáng trung tâm có hai vị trí mà tại đó vân sáng của hai bức xạ trùng nhau. Để tại M chỉ có vân sáng của một bức xạ
. Giữa M và vân sáng trung tâm có hai vị trí mà tại đó vân sáng của hai bức xạ trùng nhau. Để tại M chỉ có vân sáng của một bức xạ 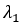 , phải dịch chuyển màn tịnh tiến theo phương vuông góc với màn, ra xa nguồn sáng thêm một khoảng nhỏ nhất bằng . Bước sóng của hai bức xạ
, phải dịch chuyển màn tịnh tiến theo phương vuông góc với màn, ra xa nguồn sáng thêm một khoảng nhỏ nhất bằng . Bước sóng của hai bức xạ 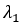 và
và 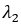 chênh lệch nhau
chênh lệch nhau
 Xem đáp án
Xem đáp án
\({x_M} = {k_{12}}.\frac{{{\lambda _{12}}D}}{a} = {k_1}.\frac{{{\lambda _2}D}}{a} = {k_2}.\frac{{{\lambda _2}D}}{a}\)
\( \Rightarrow 12,6 = 2,5.\frac{{{\lambda _{12}}.1,5}}{{0,5}} = {k_1}.\frac{{{\lambda _1}.1,5}}{{0,5}} = \left( {{k_1} - 1} \right).\frac{{{\lambda _2}.\left( {1,5 + \frac{1}{6}} \right)}}{{0,5}} = {k_2}.\frac{{{\lambda _2}.1,5}}{{0,5}} \Rightarrow \left\{ \begin{array}{l}{k_1} = 10\\{\lambda _1} = 0,42\mu m\\{\lambda _{12}} = 1,68\mu m\end{array} \right.\)
với \({k_2}\) bán nguyên
Lại có \(2,5{\lambda _{12}} = {k_2}{\lambda _2} \Rightarrow {\lambda _{12}} = \frac{{{k_2}}}{{2,5}}{\lambda _2} \Rightarrow \)\(\frac{{{k_2}}}{{2,5}}\) là số nguyên \( \Rightarrow {k_2} = 7,5 \Rightarrow {\lambda _2} = 0,56\mu m\)
Vậy \({\lambda _2} - {\lambda _1} = 0,56 - 0,42 = 0,14\mu m = 140nm\). Chọn C
Cách 2:
Hướng dẫn
* Giả sử l1 < l2.
* Lúc đầu, tại M là vị trí vân sáng của l1 trùng với vị trí vân tối của l2.
⟹ xM = k1.\(\frac{{{\lambda _1}D}}{a}\)= (k2 - 0,5).\(\frac{{{\lambda _2}D}}{a}\) (1) (lưu ý: \(\frac{{{\lambda _1}}}{{{\lambda _2}}}\) tối giản = \(\frac{{l\^I }}{{ch\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/
\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} n}}\) hoặc \(\frac{{ch\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/
\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} n}}{{l\^I }}\)).
* Lúc sau: D’ = \(D + \frac{1}{6}\) (m), chỉ có vân sáng của một bức xạ.
⟹ xM = (k1 - 1).\(\frac{{{\lambda _1}.(D + \frac{1}{6})}}{a}\) (2).
* Từ (1) và (2) ⟹ k1.D = (k1 - 1).(\(D + \frac{1}{6}\)) ⟹ k1 = 10 ⟹ l1 = \(\frac{{a.{x_M}}}{{{k_1}.D}}\)= 0,42 mm = 420 nm.
* Giữa M và vân sáng trung tâm có hai vị trí mà tại đó vân sáng của hai bức xạ trùng nhau ⟹ ứng với vị trí vân sáng bậc k1 = 4 và k1 = 8 (suy luận, k < 10).
* Vị trí vân sáng trùng đầu tiên: k1l1 = k2l2 ⟹ 4´420 = k2l2 2,47 ≤ k2 ≤ 4,09.
* Do k1 = 4 (chẵn) ⟹ k2 = 3 (lẻ) ⟹ l2 = 0,56 mm = 560 nm.
⟹ Dl = l2 - l1 = 560 - 420 = 140 nm.