Thi Online (2023) Đề thi thử Vật Lí Sở Hà Tĩnh Lần 1 có đáp án
Thi Online (2023) Đề thi thử Vật Lí Sở Hà Tĩnh Lần 1 có đáp án
-
1026 lượt thi
-
40 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cường độ dòng điện được đo bằng dụng cụ nào sau đây?
 Xem đáp án
Xem đáp án
Công tơ điện- đo điện năng tiêu thụ.
Phong vũ biểu- đo áp suất khí quyển
Ampe kế - đo cường độ dòng điện.
Vôn kế- đo hiệu điện thế.
Đáp án C
Câu 2:
Một thấu kính có tiêu cự \(f(\;{\rm{m}})\). Độ tụ của thấu kính được xác định bởi
 Xem đáp án
Xem đáp án
Độ tụ của thấu kính tỉ lệ nghịch với tiêu cự f(m).
Đáp án B
Câu 3:
Một con lắc lò xo đang dao động điều hòa, đại lượng nào sau đây ti lệ với độ lớn lực kéo về?
 Xem đáp án
Xem đáp án
Gia tốc tỉ lệ với lực kéo về: F=ma.
Đáp án A
Câu 4:
Phát biểu nào dưới đây sai? Lực từ là lực tương tác
 Xem đáp án
Xem đáp án
Các điện tích đứng yên không sinh ra từ trường.
Đáp án D
Câu 5:
Một khung dây tạo ra suất điện động \({e_{\rm{c}}}\) trong thời gian \(\Delta t\). Đại lượng \({e_{\rm{c}}}\Delta t\) có đơn vị là
 Xem đáp án
Xem đáp án
Niutơn trên mét \(({\rm{N}}/{\rm{m}})\)- đơn vị của độ cứng lò xo.
Vôn trên mét ( \({\rm{V}}/{\rm{m}})\)- đơn vị cường độ điện trường.
Vêbe \(({\rm{Wb}})\).- đơn vị từ thông . Suất điện động được xác định bằng tốc độ biến thiên của từ thông theo thời gian \(e = - \frac{{\Delta \phi }}{{\Delta t}}\) nên \({e_{\rm{c}}}\Delta t\) có đơn vị của từ thông.
Tesla (T)- đơn vị cảm ứng từ B.
Đáp án C
Câu 6:
Một vật dao động điều hòa với phương trình \(x = 4\cos \left( {5\pi t + \frac{\pi }{3}} \right){\rm{cm}}\). Pha ban đầu của dao động là
 Xem đáp án
Xem đáp án
\(6{\rm{rad}}\) - chỉ có thế là lỗi đánh máy.
\(\left( {5\pi t + \frac{\pi }{3}} \right)\)rad- pha của dao động tại thời điểm t bất kì.
\(5\pi \) rad- tần số góc của dao động.
\(\frac{\pi }{3}{\rm{rad}}\)- pha ban đầu.
Đáp án D.
Câu 7:
Một xe buýt đang đứng yên nhưng không tắt máy, hành khách ngồi trên xe nhận thấy thân xe dao động. Dao động đó là
 Xem đáp án
Xem đáp án
dao động cưỡng bức- tần số dao động của xe phụ thuộc vào tần số dao động của động cơ.
dao động duy trì- không đúng vì không có yếu tố bù năng lượng sau mỗi chù kỳ dao động.
dao động tự do- không đúng vì tần số dao động phụ thuộc vào điều kiện bên ngoài (tần số động cơ)
dao động tắt dần- không có sự giảm của biên độ.
Đáp án A.
Câu 8:
Một điện tích \(q\) đặt trong điện trường đều có vectơ cường độ điện trường \(\vec E\) thì lực điện tác dụng lên điện tích được xác định bởi
 Xem đáp án
Xem đáp án
\(\vec F = q\vec E\) - biểu thức đúng.
Đáp án C
Câu 9:
Một con lắc đơn có chiều dài \(\ell \) đang dao động điều hòa, tại nơi có gia tốc trọng trường \(g\). Tần số dao động của con lắc được xác định bởi
 Xem đáp án
Xem đáp án
\(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{\ell }} \) - biểu thức đúng.
Các biểu thức còn lại đều sai về mặt thứ nguyên.
Đáp án B
Câu 10:
Trong thí nghiệm xác định gia tốc trọng trường \(g\) bằng con lắc đơn, kết quả của phép đo được ghi dưới dạng \(g = \bar g \pm \Delta g\). Sai số tỉ đối của phép đo được xác định bởi
 Xem đáp án
Xem đáp án
\(\delta g = \frac{{\Delta g}}{{\bar g}}\) - biểu thức đúng.
Các biểu thức còn lại đều sai về mặt thứ nguyên.
Đáp án A
Câu 11:
Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình là \({x_1} = {A_1}\cos \omega t\) và \({x_2} = {A_2}\cos \left( {\omega t + \frac{\pi }{2}} \right)\). Biên độ dao động tổng hợp của vật là
 Xem đáp án
Xem đáp án
\({A_1} + {A_2}\)- phù hợp cho hai dao động cùng pha.
\(\sqrt {A_1^2 + A_2^2} \)- phù hợp cho hai dao động vuông pha.
\(\sqrt {\left| {A_1^2 - A_2^2} \right|} \)- biểu thức này ko chính xác.
\(\left| {{A_1} - {A_2}} \right|\)- phù hợp cho trường hợp ngược pha.
Đáp án B.
Câu 12:
Một con lắc lò xo có tần số dao động riêng \({f_0}\). Khi tác dụng vào nó một ngoại lực cưỡng bức tuần hoàn có tần số \(f\) thì xảy ra hiện tượng cộng hưởng. Hệ thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
\(f = {f_0}\)- hiện tượng cộng hưởng xảy ra khi tần số ngoại lực bằng tần số riêng của hệ.
Đáp án A.
Câu 13:
 Xem đáp án
Xem đáp án
\(k = \frac{{F{r^2}}}{{\left| {{q_1}{q_2}} \right|}} \Rightarrow \frac{{N{m^2}}}{{C.C}}\)- Đáp án B.
Câu 14:
Một con lắc đơn có khối lượng \(m\), chiều dài \(\ell \) đang dao động điều hòa, tại nơi có gia tốc trọng trường \(g\). Lực kéo về \({P_{\rm{t}}}\) liên hệ với li độ cong \(s\) theo biểu thức \({P_{\rm{t}}} = - ks\). Hệ số \(k\) bằng
 Xem đáp án
Xem đáp án
\({P_t} = - mg\sin \alpha = - mg\frac{s}{l} = - \frac{{mg}}{l}s\)- Đáp án D.
Câu 15:
Cho một vật dao động điều hòa theo phương trình \(x = A\cos (\omega t + \varphi ),A > 0\). Trong phương trình đó, \(A\) gọi là
 Xem đáp án
Xem đáp án
biên độ dao động là A.
pha ban đầu của dao động \(\varphi \)
li độ dao động x.
\(\cos (\omega t + \varphi )\) pha của dao động tại thời điểm \(t\).
Đáp án A.
Câu 16:
Cho hai dao động điều hòa cùng phương, cùng tần số. Biên độ dao động tổng hợp của hai dao động này có giá trị nhỏ nhất khi độ lệch pha của hai dao động bằng
 Xem đáp án
Xem đáp án
Câu 17:
Bản chất dòng điện trong chất điện phân là
 Xem đáp án
Xem đáp án
Trong chất điện phân có ion dương và ion âm. Ion dường chuyển động cùng chiều với chiều điện trường, ion âm thì ngược lại. Đáp án C.
Câu 18:
Độ lớn suất điện động tự cảm của mạch điện tỉ lệ thuận với
 Xem đáp án
Xem đáp án
Tự cảm là trường hợp đặc biệt của hiện tượng cảm ứng điện từ: \({e_{tc}} = - L\frac{{\Delta i}}{{\Delta t}}\). Đáp án B.
Câu 19:
Khi nói về dao động tắt dần của một vật, phát biểu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Trong dao dộng tắt dần, biên độ và năng lượng giảm dần theo thời gian. Nếu đó do động tắt dần chậm thì chu kỳ dao động không thay đổi.
Gia tốc, vận tốc, li độ của vật dao động tắt dần biến đổi theo hàm cos theo thời gian. (biên độ của hàm cos giảm dần).
Đáp án D.
Câu 20:
Một trong những kết quả thu được của bài thực hành khảo sát thực nghiệm các định luật dao động của con lắc đơn là bình phương của chu kì tỉ lệ thuận với chiều dài con lắc \({T^2} = a\ell \). Kết quả này giúp chúng ta xác định được gia tốc rơi tự do \(g\) qua công thức
 Xem đáp án
Xem đáp án
\[T = 2\pi \sqrt {\frac{\ell }{g}} \Rightarrow {T^2} = \frac{{4{\pi ^2}}}{g}\ell \]. Đáp án B.
Câu 21:
Trong bài thực hành đo gia tốc trọng trường bằng con lắc đơn, một nhóm học sinh đã vẽ đồ thị sự phụ thuộc của chu kì dao động \(T\) vào chiều dài \(\ell \) của con lắc. Đồ thị nào sau đây minh họa sự phụ thuộc trên?
 Xem đáp án
Xem đáp án
\[T = 2\pi \sqrt {\frac{\ell }{g}} \Rightarrow {T^2} = \frac{{4{\pi ^2}}}{g}\ell \]. Đáp án C.
Câu 22:
Một vật dao động điều hòa với biên độ \(6\;{\rm{cm}}\), chu kì \(0,5\;{\rm{s}}\). Tốc độ cực đại của vật là
 Xem đáp án
Xem đáp án
\[{v_{{\rm{max}}}} = \frac{{2\pi }}{T}.A = 24\pi (cm/s)\]. Đáp án C.
Câu 23:
Trong mỗi chu kì, biên độ dao động của một con lắc giảm đi \(4\% \) thì cơ năng của con lắc giảm đi
 Xem đáp án
Xem đáp án
\[\frac{{\Delta E}}{E} = \frac{{\frac{1}{2}K{A^2} - \frac{1}{2}K{{\left( {0,96A} \right)}^2}}}{{\frac{1}{2}K{A^2}}} \times 100 = 7,84\% \]. Đáp án D.
Câu 24:
Vật dao động điều hòa theo phương trình \(x = A\cos \omega t(\omega > 0)\). Ở thời điểm \(t = \frac{\pi }{{4\omega }}\), vật có li độ \(2\sqrt 2 \;{\rm{cm}}\). Biên độ dao động của vật là
 Xem đáp án
Xem đáp án
\(x = A\cos \omega t \Rightarrow 2\sqrt 2 = A.\cos \frac{\pi }{4} \Rightarrow A = 4cm\). Đáp án C.
Câu 25:
Một vật dao động với phương trình \(x = A\cos 2\pi t,t\) tính bằng \({\rm{s}}\). Dao động này được biểu diễn bằng một vectơ quay. Tốc độ quay của vectơ này là
 Xem đáp án
Xem đáp án
\(f = \frac{\omega }{{2\pi }} = \frac{{2\pi }}{{2\pi }} = 1\)(vòng/s). Đáp án B.
Câu 26:
Vật sáng AB đặt vuông góc với trục chính của một thấu kính phân kì, cách thấu kính \(60\;{\rm{cm}}\), cho ảnh ảo A’B’ cách thấu kính \(15\;{\rm{cm}}\). Tiêu cự thấu kính là
 Xem đáp án
Xem đáp án
\[\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Rightarrow f = \frac{{60 \times ( - 15)}}{{60 + ( - 15)}} = - 20cm\]. Đáp án D.
Câu 27:
Một vật dao động điều hòa với phương trình \(x = 6\cos \left( {\omega t - \frac{{2\pi }}{3}} \right){\rm{cm}}\), với \(\omega > 0\). Kể từ \(t = 0\) đến \(t = \frac{1}{6}\;{\rm{s}}\), vật đi được quãng đường \(9\;{\rm{cm}}\). Giá trị của \(\omega \) là
 Xem đáp án
Xem đáp án
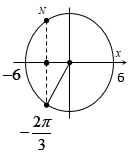
Từ đường tròn lượng giác ta suy ra: \(\omega = \frac{{\frac{{2\pi }}{3}}}{{\frac{1}{6}}} = 4\pi \)rad/s.
Đáp án C.
Câu 28:
Có 4 nguồn điện giống nhau, mỗi nguồn có suất điện động \(2\;{\rm{V}}\) và điện trở trong \(0,5\Omega \) được mắc nối tiếp. Suất điện động và điện trở trong của bộ nguồn là
 Xem đáp án
Xem đáp án
\({\xi _b} = 4.2 = 8V,{r_b} = 0,5.4 = 2\Omega \). Đáp án D.
Câu 29:
Ánh sáng truyền từ môi trường (1) có chiết suất \({n_1} = \frac{4}{3}\) sang môi trường (2) có chiết suất \({n_2} = 1,5\). Chiết suất tỉ đối của môi trường (1) đối với môi trường (2) bằng
 Xem đáp án
Xem đáp án
Chiết suất tỉ đối \({n_{12}} = \frac{{{n_1}}}{{{n_2}}} = \frac{{\frac{4}{3}}}{{1,5}} = \frac{8}{9}\). Đáp án C.
Câu 30:
Một dây dẫn uốn thành vòng tròn mang dòng điện có cường độ \(10\;{\rm{A}}\) đặt trong không khí, cảm ứng từ tại tâm của nó có độ lớn \(\pi \cdot {10^{ - 5}}\;{\rm{T}}\). Bán kính của vòng dây đó là
 Xem đáp án
Xem đáp án
\(B = 2\pi {.10^{ - 7}}\frac{I}{R} \Rightarrow R = 20cm\). Đáp án D.
Câu 31:
Một con lắc lò xo gồm vật nặng gắn vào lò xo có độ cứng \(50\;{\rm{N}}/{\rm{m}}\) dao động điều hòa trên đoạn MN có chiều dài \(8\;{\rm{cm}}\). Động năng của vật khi nó cách M một khoảng \(3\;{\rm{cm}}\) là
 Xem đáp án
Xem đáp án
\(\left\{ \begin{array}{l}A = 4cm.\\x = 4 - 3 = 1cm\\{E_{\rm{d}}} = \frac{1}{2}K\left( {{A^2} - {x^2}} \right) = \frac{1}{2}50.(0,{04^2} - 0,{01^2}) = 0.0375J\\\end{array} \right.\) Đáp án A.
Câu 32:
Một con lắc lò xo có độ cứng \(k = 100\;{\rm{N}}/{\rm{m}}\) dao động điều hòa dưới tác dụng của lực kéo về có phương trình \(F = 5\cos (2\pi t + 5\pi /6){\rm{N}},t\) tính bằng s. Cho \({\pi ^2} = 10\). Biểu thức vận tốc của vật là
 Xem đáp án
Xem đáp án
\(A = \frac{{{F_0}}}{K} = \frac{5}{{100}} = 5cm \to {v_{{\rm{max}}}} = 2\pi .5 = 10\pi cm/s\).
F cùng pha với gia tốc a; gia tốc a sớm pha π/2 so với vận tốc v.
\({\varphi _v} = {\varphi _F} - \frac{\pi }{2} = \frac{{5\pi }}{6} - \frac{\pi }{2} = \frac{\pi }{3}\)
Đáp án B.
Câu 33:
Con lắc lò xo treo thẳng đứng dao động điều hòa với biên độ \(8\;{\rm{cm}}\). Cho \(g = {\pi ^2}\) \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\). Biết trong một chu ki dao động thời gian lò xo bị dãn gấp đôi thời gian lò xo bị nén. Thời gian lò xo bị dãn trong một chu kì là
 Xem đáp án
Xem đáp án

\(\left\{ \begin{array}{l}{t_d} = 2{t_n} \Rightarrow \Delta {\varphi _{nen}} = \frac{{2\pi }}{3} \Rightarrow \Delta {l_0} = \frac{A}{2} = 4cm.\\T = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} = 0,4s\\{t_d} = \frac{2}{3}T\end{array} \right. \Rightarrow {t_d} = \frac{4}{{15}}s\). Đáp án: A
Câu 34:
Tại một nơi trên mặt đất, người ta thực hiện đo chu kì dao động điều hòa của con lắc đơn. Khi chiều dài con lắc là \({\ell _1}\) thì chu kì là \(1,5\;{\rm{s}}\), khi chiều dài con lắc là \({\ell _2}\) thì chu kì là \(2,4\;{\rm{s}}\). Chu kì của con lắc có chiều dài \(2{\ell _1} + 3{\ell _2}\) là
 Xem đáp án
Xem đáp án
\(\left\{ \begin{array}{l}T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow {T^2} \sim l\\l = 2{l_1} + 3{l_2}\end{array} \right. \Rightarrow {T^2} = 2T_1^2 + 3T_2^2 \Rightarrow T = 4,7s\). Đáp án: B.
Câu 35:
Một con lắc đơn có chiều dài dây treo bằng \(60\;{\rm{cm}}\) đang dao động điều hòa. Khi dây treo hợp với phương thẳng đứng một góc \({8^^\circ }\) thì tốc độ của vật là \(20\;{\rm{cm}}/{\rm{s}}\). Lấy \(g = 9,8\;{\rm{m}}/{{\rm{s}}^2}\). Góc lệch nhỏ nhất giữa dây treo so với phương nằm ngang bằng
 Xem đáp án
Xem đáp án
\[\left\{ \begin{array}{l}S_0^2 = {s^2} + \frac{{{v^2}}}{{{\omega ^2}}}\\\omega = \sqrt {\frac{g}{l}} \\{S_0} = {\alpha _0}l\\s = \alpha .l\end{array} \right. \Rightarrow {\alpha _0} = \sqrt {{\alpha ^2} + \frac{{{v^2}}}{{g.l}}} = 9,{3^0}\]. Suy ra góc lệch nhỏ nhất của dây treo và phương ngang \(\beta = {90^0} - 9,{3^0} = 80,{7^0}\). Đáp án A.
Câu 36:
Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình \({x_1} = 6\cos \left( {10t - \frac{\pi }{2}} \right){\rm{cm}}\) và \({x_2} = 12\cos \left( {10t + \frac{\pi }{6}} \right){\rm{cm}}\) ( \(t\) tính bằng \(\left. {\rm{s}} \right)\). Cho khối lượng của vật là \(100\;{\rm{g}}\). Động năng của vật tại thời điểm \(t = 0,15\;{\rm{s}}\) là
 Xem đáp án
Xem đáp án
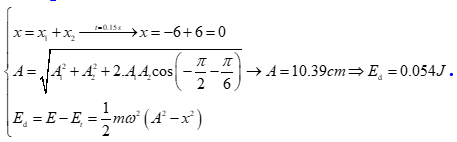
Câu 37:
Một lò xo nhẹ có một đầu gắn với vật nặng có khối lượng \(m\), đầu còn lại được treo lên trần một xe ôtô. Ôtô chạy đều trên đường thẳng, cứ qua một khoảng như nhau bánh xe lại gặp một cái mô nhỏ, làm cho con lắc bị kích thích dao động. Con lắc dao động mạnh nhất khi xe có tốc độ \(v\). Nếu treo thêm vật nặng có khối lượng \(3\;{\rm{m}}\) vào đầu dưới lò xo thì con lắc dao động mạnh nhất khi tốc độ của xe là
 Xem đáp án
Xem đáp án
- Đây là trường hợp cộng hưởng trong dao động cưỡng bức
- Điều kiện cộng hưởng được viết: \(\left\{ \begin{array}{l}{T_1} = {T_0} \Rightarrow \frac{S}{{{v_1}}} = 2\pi \sqrt {\frac{m}{k}} \\{T_2} = {T_0} \Rightarrow \frac{S}{{{v_2}}} = 2\pi \sqrt {\frac{{4m}}{k}} \end{array} \right. \Rightarrow {v_2} = \frac{{{v_1}}}{2}\). Đáp án:D.
Câu 38:
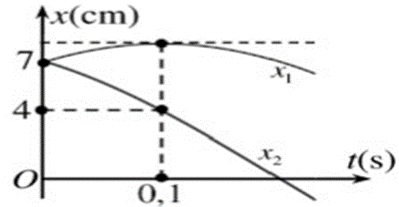
Dao động của một chất điểm là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ, có li độ \({x_1}\) và \({x_2}\) phụ thuộc thời gian như hình vẽ. Tốc độ cực đại của chất điểm gần giá trị nào nhất sau đây?
 Xem đáp án
Xem đáp án
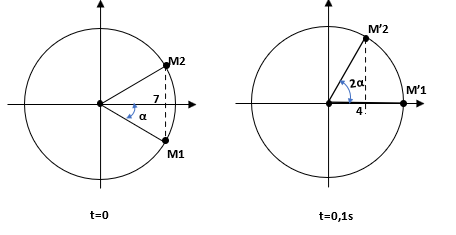
\[\left\{ \begin{array}{l}\cos \alpha = \frac{7}{A}\\\cos 2\alpha = \frac{4}{A}\end{array} \right. \Rightarrow \cos 2\alpha = 2.{\cos ^2}\alpha - 1 \Rightarrow A = 8,099cm\]
Suy ra:
\[\begin{array}{l}\left\{ {\cos {\varphi _1} = \cos {\varphi _2} = \frac{7}{{8,099}}} \right. \Rightarrow \left\{ \begin{array}{l}{\varphi _1} = - 0.527rad\\{\varphi _2} = 0.527rad\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2.{A_1}.{A_2}{\rm{cos}}\left( {{\varphi _2} - {\varphi _1}} \right)} = 14cm.\\\omega = \frac{{0.527}}{{0,1}} = 5,27s.\end{array} \right.\\ \Rightarrow {v_{{\rm{max}}}} = \omega A = 73.78cm/s\end{array}\]
Đáp án: A.
Câu 39:
Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang. Công suất \(P\) được xác định bởi tích của lực kéo về và vận tốc của vật là đại lượng đặc trưng cho tốc độ chuyển hóa giữa thế năng và động năng. Hình bên là đồ thị biểu diễn sự phụ thuộc của \(P\) theo thời gian \(t\). Tại thời điểm ban đầu \(t = 0\), vật cách vị trí cân bằng \(5\;{\rm{cm}}\). Độ cứng của lò xo là
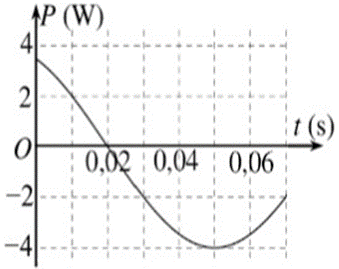
 Xem đáp án
Xem đáp án
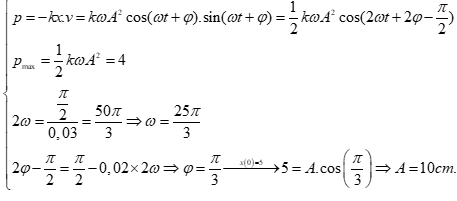
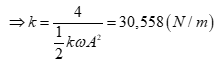
Câu 40:
Trên một mặt bảng thẳng đứng có hai chiếc đinh cố định vuông góc với mặt bảng tại hai điểm M và N, hai điểm này cùng nằm trên một đường thẳng đứng và cách nhau một khoảng \(20\;{\rm{cm}}\). Một con lắc đơn có chiều dài dây 80 cm được treo vào đinh tại M như hình vẽ. Kéo con lắc ra theo phương song song với mặt bảng cho dây treo lệch với phương thẳng đứng một góc \({6^^\circ }\), rồi thả nhẹ cho vật dao động tự do. Lấy \(g = 9,8\;{\rm{m}}/{{\rm{s}}^2}\). Tốc độ trung bình của vật trong một dao động toàn phần là
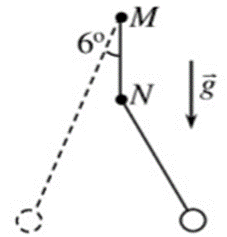
 Xem đáp án
Xem đáp án
\[\left\{ \begin{array}{l}\frac{1}{2}mg{l_1}\left( {1 - \cos {\alpha _{01}}} \right) = \frac{1}{2}mg{l_2}\left( {1 - \cos {\alpha _{02}}} \right) \Rightarrow {\alpha _{02}} = 6,{93^0}\\{T_1} = 2\pi \sqrt {\frac{{{l_1}}}{g}} = 1,79s\\{T_2} = 2\pi \sqrt {\frac{{{l_2}}}{g}} = 1,55s\end{array} \right.\]
\[\left\{ \begin{array}{l}{v_{tb}} = \frac{{{S_{01}} + {S_{02}}}}{{\frac{{{T_1}}}{4} + \frac{{{T_2}}}{4}}}\\{v_{tb}} = \frac{{80.\sin {6^0} + 60.\sin 6,{{93}^0}}}{{\frac{{1,79}}{4} + \frac{{1,55}}{4}}} = 18,68cm/s\end{array} \right.\].
Đáp án:A.
