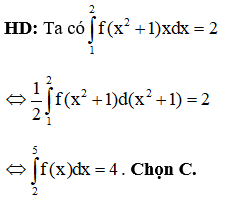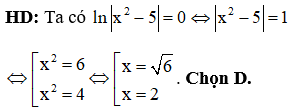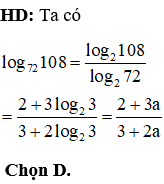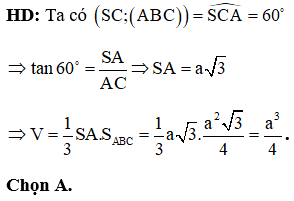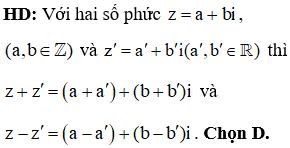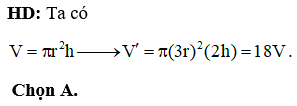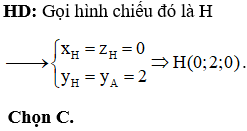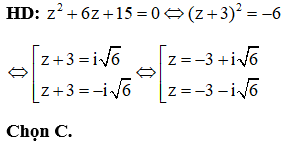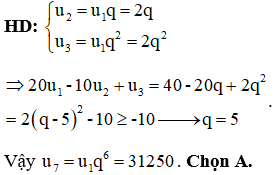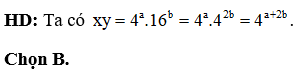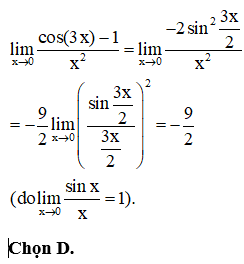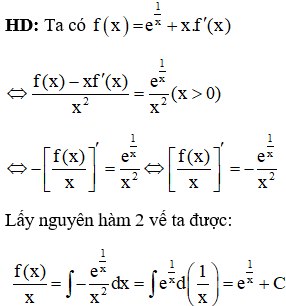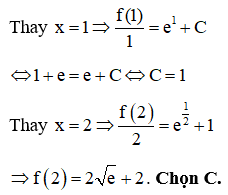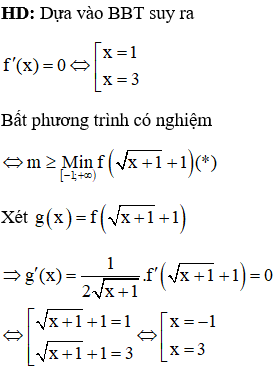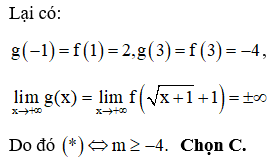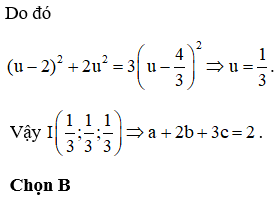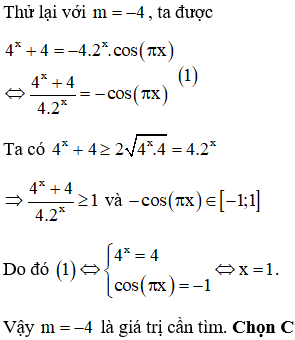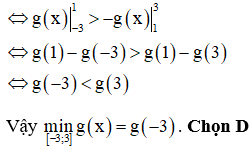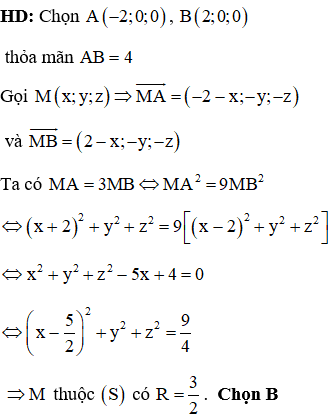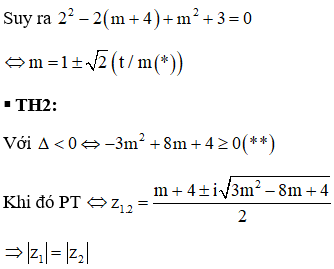50 câu hỏi trắc nghiệm thuộc 30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 28)

Câu 1:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y - 6 z + 5 = 0$ . Mặt phẳng tiếp xúc với (S) và song song với mặt phẳng $(P) : 2 x - y + 2 x - 11 = 0$ có phương trình là

A. $2 x - y - 2 z + 7 = 0$

B. $2 x - y + 2 z - 7 = 0$

C. $2 x - y + 2 z + 9 = 0$

D. $2 x - y + 2 z - 9 = 0$

Xem đáp án

Câu 2:

Cho $\int_{1}^{2} f (x^{2} + 1) x d x = 2$ . Khi đó $I = \int_{2}^{5} f (x) d x$ bằng

A. 1

B. 2

C. 4

D. -1

Xem đáp án

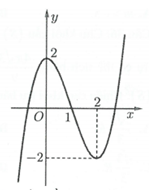
Câu 3:

Cho hàm số y = f(x) có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng

A. 0

B. 3

C. 2

D. 1

Xem đáp án

HD: Đồ thị hàm số có tiệm cận đứng là x = -2 và x = 0, tiệm cận ngang là y = 0. Chọn B.

Câu 4:

Số nghiệm dương của phương trình $\ln |x^{2} - 5| = 0$ là

A. 1

B. 4

C. 0

D. 2

Xem đáp án

Câu 5:

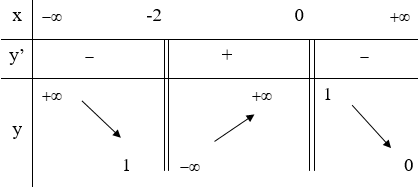
Cho hàm số y = f(x) có bảng xét dấu như sau

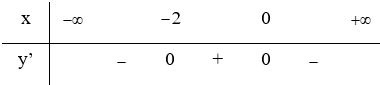
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?

A. (-2;0)

B. (-3;1)

C. $(0; + \infty)$

D. $(- \infty; - 2)$

Xem đáp án

HD: Hàm số đã cho đồng biến trên (-2;0). Chọn A.

Câu 6:

Trong không gian Oxyz, cho mặt phẳng $(P) : 2 x - 2 y + z - 1 = 0$ . Khoảng cách từ điểm M(1;-2;0) đến mặt phẳng (P) bằng

A. 2

B. $\frac{5}{3}$

C. $\frac{4}{3}$

D. 5

Xem đáp án

Câu 7:

Nếu $\log_{2} 3 = a$ thì $\log_{72} 108$ bằng

A. $\frac{3 + 2 a}{2 + 3 a}$

B. $\frac{2 + 3 a}{2 + 2 a}$

C. $\frac{2 + a}{3 + a}$

D. $\frac{2 + 3 a}{3 + 2 a}$

Xem đáp án

Câu 8:

Số hạng không chứa x trong khai triển ${(\frac{x}{2} + \frac{4}{x})}^{20} (x \neq 0)$ bằng

A. $2^{9} C_{20}^{9}$

B. $2^{10} C_{20}^{10}$

C. $2^{10} C_{20}^{11}$

D. $2^{8} C_{20}^{12}$

Xem đáp án

Câu 9:

Một vật chuyển động với vận tốc $v (t) = 3 t^{2} + 4 (m / s)$ , trong đó t là khoảng thời gian tính bằng giây. Tính quãng đường vật đó đi được trong khoảng thời gian từ giây thứ 3 đến giây thứ 10?

A. 945m

B. 994m

C. 471m

D. 1001m

Xem đáp án

Câu 10:

Nếu các số hữu tỉ a,b thỏa mãn $\int_{0}^{1} (a e^{x} + b) d x = e + 2$ thì giá trị của biểu thức a+b bằng

A. 4

B. 5

C. 6

D. 3

Xem đáp án

Câu 11:

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết đường thẳng SC hợp với mặt phẳng đáy một góc $60 °$ . Thể tích của khối chóp S.ABC bằng

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3}}{2}$

C. $\frac{a^{3}}{8}$

D. $\frac{3 a^{3}}{4}$

Xem đáp án

Câu 12:

Biết đường thẳng y = x - 2 cắt đồ thị hàm số $y = \frac{2 x + 1}{x - 1}$ tại hai điểm phân biệt A, B có hoành độ lần lượt $x_{A}, x_{B}$ . Khi đó giá trị của $x_{A} + x_{B}$ bằng

A. 3

B. 5

C.1

D. 2

Xem đáp án

Câu 13:

Cho tập hợp M gồm 15 điểm phân biêt. Số vecto khác $\vec{0}$ , có điểm đầu và điểm cuối là các điểm thuộc M là

A. $C_{15}^{2}$

B. $15^{2}$

C. $A_{15}^{2}$

D. $A_{15}^{13}$

Xem đáp án

Chọn C.

Câu 14:

Cho hai số phức $z_{1} = 4 - 2 i$ và $z_{2} = 1 + 5 i$ . Tìm số phức $z = z_{1} + z_{2}$

A. z = 3 - 7i

B. z = -2 + 6i

C. z = 5 - 7i

D. z = 5 + 3i

Xem đáp án

Câu 15:

Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên

Khẳng định nào dưới đây sai?

A. $x_{0} = 0$ là điểm cực đại của hàm số

B. M(0;2) là điểm cực tiểu của đồ thị hàm số

C. $x_{0} = 1$ là điểm cực tiểu của hàm số

D. f(-1) là một giá trị cực tiểu của hàm số

Xem đáp án

HD: Ta có A, C, D đúng còn B sai vì M(0;2) là điểm cực đại của đồ thị hàm số. Chọn B.

Câu 16:

Hỏi nếu tăng chiều cao của một khối trụ lên gấp 2 lần và tăng bán kính đáy của nó lên gấp 3 lần thì thể tích của khối trụ mới sẽ tăng bao nhiêu lần so với thể tích khối trụ ban đầu?

A. 18 lần

B. 36 lần

C. 12 lần

D. 6 lần

Xem đáp án

Câu 17:

Trong không gian Oxyz, cho điểm A(1;2;-1). Tọa độ hình chiếu vuông góc của điểm A trên trục Oy là

A. (1;0;-1)

B. (0;0;-1)

C. (0;2;0)

D. (1;0;0)

Xem đáp án

Câu 18:

Đồ thị hàm số y = ln x đi qua điểm

A. B(0;1)

B. $C (2; e^{2})$

C. D(2e;e)

D. A(1;0)

Xem đáp án

HD: Ta có ĐTHS y = ln x đi qua điểm có tọa độ (1;0) vì ln 1 = 0. Chọn D.

Câu 19:

Cho hàm số y = f(x) có bảng biến thiên trên [-5;7) như sau

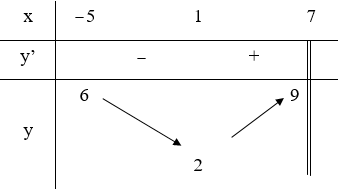
Mệnh đề nào dưới đây đúng?

A. $\underset{[- 5; 7)}{m i n} f (x) = 2$

B. $\underset{[- 5; 7)}{m a x} f (x) = 6$

C. $\underset{[- 5; 7)}{m i n} f (x) = 6$

D. $\underset{[- 5; 7)}{m a x} f (x) = 9$

Xem đáp án

HD: Trên [-5;7), hàm số có GTNN bằng 2, đạt được khi x = 1. Chọn A.

Câu 20:

Nghiệm của phương trình $z^{2} + 6 z + 15 = 0$ là

A. $3 \pm \sqrt{6} i$

B. $- 6 \pm 2 \sqrt{6} i$

C. $- 3 \pm \sqrt{6} i$

D. $6 \pm 2 \sqrt{6} i$

Xem đáp án

Câu 21:

Cho cấp số nhân $(u_{n})$ có $u_{1} = 2$ và biểu thức $20 u_{1} - 10 u_{2} + u_{3}$ đạt giá trị nhỏ nhất. Số hạng thứ bảy của cấp số nhân $(u_{n})$ có giá trị bằng

A. 31250

B. 6250

C. 136250

D. 39062

Xem đáp án

Câu 22:

Trong không gian Oxyz, cho điểm M(-3;9;6). Gọi $M_{1}, M_{2}, M_{3}$ lần lượt là hình chiếu vuông góc của M trên các trục tạo độ Ox, Oy, Oz. Mặt phẳng $(M_{1} M_{2} M_{3})$ có phương trình là

A. $\frac{x}{- 3} + \frac{y}{9} + \frac{z}{6} = 0$

B. $\frac{x}{3} + \frac{y}{- 9} + \frac{z}{- 6} = 0$

C. $\frac{x}{- 3} + \frac{y}{9} + \frac{z}{6} = 1$

D. $\frac{x}{- 1} + \frac{y}{3} + \frac{z}{2} = 1$

Xem đáp án

Câu 23:

Biết rằng $4^{a} = x v à 16^{b} = y$ . Khi đó xy bằng

A. $64^{a b}$

B. $4^{a + 2 b}$

C. $4^{2 a b}$

D. $16^{a + 2 b}$

Xem đáp án

Câu 24:

Đồ thị hàm số $y = \frac{6 x^{2} - 5 x + 1}{2 x^{2} + 9 x - 5}$ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

A. 2

B. 3

C. 4

D. 1

Xem đáp án

Vậy đồ thị hàm số có tất cả 2 đường tiệm cận, trong đó có một tiệm cận đứng và một tiệm cận ngang. Chọn A.

Câu 25:

$\underset{x \to 0}{l i m} \frac{\cos (3 x) - 1}{x^{2}}$ bằng

A. $\frac{9}{2}$

B. $- \frac{3}{2}$

C. $- \frac{2}{3}$

D. $- \frac{9}{2}$

Xem đáp án

HD: Cách 1: (Sử dụng giới hạn cơ bản)

Cách 2: ( Sử dụng quy tắc Lopital)

Câu 26:

Trong không gian Oxyz, cho hai mặt phẳng $(P) : 2 x - y + 2 z - 4 = 0$ và $(Q) : 2 x - y + 2 z + 5 = 0$ . Mặt cầu (S) tiếp xúc với hai mặt phẳng (P) và (Q) có bán kính bằng

A. 3

B. $\frac{3}{2}$

C. 9

D. $\frac{1}{2}$

Xem đáp án

Câu 27:

Cho $\int_{0}^{4} f (x) d x = 2018$ . Giá trị $\int_{0}^{2} f (2 x) d x + \int_{- 2}^{2} f (2 - x) d x$ bằng

A. 4036

B. 3027

C. 0

D. -1009

Xem đáp án

Câu 28:

Cho hàm số $f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ)$ . Đồ thị của hàm số y = f(x) như hình vẽ bên. Có bao nhiêu số nguyên m thuộc khoảng (-20;20) để phương trình $(2 m - 1) f (x) - 3 = 0$ có đúng ba nghiệm phân biệt?

A. 39

B. 38

C. 37

D. 36

Xem đáp án

Câu 29:

Cho hàm số f(x) xác định và có đạo hàm trên khoảng $(0; + \infty)$ , đồng thời thỏa mãn điều kiện $f (1) = 1 + e, f (x) = e^{\frac{1}{x}} + x . f' (x), \forall x \in (0; + \infty)$ . Giá trị của f(2) bằng

A. $1 + 2 \sqrt{e}$

B. $1 + \sqrt{e}$

C. $2 + 2 \sqrt{e}$

D. $2 + \sqrt{e}$

Xem đáp án

Câu 30:

Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-2). Gọi (P) là mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC. Viết phương trình mặt cầu tâm O và tiếp xúc với mặt phẳng (P)?

A. $x^{2} + y^{2} + z^{2} = 81$

B. $x^{2} + y^{2} + z^{2} = 3$

C. $x^{2} + y^{2} + z^{2} = 9$

D. $x^{2} + y^{2} + z^{2} = 25$

Xem đáp án

Câu 31:

Cường độ ánh sáng đi qua môi trường nước biển giảm dần theo công thức $I = I_{0} . e^{- μ x}$ , với $I_{0}$ là cường độ ánh sáng lúc ánh sáng bắt đầu đi vào môi trường nước biển và x là độ dày của môi trường đó (tính bằng đơn vị mét). Biết rằng môi trường nước biển có hằng số hấp thu $μ = 1, 4$ . Hỏi ở độ sâu 30 mét thì cường độ ánh sáng giảm đi bao nhiêu lần so với cường độ ánh sáng lúc ánh sáng bắt đầu đi vào nước biển?

A. $e^{21}$ lần

B. $e^{42}$ lần

C. $e^{- 21}$ lần

D. $e^{- 42}$ lần

Xem đáp án

Câu 32:

Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là

A. $\frac{5}{4} {πR}^{2}$

B. ${πR}^{2}$

C. $\frac{7}{4} {πR}^{2}$

D. $\frac{3}{2} {πR}^{2}$

Xem đáp án

HD: Gọi x, y lần lượt là khoảng cách từ tâm mặt cầu đến các đường tròn thiết diện

Tổng diện tích của hai hình tròn này là:

Câu 33:

Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3) và điểm M(a;b;0) sao cho tổng $M A^{2} + M B^{2}$ nhỏ nhất. Giá trị của a + b bằng

A. -2

B. 2

C. 3

D. 1

Xem đáp án

Câu 34:

Tập hợp tất cả các giá trị thực của tham số m để hàm số $y = \ln (x^{2} + 1) - m x + 1$ đồng biến trên R là

A. [-1;1]

B. $(- \infty; - 1)$

C. $(- \infty; - 1]$

D. (-1;1)

Xem đáp án

Câu 35:

Cho hàm số y = f(x) có bảng biến thiên

Tìm tất cả các giá trị của m để bất phương trình $f (\sqrt{x + 1} + 1) \leq m$ có nghiệm

A. m > -5

B. $m \geq 2$

C. $m \geq - 4$

D. $m \geq 1$

Xem đáp án

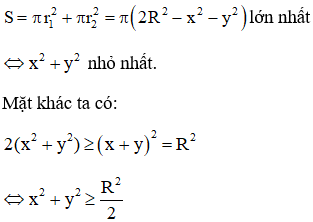
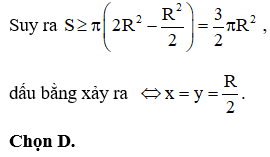
Câu 36:

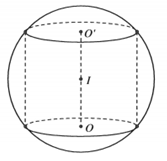
Cho khối cầu (S) có bán kính R. Một khối trụ có thể tích bằng $\frac{4 π \sqrt{3}}{9} R^{3}$ và nội tiếp khối cầu (S). Chiều cao khối trụ bằng

A. $\frac{2 \sqrt{3}}{3} R$

B. $\frac{\sqrt{2}}{2} R$

C. $\frac{\sqrt{3}}{3} R$

D. $R \sqrt{2}$

Xem đáp án

HD: Gọi h và r lần lượt là chiều cao và bán kính đáy của khối trụ

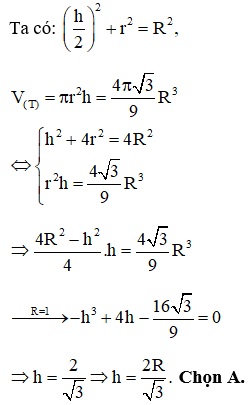
Câu 37:

Cho $M = C_{2019}^{0} + C_{2019}^{1} + C_{2019}^{2} + . . . + C_{2019}^{2019}$ . Viết M dưới dạng một số trong hệ thập phân thì số này có bao nhiêu chữ số?

A. 610

B. 608

C. 607

D. 609

Xem đáp án

HD: Xét khai triển:

Số chữ số của số đã cho bằng phân nguyên của số:

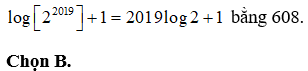
Câu 38:

Trong không gian Oxyz, cho hai mặt phẳng $(P) : 2 x - 2 y + z - 2 = 0$ và $(Q) : 2 x - y + z + 1 = 0$ . Số mặt cầu đi qua A(1;-2;1) và tiếp xúc với hai mặt phẳng (P), (Q) là

A. 1

B. 2

C. 0

D. Vô số

Xem đáp án

HD: Dễ thấy (P)//(Q). Gọi (R) là mặt phẳng song song và cách đều 2 mặt phằng (P) và (Q)

Câu 39:

Cho hai số thực dương x, y thỏa mãn $\log_{3} x = \log_{6} y = \log_{2} (x + y)$ . Biểu thức $P = \frac{1}{x^{2}} + \frac{1}{y^{2}}$ có giá trị bằng

A. 27

B. 36

C. 18

D. 45

Xem đáp án

Câu 40:

Trong không gian Oxyz, cho ba điểm $A (2; 0; 0), B (0; 2; 0), C (0; 0; 2)$ và D là điểm đối xứng của gốc tọa độ O qua mặt phẳng (ABC). Điểm I(a,b,c) là tâm mặt cầu đi qua bốn điểm A; B; C; D. Tính giá trị của biểu thức $P = a + 2 b + 3 c$

A. P = 0

B. P = 2

C. P = -2

D. P = 1

Xem đáp án

Câu 41:

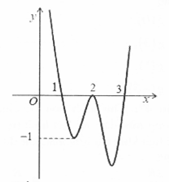
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số $y = f [f (x) + 2]$ có bao nhiêu điểm cực trị?

A. 12

B. 11

C. 9

D. 10

Xem đáp án

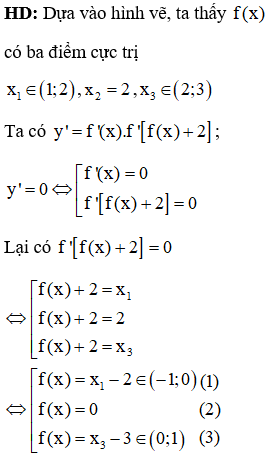
Dựa vào hình vẽ, ta thấy (1) có 3 nghiệm phân biệt; (2) có 2 nghiệm phân biệt; (3) có 3 nghiệm phân biệt và các nghiệm trên đều là nghiệm đơn hoặc bội lẻ

Vậy hàm số đã cho có 3 + 3 + 2 + 3 = 11 điểm cực trị. Chọn B

Câu 42:

Cho hàm số $y = x^{3} - 3 x$ có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng $y = k (x + 1) + 2$ cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M(-1;2), tính tích tất cả các phần tử của tập S.

A. $\frac{1}{9}$

B. $- \frac{2}{9}$

C. $\frac{1}{3}$

D. -1

Xem đáp án

HD: Hoành độ giao điểm của (C) và d là nghiệm phương trình:

Chọn

Câu 43:

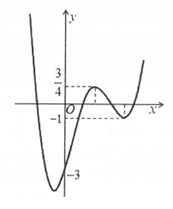
Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình $f (|x + m|) = m$ có 4 nghiệm phân biệt là

A. 0

B. Vô số

C. 2

D. 1

Xem đáp án

Phần 2: Lấy đối xứng phần 1 qua trục Oy

Câu 44:

Cho phương trình $2^{x} = \sqrt{m . 2^{x} \cos (πx - 4)}$ , với m là tham số thực. Gọi $m_{0}$ là giá trị của m sao cho phương trình trên có đúng một nghiệm thực. Khẳng định nào dưới đây đúng?

A. $m_{0}$ < -5

B. $m_{0}$ > 0

C. $m_{0} \in [- 5; 1)$

D. $m_{0} \in [- 1; 0)$

Xem đáp án

Câu 45:

Trong không gian Oxyz, cho tam giác ABC có các đỉnh B và C trên các cạnh AC, AB. Tọa độ hình chiếu A trên BC là

A. (2;0;0)

B. $(\frac{5}{3}; 0; 0)$

C. $(\frac{7}{2}; 0; 0)$

D. $(\frac{8}{3}; 0; 0)$

Xem đáp án

Câu 46:

Cho hàm số y = f(x) liên tục trên R có đồ thị $y = f' (x)$ như hình vẽ. Đặt $g (x) = 2 f (x) - {(x - 1)}^{2}$ . Khi đó giá trị nhỏ nhất của hàm số $y = g (x)$ trên đoạn [-3;3] bằng

A. g(0)

B. g(3)

C. g(1)

D. g(-3)

Xem đáp án

Câu 47:

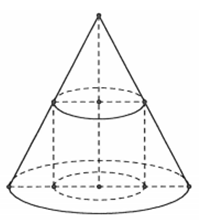
Cho hình nón có chiều cao 2R và bán kính đường tròn đáy R. Xét hình trụ nội tiếp hình nón sao cho thể tích khối trụ lớn nhất, khi đó bán kính đáy của khối trụ bằng

A. $\frac{2 R}{3}$

B. $\frac{R}{3}$

C. $\frac{R}{2}$

D. $\frac{3 R}{4}$

Xem đáp án

HD: Gọi r, h lần lượt là bán kính đáy, chiều cao của hình trụ

Hình trụ nội tiếp hình nón (tam giác đồng dạng)

Câu 48:

Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, CH vuông góc tại H, I là trung điểm của HC. Biết SI vuông góc với mặt phẳng đáy, Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, CH vuông góc tại H, I là trung điểm của HC. Biết SI vuông góc với mặt phẳng đáy, . Gọi O là trung điểm của đoạn AB, O' là tâm mặt cầu ngoài tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO' và mặt phẳng (ABC) là. Gọi O là trung điểm của đoạn AB, O' là tâm mặt cầu ngoài tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO' và mặt phẳng (ABC) là

A. $45 °$ $\hat{A S B} = 90 °$

B. $90 °$

C. $30 °$

D. $60 °$

Xem đáp án

Câu 49:

Trong không gian, cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm sao cho $M A = 3 M B$ là một mặt cầu. Bán kính của mặt cầu bằng

A. 3

B. $\frac{3}{2}$

C. $\frac{9}{2}$

D. 1

Xem đáp án

Câu 50:

Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình $z^{2} - (m + 4) z + m^{2} + 3 = 0$ có nghiệm phức $z_{0}$ thỏa mãn $|z_{0}| = 2$ . Số phần tử của tập hợp S là

A. 4

B. 3

C. 2

D. 1

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết

30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 28)

Danh sách câu hỏi

Bài thi liên quan