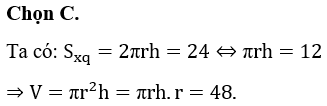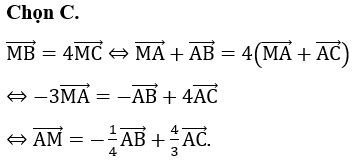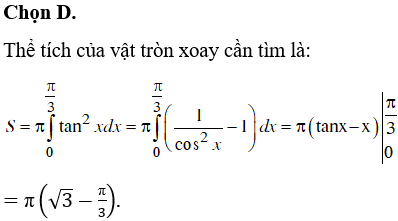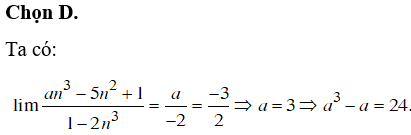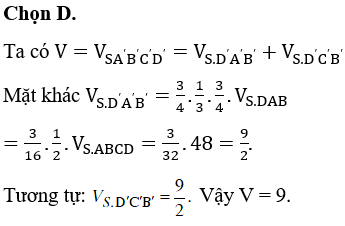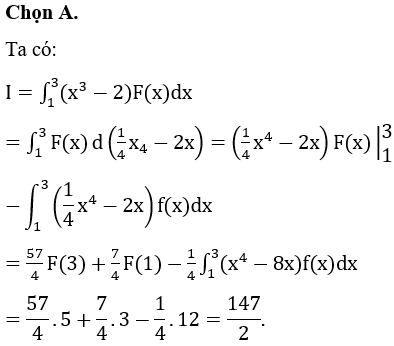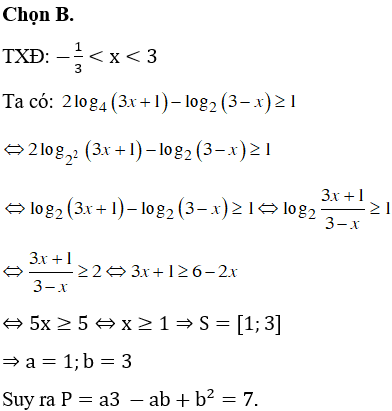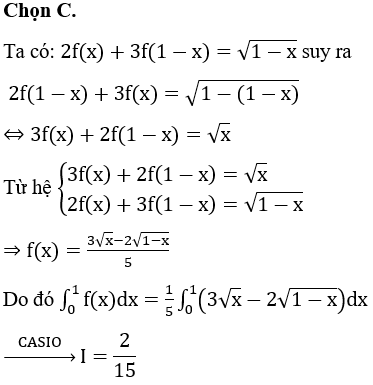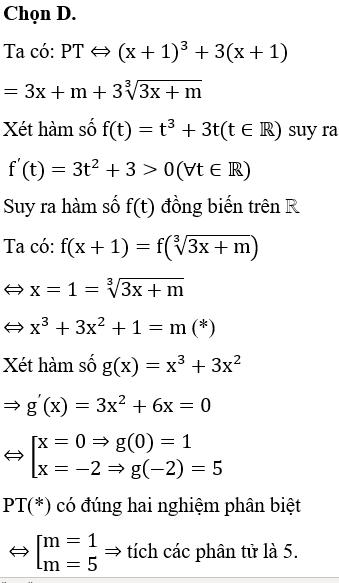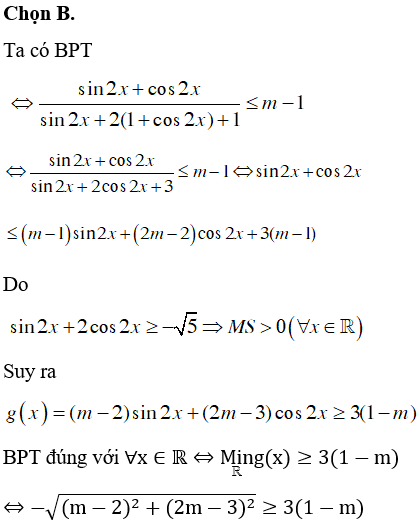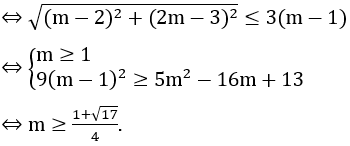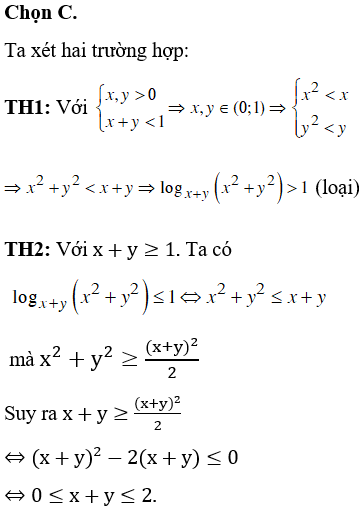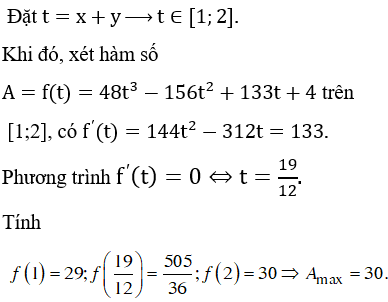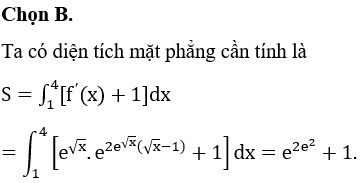50 câu hỏi trắc nghiệm thuộc ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN - đề 14

Câu 1:

Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình đường tròn?

A. $x^{2} + 2 y^{2} - 4 x - 8 y + 1 = 0 .$

B. $x^{2} + y^{2} - 4 x + 6 y - 12 = 0 .$

C. $x^{2} + y^{2} - 2 x - 8 y + 20 = 0 .$

D. $4 x^{2} + y^{2} - 10 x - 6 y - 2 = 0 .$

Xem đáp án

Câu 2:

Cho số phức z= -2+3i. Số phức liên hợp của z là:

A. $\bar{z} = - 2 - 3 i .$

B. $z = 2 - 3 i .$

C. $z = 3 - 2 i .$

D. $\bar{z} = \sqrt{13}$

Xem đáp án

Câu 3:

Cho hàm số y=f(x) có đạo hàm $f' (x) = x^{2} (x^{2} - 1)$ . Điểm cực tiểu của hàm số y=f(x) là:

A. x = 0.

B. x = -1.

C. y = 0.

D. x = 1

Xem đáp án

Câu 4:

Cho d: $\sqrt{3}$ x-y=0 và d': mx+y-1= 0. Giá trị của m để $\cos (d; d') = \frac{1}{2}$ là:

A. m = $\pm \sqrt{3}$

B. m = 0.

C. m= - $\sqrt{3}$ hoặc m= 0.

D. m= $\sqrt{3}$ hoặc m= 0.

Xem đáp án

Câu 5:

Cho hình phẳng D giới hạn bởi đường cong $y = \sqrt{2 - sinx}$ , trục hoành và các đường thẳng x=0, $x = \frac{π}{2}$ . Khối tròn xoay tạo thành D quay quanh trục hoành có thể tích V bằng:

A. $π - 1 .$

B. $π^{2} - 1 .$

C. $π (π - 1) .$

D. $π^{2} + 1 .$

Xem đáp án

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z+m= 0 (m là tham số) và mặt cầu (S): $(x - 2)^{2} + (y + 1)^{2} + z^{2} = 16$ . Tìm các giá trị của m để (P) cắt (S) theo giao tuyến là đường tròn có bán kính lớn nhất.

A. $- 1 - 4 \sqrt{3} \leq m \leq - 1 + 4 \sqrt{3} .$

B. $m \neq 0 .$

C. m =1.

D. m = -1

Xem đáp án

Câu 7:

Hai lực $\vec{F_{1}} và \vec{F_{2}}$ cùng tác động vào một vật tại điểm M. Biết cường độ của hai lực đều là 5 N và góc hợp bởi hai lực là 60^0. Cường độ hợp lực tác động lên vật là:

A. 10 $\sqrt{3}$ N.

B. 5 $\sqrt{3}$ N.

C. 20 N.

D. 20 $\sqrt{3}$ N.

Xem đáp án

Câu 8:

Trong không gian tọa độ Oxyz, cho hai điểm A(3;4;5),B(-1;0;1). Tìm tọa độ điểm M thỏa mãn $\vec{MA} + \vec{MB} = \vec{0}$

A. M(-4;-4;-4).

B. M(1;2;3).

C. M(2;4;6).

D. M(4;4;4).

Xem đáp án

Câu 9:

Cho hình trụ có diện tích xung quanh bằng 24 ${cm}^{2}$ , bán kính đường tròn đáy bằng 4 cm. Tính thể tích của khối trụ. x

A. 24 ${cm}^{3}$ .

B. 12 ${cm}^{3}$ .

C. 48 ${cm}^{3}$ .

D. 86 ${cm}^{3}$ .

Xem đáp án

Câu 10:

Cho tam giác ABC, lấy điểm M trên BC sao cho $\vec{MB} = 4 \vec{MC}$ . Chọn khẳng định đúng.

A. $\vec{AM} = \frac{1}{3} \vec{AB} - \frac{4}{3} \vec{AC}$

B. $\vec{AM} = \frac{4}{3} \vec{AB} - \frac{1}{3} \vec{AC}$

C. $\vec{AM} = - \frac{1}{3} \vec{AB} + \frac{4}{3} \vec{AC}$

D. $\vec{AM} = \frac{- 4}{3} \vec{AB} + \frac{1}{3} \vec{AC}$

Xem đáp án

Câu 11:

Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm số $y = tanx$ trục Ox, đường thẳng x = 0, đường thẳng x= $\frac{π}{3}$ quanh trục Ox là

A. $V = \sqrt{3} - \frac{π}{3}$

B. $V = \sqrt{3} + \frac{π}{3}$

C. $V = π \sqrt{3} + \frac{π^{2}}{3}$

D. $V = π \sqrt{3} - \frac{π^{2}}{3}$

Xem đáp án

Câu 12:

Biết $\lim \frac{{an}^{3} - 5 n^{2} + 1}{1 - 2 n^{3}} = - \frac{3}{2}$ với a là tham số. Lúc đó $a^{3} - a$ bằng:

A. 6

B. 27

C. 8

D. 24

Xem đáp án

Câu 13:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{x + \sqrt{3 x - 1}}{x^{2} - 1}$ là

A. 1.

B. 2.

C. 3

D. 4.

Xem đáp án

Câu 14:

Trong không gian Oxyz, cho điểm A(3;5;2). Phương trình đường thẳng nào dưới đây là phương trình của mặt phẳng đi qua các điểm là hình chiếu của điểm A trên các mặt phẳng tọa độ?

A. 10x+6y+15z-90= 0

B. 10x+6y+15z-60= 0

C.3x+5y+2z-60= 0

D. $\frac{x}{3} + \frac{y}{5} + \frac{z}{2} = 1$

Xem đáp án

Câu 15:

Cho hàm số y=f(x) có bảng biến thiên sau:

Số nghiệm của phương trình 4f(x)+3=0 là

A. 1

B. 2

C. 3.

D. 0

Xem đáp án

Câu 16:

Cho hình phẳng D giới hạn bởi đồ thị của hai hàm số y=f(x),y=g(x) (phần tô màu như hình vẽ). Gọi S là diện tích hình phẳng D. Mệnh đề nào dưới đây đúng?

A. $S = \int_{- 3}^{0} [f (x) - g (x)] dx .$

B. $S = \int_{- 3}^{0} [g (x) - f (x)] dx .$

C. $S = \int_{- 3}^{0} [f (x) + g (x)] dx .$

D. $S = \int_{- 3}^{1} [f (x) - g (x)]^{2} dx .$

Xem đáp án

Câu 17:

Trong không gian Oxyz, cho tam giác ABC biết C(1;1;1) và trong tâm G(2;5;8). Tìm tọa độ các đỉnh A và B thuộc mặt phẳng (Oxy) và B thuộc trục Oz

A. A(3;9;0) và B(0;0;15)

B. A(6;15;0) và B(0;0;24).

C. A(7;16;0) và B(0;0;25).

D. A(5;14;0) và B(0;0;23).

Xem đáp án

Câu 18:

Có 8 học sinh trong đó có 2 bạn tên A và B. Xếp ngẫu nhiên 8 học sinh trên theo một hàng ngang. Xác xuất để hai bạn A và B đứng cạnh nhau là

A. $\frac{1}{25}$

B. $\frac{5}{28}$

C. $\frac{1}{8}$

D. $\frac{1}{4}$

Xem đáp án

Câu 19:

Tính tổng T các nghiệm của phương trình ${(\log 10 x)}^{2} - 3 \log (100 x) = - 5$

A. T = 11

B. T = 12

C. T = 10

D. T = 110

Xem đáp án

Câu 20:

Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là 48. Trên các cạnh SA, SB, SC, SD lần lượt lấy các điểm A',B',C' và D' sao cho $\frac{SA'}{SA} = \frac{SC'}{SC} = \frac{1}{3}$ và $\frac{SB'}{SB} = \frac{SD'}{SD} = \frac{3}{4}$ . Tính thể tích V của khối đa diện lồi SA' B' C' D'.

A. V= 4.

B. V= 6.

C. V= 3/2.

D. V= 9.

Xem đáp án

Câu 21:

Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và $\int_{1}^{3} (x^{4} - 8 x) f (x) dx = 12 .$ Tính $I = \int_{1}^{3} (x^{3} - 2) F (x) dx .$

A. I= $\frac{147}{2}$

B. I= $\frac{147}{3}$

C. I= - $\frac{147}{2}$

D. I= 147.

Xem đáp án

Câu 22:

Cho hàm số y=f(x) có bảng biến thiên sau.

Hàm số y=f(x) nghịch biến trên khoảng nào sau đây

A. $(1; + \infty) .$

B. (-2;2).

C. (-2;0).

D. $(- \infty; 0) .$

Xem đáp án

Câu 23:

Cho số phức z thỏa mãn (1+i)z+(3-i) $\bar{z}$ =2-6i. Khẳng định nào sau đây đúng

A. z có phần thực và phần ảo đều dương.

B. z có phần thực và phần ảo đều âm

C. z có phần thực dương và phần ảo âm

D. z có phần thực âm và phần ảo dương.

Xem đáp án

Câu 24:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng (d): $\frac{x - 2}{2} = \frac{y + 2}{- 1} = \frac{z - 3}{1}$ . Gọi điểm B thuộc trục Ox sao cho AB vuông góc với đường thẳng (d). Khoảng cách từ B đến mặt phẳng ( $α$ ): 2x+2y-z-1=0 là:

A. 2

B. $\frac{2}{3}$

C. $\frac{1}{3}$

D. 1

Xem đáp án

Câu 25:

Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB = AC = 6, BC = 8. Khoảng cách từ O đến mặt phẳng (ABC) bằng 2. Thể tích khối cầu (S) bằng

A. $\frac{404 π}{5}$

B. $\frac{2916 π \sqrt{5}}{75} .$

C. $\frac{404 π \sqrt{505}}{75}$

D. $\frac{324 π}{5}$

Xem đáp án

Câu 26:

Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- $|z|$ (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?

A. x+y-2=0.

B. x-y+2=0.

C. x+y-1=0.

D. x+y+1=0.

Xem đáp án

Câu 27:

Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- $|z|$ (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?

A. x+y-2=0.

B. x-y+2=0.

C. x+y-1=0.

D. x+y+1=0.

Xem đáp án

Câu 28:

Cho hàm số $f (x) = x^{4} - 4 x^{3} + 2 x^{2} - x + 1$ ,∀ x∈ R. Tính $\int_{0}^{1} f^{2} (x) . f^{'} (x) dx$ .

A. $\frac{2}{3}$

B. 2.

C. - $\frac{2}{3}$

D. -2

Xem đáp án

Câu 29:

Bất phương trình $2 \log_{4} (3 x + 1) - \log_{2} (3 - x) \geq 1$ có tập nghiệm S = [a;b). Tính $P = a^{3} - ab + b^{2} .$

A. P = 43

B. P = 7

C. P = 23.

D. P =11

Xem đáp án

Câu 30:

Cho a,b,c∈R sao cho hàm số ${y=x}^{3} + {ax}^{2} + bx + c$ đạt cực trị tại x = 2 đồng thời có y(0)=1 và y(2)=-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây?

A. $(x - 1)^{2} + (y - 1)^{2} + (z - 1)^{2} = 16 .$

B. $(x - 2)^{2} + (y - 3)^{2} + (z + 5)^{2} = 64 .$

C. $x^{2} + y^{2} + (z + 5)^{2} = 36 .$

D. $(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 25 .$

Xem đáp án

Câu 31:

Xét hàm số f(x) liên tục trên đoạn [0;1] và thỏa mãn 2f(x)+3f(1-x)= $\sqrt{1 - x}$ . Giá trị của tích phân $\int_{0}^{1} f (x) dx$ bằng:

A. $\frac{2}{3}$

B. $\frac{1}{6}$

C. $\frac{2}{15}$

D. $\frac{3}{5}$

Xem đáp án

Câu 32:

Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(-1;0;1),B(3;2;1),C(5;3;7). Gọi M(a;b;c) là điểm thỏa mãn MA = MB và MB + MC đạt giá trị nhỏ nhất. Tìm P=a+b+c ?

A. P = 4.

B. P = 0

C. P = 2

D. P = 5

Xem đáp án

Câu 33:

Xét bất phương trình $\log_{2}^{2} 2 x - 2 (m + 1) \log_{2} x - 2 < 0$ .Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng $(\sqrt{2}; + \infty)$ .

A. $m \in (- \infty; 0) .$

B. $m \in (- \frac{3}{4}; 0) .$

C. $m \in (- \frac{3}{4}; 0) .$

D. $m \in (0; + \infty) .$

Xem đáp án

Câu 34:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a, tam giác SAB và tam giác SCB lần lượt vuông tại A, C. Khoảng cách từ S đến mặt phẳng (ABC) bằng 2a. Cosin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng:

A. $\frac{1}{3}$

B. $\frac{1}{\sqrt{3}}$

C. $\frac{1}{\sqrt{2}}$

D. $\frac{1}{2}$

Xem đáp án

Câu 35:

Với hai số phức $z_{1} và z_{2}$ thỏa mãn $z_{1} + z_{2} = 8 + 6 i$ và $|z_{1} - z_{2}| = 2$ . Tim giá trị lớn nhất của biểu thức $P = | z_{1} | + | z_{2} |$ .

A. P=4 $\sqrt{6}$

B. P=2 $\sqrt{26}$

C. P=5+3 $\sqrt{5}$

D. P=34+3 $\sqrt{2}$

Xem đáp án

Câu 36:

Gọi S là tập hợp các giá trị thực của tham số m sao cho phương trình $(x + 1)^{3} + 3 - m = 3 \sqrt[3]{3 x + m}$ có đúng nghiệm thực. Tích tất cả các phần tử của tập hợp S là

A. -1

B. 1

C. 3

D. 5

Xem đáp án

Câu 37:

Cho hình lăng trụ đứng ABC.A' B' C' có AB=AC=a, góc $∠ BAC = 120^{0}, AA' = a$ .Gọi M, N lần lượt là trung điểm của B^' C^' và CC^'. Số đo góc giữa mặt phẳng (AMN) và mặt phẳng (ABC) bằng:

A. $60^{0}$

B. $30^{0}$

C. $\arcsin \frac{\sqrt{3}}{4}$

D. $arccos \frac{\sqrt{3}}{4}$

Xem đáp án

Câu 38:

Tìm tất cả các giá trị tham số m để hàm số $y = |\frac{x^{2} + (2 - m) x - m + 2}{x + 1}|$ có 4 cực trị.

A. $- 2 \leq m \leq 3 .$

B. $- 2 < m \leq 3 .$

C. m> 2 hoặc m< -2

D. m> 2 hoặc m< -3

Xem đáp án

Câu 39:

Trong không gian Oxyz, cho đường thẳng d: $\frac{x - 3}{2} = \frac{y + 2}{1} = \frac{z + 1}{- 1}$ và mặt phẳng có phương trình (P): x+y+z+2=0. Đường thẳng $Δ$ nằm trong mặt phẳng (P), vuông góc với đường thẳng d đồng thời khoảng cách từ giao điểm I của d với (P) đến $Δ$ bằng $\sqrt{42}$ . Gọi M(5;b;c) là hình chiếu vuông góc của I trên $Δ$ . Giá trị của bc bằng:

A. -10.

B. 10

C. 12

D. -20

Xem đáp án

Câu 40:

Tìm tất cả các giá trị thực của m để bất phương trình $\frac{2 sinxcosx + \cos 2 x}{\sin 2 x + 4 \cos^{2} x + 1} \leq m - 1$ đúng với mọi x $\in R$ .

A. $m \geq \frac{- 3 + \sqrt{17}}{4}$ .

B. $m \geq \frac{1 + \sqrt{17}}{4}$

C. $m \leq \frac{1 - \sqrt{17}}{4}$ .

D. $m \leq \frac{- 3 + \sqrt{17}}{4}$

Xem đáp án

Câu 41:

cho dãy số $(u_{n}) : \{\begin{cases} u_{1} = 2 \\ u_{n + 1} = u_{n} = 2 n, \forall n \in N^{*} \end{cases}$ . Bắt đầu từ số hạng thứ bao nhiêu thì $u_{n}$ có nhiều hơn 4 chữ số

A. 200

B. 101

C. 100

D. 201.

Xem đáp án

Câu 42:

Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên, mỗi số gồm sáu chữ số đôi một khác nhau sao cho tổng của ba chữ số đầu và tổng của ba chữ số cuối kém nhau một đơn vị

A. 108 số.

B. 72 số.

C. 423 số

D. 216 số

Xem đáp án

Câu 43:

Cho hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức: $\{\begin{cases} f (1) + g (1) = 4 \\ g (x) = - x . f' (x); f (x) = - x . g' (x) \end{cases}$ . Tính tích phân $\int_{1}^{4} [f (x) + g (x)] dx$

A. 8ln2.

B. 3ln2

C. 6ln2

D. 4ln2

Xem đáp án

Câu 44:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(α) : bc . x + ac . y + ab . z - abc = 0$ với a, b, c là các số khác 0 thỏa mãn $\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7$ . Gọi A, B, C lần lượt là giao điểm của $(α)$ với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng $(α)$ tiếp xúc với mặt cầu (S): $(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = \frac{72}{7}$ . Thể tích khối OABC với O là gốc tọa độ bằng

A. $\frac{2}{9}$

B. $\frac{3}{4}$

C. $\frac{1}{8}$

D. $\frac{4}{3}$

Xem đáp án

Câu 45:

Tìm tất cả các giá trị của m để phương trình $\sin^{4} x + \cos^{4} x + \cos^{2} 4 x = m$ có 4 nghiệm phân biệt thuộc đoạn $[\frac{- π}{4}; \frac{π}{4}]$ .

A. $m \leq \frac{47}{64} hoặc m \geq \frac{3}{2}$

B. $\frac{47}{64} < m < \frac{3}{2}$

C. $\frac{47}{64} < m \leq \frac{3}{2}$

D. $\frac{47}{64} \leq m \leq \frac{3}{2}$

Xem đáp án

Câu 46:

Cho các số thực dương x, y thỏa mãn $\log_{x + y} (x^{2} + y^{2}) \leq 1$ .Giá trị lớn nhất của biểu thức A= $48 (x + y)^{3} - 156 (x + y)^{2} + 133 (x + y) + 4$ là

A. 29.

B. 1369/36.

C. 30.

D. 505/36

Xem đáp án

Câu 47:

Cho đa giác đều 100 đỉnh. Chọn ngẫu nhiên 3 đỉnh của đa giác. Xác suất để 3 đỉnh đỉnh được chọn là 3 đỉnh của một tam giác tù là

A. $\frac{3}{11}$

B. $\frac{16}{33}$

C. $\frac{8}{11}$

D. $\frac{4}{11}$

Xem đáp án

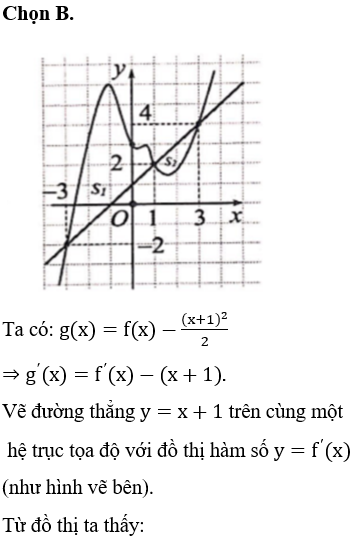
Chọn C.

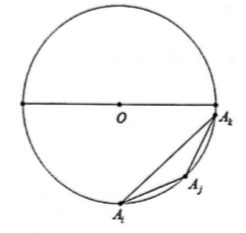
Gọi đa giác đều là A₁A₂..A₁₀₀ và O là tâm đường tròn ngoại tiếp tam giác đã cho.

Chọn 3 điểm bất kì ta được 1 tam giác suy ra có: $C_{100}^{3}$ tam giác.

Chia 100 đỉnh thành 2 phần thuộc 2 nửa đường tròn khác nhau

Bước 1: Chọn 1 đỉnh có 100 cách chọn.

Bước 2: Chọn 2 đỉnh còn lại để tạo thành 3 đỉnh của tam giác A_iA_jA_k tù thì 2 đỉnh này phải nằm trên 1 nửa đường trò đã chia.

Như vậy có: $100 . C_{49}^{2}$ cách chọn.

Do đó xác xuất cần tìm là: $\frac{100 . C_{49}^{2}}{C_{100}^{2}} = \frac{8}{11}$

Câu 48:

Cho hàm số f(x) luôn dương và có đạo hàm liên tục trên đoạn [1;4]. Biết rằng $f' (x) = e^{\sqrt{x}} f (x)$ , ∀ x∈ [1;4] và f(1)=1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f' (x)=1, trục hoành và hai đường thẳng x=1,x=4.

A. $e^{e^{2}} + 1 .$

B. $e^{2 e^{2}} + 1 .$

C. $e^{2 e^{2}} + 2 .$

D. $e^{e^{2}} + 2 .$

Xem đáp án

Câu 49:

Từ 9 học sinh gồm 4 học sinh giỏi, 3 học sinh khác, 2 học sinh trung bình, giáo viên muốn thành lập 3 nhóm làm 3 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.

A. $\frac{3}{70}$

B. $\frac{6}{35}$

C. $\frac{9}{35}$

D. $\frac{18}{35}$

Xem đáp án

Chọn C.

Số phần tử của không gian mẫu là $n (Ω) = C_{9}^{3} . C_{6}^{3} . C_{3}^{3} .$

Gọi X là biến cố “nhóm nào cũng có học sinh giỏi và học sinh khá”

Khi đó, ta xét các chia nhóm như sau:

· N1: 2 học sinh giỏi, 1 học sinh khá.

· N2: 1 học sinh giỏi, 1 học sinh khá và

· 1 học sinh trung bình.

· N3: 1 học sing giỏi, 1 học sinh khá

· và 1 học sinh trung bình.

Suy ra có $3 . (C_{4}^{2} . C_{3}^{1}) . C_{2}^{1} . C_{2}^{1} . C_{2}^{1}$ cách chia $\Rightarrow n (X) = 3 . C_{4}^{2} . C_{3}^{1} . C_{2}^{1} . C_{2}^{1} . C_{2}^{1} .$

Vậy xác suất cần tính là $P = \frac{n (X)}{n (Ω)} = \frac{9}{35}$

Câu 50:

Cho hàm số y=f(x) có đạo hàm, liên tục trên đoạn [-3;3] và đồ thị hàm số y=f' (x) như hình vẽ bên. Biết f(1)=6 và g(x)=f(x)- $\frac{(x + 1)^{2}}{2}$ .

Kết luận nào sau đây là đúng

A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].

B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].

C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].

D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN

ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN - đề 14

Danh sách câu hỏi

Bài thi liên quan