(2023) Đề thi thử Vật Lí Sở GD Bình Thuận có đáp án
-
151 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Một vật khối lượng m dao động điều hòa theo phương trình \(x = A\cos (\omega t + \varphi )\). Mốc thế năng tại vị trí cân bằng. Cơ năng của vật bằng thế năng tại vị trí
Xem đáp án
\(W = \frac{1}{2}k{A^2}\). Chọn D
Câu 2:
Một sóng cơ hình sin lan truyền trong một môi trường với bước sóng λ. Quãng đường mà sóng truyền được trong một chu kì là
Xem đáp án
Chọn D
Câu 3:
“Năng lượng của sóng âm truyền qua một đơn vị diện tích được đặt vuông góc với phương truyền âm trong một đơn vị thời gian” là định nghĩa của đại lượng
Xem đáp án
\(I = \frac{P}{S}\). Chọn C
Câu 5:
Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do, điện tích của một bản tụ điện tại thời điểm t có dạng \(q = {q_0}\cos \left( {\omega t} \right)\). Khi đó, cường độ dòng điện trong mạch sẽ có biểu thức là
Xem đáp án
Chọn C
Câu 6:
Đặt điện áp xoay chiều có tần số góc ω vào hai đầu cuộn cảm thuần có độ tự cảm L. Cảm kháng là
Xem đáp án
\({Z_L} = \omega L\). Chọn B
Câu 8:
Đặt điện áp xoay chiều \(u = U\sqrt 2 \cos \omega {\rm{t (V)}}\) vào hai đầu một đoạn mạch có R, L, C mắc nối tiếp. Điện áp hiệu dụng hai đầu các phần tử R, L, C lần lượt là \({U_R},{U_L},{U_C}\). Công thức nào sau đây đúng?
Xem đáp án
Chọn D
Câu 9:
Chiếu một chùm sáng đơn sắc hẹp màu đỏ vào mặt bên của lăng kính đặt trong không khí. Khi đi qua lăng kính, chùm tia sáng này sẽ
Xem đáp án
Chọn D
Câu 10:
Kí hiệu của hạt nhân \(X\)gồm có 13 prôtôn và 14 nơtron là
Xem đáp án
\(A = Z + N = 13 + 14 = 27\). Chọn A
Câu 11:
Cho các sóng điện từ sau: sóng vô tuyến, tia hồng ngoại, tia tử ngoại, tia sáng màu lục. Tia nào có bước sóng nhỏ nhất?
Xem đáp án
Chọn B
Câu 14:
Một con lắc lò xo gồm lò xo có độ cứng k và vật khối lượng m, dao động điều hòa với chu kì T là
Xem đáp án
\(T = 2\pi \sqrt {\frac{m}{k}} \). Chọn C
Câu 15:
Trong nguyên tử hiđrô, với r0 là bán kính Bo thì bán kính ở quỹ đạo dừng thứ n là
Xem đáp án
Chọn B
Câu 16:
Xem đáp án
Chọn C
Câu 18:
Trong dao động cưỡng bức, khi xảy ra hiện tượng cộng hưởng thì đại lượng nào sau đây đạt đến giá trị cực đại?
Xem đáp án
Chọn C
Câu 20:
Cho hai dao động điều hòa cùng phương, cùng tần số, có độ lệch pha \(\Delta \varphi = (2k + 1)\pi \) với \(k = 0, \pm 1, \pm 2,...\)Mối quan hệ về pha của hai dao động này là
Xem đáp án
Chọn D
Câu 21:
Một sóng dừng trên dây có khoảng cách giữa hai nút sóng gần nhau nhất là \(2\;{\rm{cm}}\). Bước sóng có giá trị là
Xem đáp án
\(\frac{\lambda }{2} = 2 \Rightarrow \lambda = 4cm\). Chọn B
Câu 22:
Mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 1 mH và tụ điện có điện dung 1000 pF. Dao động điện từ của mạch có tần số góc
Xem đáp án
\(\omega = \frac{1}{{\sqrt {LC} }} = \frac{1}{{\sqrt {{{10}^{ - 3}}{{.1000.10}^{ - 12}}} }} = {10^6}\) (rad/s). Chọn A
Câu 23:
Đoạn mạch xoay chiều chứa 2 phần tử tụ điện và điện trở. Gọi φ là độ lệch pha giữa điện áp và cường độ dòng điện, kết luận nào sau đây đúng?
Xem đáp án
Chọn C
Câu 24:
Một đoạn mạch xoay chiều có R, L, C mắc nối tiếp, gồm có điện trở thuần\(50\Omega \), cảm kháng\(70\Omega \)và dung kháng \(100\Omega \). Hệ số công suất của đoạn mạch là
Xem đáp án
\(\cos \varphi = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{50}}{{\sqrt {{{50}^2} + {{\left( {70 - 100} \right)}^2}} }} \approx 0,857\). Chọn D
Câu 25:
Một sóng ngang truyền trên trục Ox được mô tả bởi phương trình \(u = A\cos \left( {\omega t - \frac{{2\pi x}}{\lambda }} \right)\) trong đó x, u được đo bằng cm và t đo bằng s. Tốc độ truyền sóng được tính bằng
Xem đáp án
\(v = \lambda .\frac{\omega }{{2\pi }}\). Chọn C
Câu 26:
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe hẹp là 0,15 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 60 cm. Ánh sáng chiếu vào hai khe có bước sóng 0,75 µm. Khoảng cách từ vân sáng trung tâm đến vân sáng bậc 4 là
Xem đáp án
\(i = \frac{{\lambda D}}{a} = \frac{{0,75.0,6}}{{0,15}} = 3mm\)
\(x = ki = 4.3 = 12mm\). Chọn D
Câu 27:
Biết năng lượng liên kết của hạt nhân \({}_{26}^{56}Fe\)là 492,24 MeV và 1u = 931,5 MeV/c2. Độ hụt khối của hạt nhân\({}_{26}^{56}Fe\)gần đúng bằng
Xem đáp án
\({W_{lk}} = \Delta m{c^2} \Rightarrow 492,24 = \Delta m.931,5 \Rightarrow \Delta m \approx 0,5284u\). Chọn D
Câu 28:
Một con lắc đơn có chiều dài \(\ell \) dao động điều hòa tại nơi có gia tốc trọng trường g. Quả nặng có khối lượng m thì tần số góc là ω. Thay quả nặng khác có khối lượng 4m thì tần số góc là
Xem đáp án
\(\omega = \sqrt {\frac{g}{l}} \) không đổi. Chọn A
Câu 29:
Cho điện tích điểm \[Q{\rm{ }} = {\rm{ }}{6.10^{ - 8}}C\] và hệ số tỉ lệ \(k = {9.10^9}\frac{{N.{m^2}}}{{{C^2}}}\). Cường độ điện trường do Q gây ra tại một điểm cách nó 5cm trong chân không là
Xem đáp án
\(E = k.\frac{Q}{{{r^2}}} = {9.10^9}.\frac{{{{6.10}^{ - 8}}}}{{0,{{05}^2}}} = 216000\) (V/m). Chọn D
Câu 30:
Công thoát êlectron ra khỏi một kim loại là 3,45 eV. Cho biết 1eV = 1,6.10-19J, hằng số Plăng h = 6,625.10-34J.s, tốc độ ánh sáng trong chân không c = 3.108m/s. Giới hạn quang điện của kim loại này là
Xem đáp án
\(\varepsilon = \frac{{hc}}{\lambda } \Rightarrow 3,45.1,{6.10^{ - 19}} = \frac{{1,{{9875.10}^{ - 25}}}}{\lambda } \Rightarrow \lambda = 0,{36.10^{ - 6}}m = 0,36\mu m\). Chọn A
Câu 31:
Xem đáp án
\({P_{MB}} = 2{P_{AN}} \Rightarrow {I^2}\left( {R + r} \right) = 2{I^2}r \Rightarrow R = r = 1\) (chuẩn hóa)
\({U_{AN}} = {U_{MB}} \Rightarrow {Z_{AN}} = {Z_{MB}} = x\)
\[{u_{AN}} \bot {u_{MB}} \Rightarrow {\cos ^2}{\varphi _{AN}} + {\cos ^2}{\varphi _{MB}} = 1 \Rightarrow {\left( {\frac{R}{{{Z_{AN}}}}} \right)^2} + {\left( {\frac{{R + r}}{{{Z_{MB}}}}} \right)^2} = 1 \Rightarrow {\left( {\frac{1}{x}} \right)^2} + {\left( {\frac{2}{x}} \right)^2} = 1 \Rightarrow x = \sqrt 5 \]
\(Z_{MB}^2 = {\left( {R + r} \right)^2} + Z_L^2 \Rightarrow 5 = {2^2} + Z_L^2 \Rightarrow {Z_L} = 1\)
\(Z_{AN}^2 = {r^2} + Z_{LC}^2 \Rightarrow 5 = 1{}^2 + Z_{LC}^2 \Rightarrow {Z_{LC}} = 2\)
\({U_{MN}} = \frac{{U\sqrt {{r^2} + Z_L^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + Z_{LC}^2} }} = \frac{{\frac{{250}}{{\sqrt 2 }}.\sqrt {{1^2} + {1^2}} }}{{\sqrt {{2^2} + {2^2}} }} = \frac{{125}}{{\sqrt 2 }}V\). Chọn A
Câu 32:
Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm A và B cách nhau 21cm, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng \(\lambda = 8{\rm{cm}}\). Điểm M trên mặt nước thuộc đường trung trực của AB, gần A nhất và dao động cùng pha với A. Điểm N trên mặt nước gần A nhất mà phần tử nước tại đó dao động với biên độ cực đại và cùng pha với A. Khoảng cách nhỏ nhất giữa M và N gần nhất với giá trị nào sau đây?
Xem đáp án
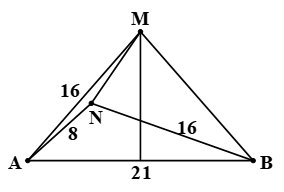
\(MA = k\lambda = 8k > \frac{{AB}}{2} = 10,5 \to {k_{\min }} = 2 \to MA = 8.2 = 16cm\)
N là cực đại cùng pha gần A nhất \( \Rightarrow NA = \lambda = 8cm\)
N gần M nhất \( \Rightarrow NB - NA = \lambda \Rightarrow NB - 8 = 8 \Rightarrow NB = 16cm\)
\(\widehat {MAN} = \widehat {MAB} - \widehat {NAB} = \arccos \frac{{10,5}}{{16}} - \arccos \frac{{{{21}^2} + {8^2} - {{16}^2}}}{{2.21.8}} = 6,{81^o}\)
\(MN = \sqrt {{{16}^2} + {8^2} - 2.16.8.\cos 6,{{81}^o}} \approx 8,1cm\). Chọn C
Câu 33:
Thí nghiệm Y-âng về giao thoa với 3 ánh sáng đơn sắc gồm: λ1 = 0,4 μm (tím), λ2 = 0,48 μm (lam), λ3 = 0,72 μm (đỏ). Giữa hai vân sáng liên tiếp có màu giống như màu của vân sáng trung tâm, số vân sáng khác màu 3 ánh sáng đơn sắc trên là
Xem đáp án
\(\frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{0,4}}{{0,48}} = \frac{5}{6} \Rightarrow {\lambda _{12}} = 2,4\)
\(\frac{{{\lambda _1}}}{{{\lambda _3}}} = \frac{{0,4}}{{0,72}} = \frac{5}{9} \Rightarrow {\lambda _{13}} = 3,6\)
\(\frac{{{\lambda _2}}}{{{\lambda _3}}} = \frac{{0,48}}{{0,72}} = \frac{2}{3} \Rightarrow {\lambda _{13}} = 1,44\)
\(\frac{{{\lambda _1}}}{{{\lambda _{23}}}} = \frac{{0,4}}{{1,44}} = \frac{5}{{18}} \Rightarrow {\lambda _{123}} = 7,2 = 3{\lambda _{12}} = 2{\lambda _{12}} = 5{\lambda _{23}}\)
\({N_{kds}} = {N_{12}} + {N_{13}} + {N_{23}} = \left( {3 - 1} \right) + \left( {2 - 1} \right) + \left( {5 - 1} \right) = 7\). Chọn D
Câu 34:
Nguyên tử hiđrô ở trạng thái cơ bản có mức năng lượng \( - 13,6eV\). Để chuyển lên trạng thái dừng có mức năng lượng \({E_n}\)thì nguyên tử hiđrô phải hấp thụ một phôtôn có bước sóng \(94nm\). Sau đó từ trạng thái dừng có mức năng lượng\({E_n}\)về trạng thái dừng có mức năng lượng \( - 3,4eV\) thì nguyên tử hiđrô phát ra phôtôn có bước sóng λ. Cho biết 1eV = 1,6.10-19J, hằng số Plăng h = 6,625.10-34J.s, tốc độ ánh sáng trong chân không c = 3.108m/s. Giá trị λ bằng
Xem đáp án
\(\left\{ \begin{array}{l}\frac{{hc}}{{{\lambda _1}}} = {E_n} - {E_1}\\\frac{{hc}}{{{\lambda _2}}} = {E_n} - {E_2}\end{array} \right. \Rightarrow \frac{{hc}}{{{\lambda _1}}} - \frac{{hc}}{{{\lambda _2}}} = {E_2} - {E_1}\)
\( \Rightarrow 1,{9875.10^{ - 25}}\left( {\frac{1}{{{{94.10}^{ - 9}}}} - \frac{1}{{{\lambda _2}}}} \right) = \left( { - 3,4 + 13,6} \right).1,{6.10^{ - 19}} \Rightarrow {\lambda _2} \approx {412.10^{ - 9}}m = 412nm\). Chọn D
Câu 35:
Một máy biến áp lí tưởng cung cấp công suất\({\rm{3,3kW}}\)dưới một điện áp hiệu dụng \(220\;{\rm{V}}\). Biến áp nối với đường dây tải điện có tổng trở \(2\Omega \). Điện áp hiệu dụng ở cuối đường dây tải điện
Xem đáp án
\(I = \frac{P}{U} = \frac{{3300}}{{220}} = 15A\)
\(\Delta U = IR = 15.2 = 30V\)
\({U_{tt}} = U - \Delta U = 220 - 30 = 190V\). Chọn C
Câu 36:
\(_{84}^{210}Po\) là chất phóng xạ có chu kỳ bán rã 138 ngày và có phương trình phân rã là \(_{84}^{210}Po \to \alpha \; + \;_{82}^{206}Pb\). Ban đầu có 2 gam \(_{84}^{210}Po\)nguyên chất, sau 276 ngày thì khối lượng\(_{82}^{206}Pb\)được tạo ra là
Xem đáp án
\(\Delta N = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \frac{{{m_{Pb}}}}{{{A_{Pb}}}} = \frac{{{m_{Po}}}}{{{A_{Po}}}}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \frac{{{m_{Pb}}}}{{206}} = \frac{2}{{210}}.\left( {1 - {2^{\frac{{ - 276}}{{138}}}}} \right) \Rightarrow {m_{Pb}} \approx 1,47g\). Chọn D
Câu 37:
Đặt điện áp xoay chiều \(u = 60\sqrt 2 \cos (\omega t + \varphi )\,\,\,(V)\) (\(\omega \) thay đổi được) vào hai đầu đoạn mạch AB có R, L, C mắc nối tiếp, cho R =\(30\Omega \). Khi \(\omega = 200({\rm{rad}}/{\rm{s}})\) thì cường độ dòng điện hiệu dụng trong mạch đạt giá trị cực đại và điện áp hiệu dụng giữa hai đầu tụ điện là \(100\;{\rm{V}}\). Hệ số tự cảm của cuộn dây là
Xem đáp án
\({I_{\max }} \to \)cộng hưởng \( \Rightarrow {U_C} = {U_L} = \frac{{U{Z_L}}}{R} \Rightarrow 100 = \frac{{60.{Z_L}}}{{30}} \Rightarrow {Z_L} = 50\Omega \)
\(L = \frac{{{Z_L}}}{\omega } = \frac{{50}}{{200}} = 0,25H\). Chọn A
Câu 38:
Trên một sợi dây đàn hồi nằm ngang đang có sóng dừng, tốc độ truyền sóng không đổi. Khi hai đầu dây cố định và tần số sóng trên dây là \(56\;{\rm{Hz}}\), ta thấy trên dây có 4 điểm bụng. Nếu một đầu dây cố định, đầu còn lại thả tự do, ta thấy trên dây có 7 điểm nút thì tần số sóng trên dây là
Xem đáp án
\(l = k.\frac{\lambda }{2} = k.\frac{v}{{2f}} \Rightarrow \frac{k}{f} = const \Rightarrow \frac{4}{{56}} = \frac{{6,5}}{f} \Rightarrow f = 91Hz\). Chọn B
Câu 39:
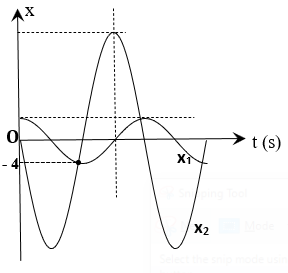
Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng phương cùng chu kì T mà đồ thị li độ \({x_1}\)và \({x_2}\) phụ thuộc vào thời gian như hình vẽ. Biết \({x_2} = {v_1}\frac{T}{2}\), tốc độ cực đại của chất điểm là 32,5 cm/s. Chu kì T gần giá trị nào nhất
Xem đáp án
\({x_{2\max }} = {v_{1\max }}.\frac{T}{2} \Rightarrow {A_2} = \omega {A_1}.\frac{{2\pi }}{{2\omega }} \Rightarrow {A_2} = \pi {A_1}\)
Vuông pha \( \Rightarrow {\left( {\frac{{{x_1}}}{{{A_1}}}} \right)^2} + {\left( {\frac{{{x_2}}}{{{A_2}}}} \right)^2} = 1 \Rightarrow {\left( {\frac{4}{{{A_1}}}} \right)^2} + {\left( {\frac{4}{{\pi {A_1}}}} \right)^2} = 1 \Rightarrow {A_1} \approx 4,198cm\)
\(\omega = \frac{{{v_{\max }}}}{A} = \frac{{{v_{\max }}}}{{\sqrt {A_1^2 + A_2^2} }} = \frac{{32,5}}{{\sqrt {{\pi ^2} + 1} {A_1}}} \approx 2,348rad/s \to T = \frac{{2\pi }}{\omega } \approx 2,68s\). Chọn C
Câu 40:
Một con lắc lò xo gồm quả cầu nhỏ khối lượng \(200\;{\rm{g}}\) và lò xo có độ cứng \(50\;N/m\). Cho con lắc dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là \(50\)cm/s thì gia tốc của nó là \(\sqrt 3 {\pi ^2}{\rm{ m/}}{{\rm{s}}^2}\), lấy π2 = 10. Cơ năng của con lắc là
Xem đáp án
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{50}}{{0,2}}} = 5\sqrt {10} \approx 5\pi \) (rad/s)
\(a = - {\omega ^2}x \Rightarrow \sqrt 3 {\pi ^2} = - {\left( {5\pi } \right)^2}x \Rightarrow x = - 0,04\sqrt 3 m = - 4\sqrt 3 cm\)
\(A = \sqrt {{x^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} = \sqrt {{{\left( { - 4\sqrt 3 } \right)}^2} + {{\left( {\frac{{50}}{{5\sqrt {10} }}} \right)}^2}} = \sqrt {58} \) (cm)
\(W = \frac{1}{2}k{A^2} = \frac{1}{2}.50.{\left( {\frac{{\sqrt {58} }}{{100}}} \right)^2} = 0,145J\). Chọn C