Bài tập chuyên đề Toán 11 Bài 1: Vecto trong không gian - Hai đường thẳng vuông góc có đáp án
Chủ đề 1: Vectơ trong không gian
-
575 lượt thi
-
48 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng
 Xem đáp án
Xem đáp án
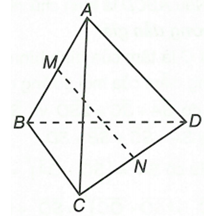
Ta có
(đẳng thức này đúng).
Do M, N lần lượt là trung điểm các cạnh AB và CD
nên
Do đó
Vậy
Câu 2:
Cho hình hộp ABCD.A'B'C'D'. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của vectơ.
a) Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ
 Xem đáp án
Xem đáp án
a) Ta có
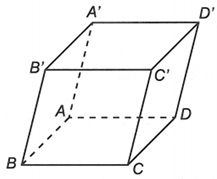
+)
+)
+)
+)
Câu 3:
Hãy kể tên các vectơ luôn có độ dài bằng nhau và bằng độ dài của vectơ .
 Xem đáp án
Xem đáp án
Từ tính chất của hình bình hành, ta suy ra các vectơ luôn có độ dài bằng độ dài của vectơ là
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Chứng minh
 Xem đáp án
Xem đáp án
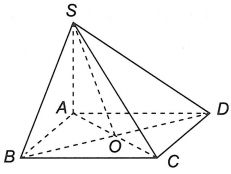
a) Gọi O là tâm của hình bình hành ABCD thì O là trung điểm của mỗi đường chéo AC và BD.
Do đó và
Vậy
Câu 5:
 Xem đáp án
Xem đáp án
b) Ta có ,
Suy ra
(vì và là hai vectơ đối nhau nên )
Tương tự
Mà ABCD là hình chữ nhật nên OA = OB
Suy ra
Câu 6:
Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho . Chứng minh ba vectơ đồng phẳng.
 Xem đáp án
Xem đáp án
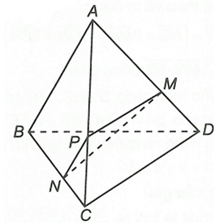
Ta có
Cộng vế theo vế của hai đẳng thức này ta được
Do nên
Vậy đồng phẳng.
Câu 7:
Cho hình lăng trụ tam giác ABC.A'B'C' có . Hãy phân tích các vectơ qua các vectơ .
 Xem đáp án
Xem đáp án
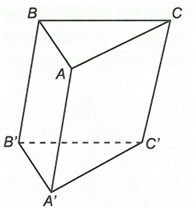
Ta có
Câu 8:
Cho hình chóp S.ABC. Lấy điểm M và N sao cho và . Chứng minh rằng ba vectơ đồng phẳng.
 Xem đáp án
Xem đáp án
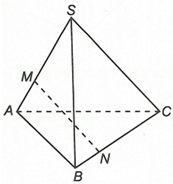
Từ giả thiết ta có
Lại có
Cộng vế theo vế ta được
Vậy đồng phẳng.
Câu 9:
Cho hình chóp S.ABC. Lấy các điểm A', B', C' lần lượt thuộc các tia SA, Sb, SC sao cho , trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A'B'C' đi qua trọng tâm của tam giác ABC khi và chỉ khi .
 Xem đáp án
Xem đáp án
Từ giả thiết ta suy ra
Gọi G là trọng tâm của tam giác . Ta có
với
với
(do không đồng phẳng)
+) Nếu ta có (với ).
Do đó
+) Nếu , ta đặt thì
và
Do đó
Câu 10:
 Xem đáp án
Xem đáp án
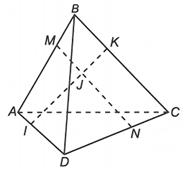
Ta có nên với điểm O bất kỳ thì
Tương tự, ta chỉ ra được
Ta có
Suy ra
Suy ra I, J, K thẳng hàng.
Câu 11:
Cho hình hộp ABCD.A'B'C'D'. Gọi G, G' lần lượt là trọng tâm của các tam giác . Chứng minh các điểm thẳng hàng.
 Xem đáp án
Xem đáp án
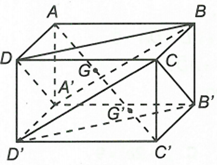
Đặt
Ta có (quy tắc hình hộp).
Theo quy tắc trọng tâm, ta có
Vậy nên các điểm thẳng hàng.
Câu 12:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Với ABC là tam giác đều ta có nhưng và nên B sai.
Câu 13:
Trong không gian cho ba vectơ . Cho các khẳng định sau.
(1) Nếu các vectơ đồng phẳng thì các vectơ thuộc một mặt phẳng nào đó.
(2) Nếu các vectơ đồng phẳng thì ba vectơ cùng phương.
(3) Nếu tồn tại hai số thực m, n sao cho thì các vectơ đồng phẳng.
(4) Nếu các vectơ đồng phẳng thì giá của chúng song song với mặt phẳng nào đó.
Có bao nhiêu khẳng định đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Khẳng định (1) sai vì khi đồng phẳng thì giá của chúng luôn song song với mặt mặt phẳng.
Khẳng định (2) sai vì các vectơ đồng phẳng không yêu cầu là phải cùng phương.
Khẳng định (3) và (4) đúng theo điều kiện và định nghĩa ba vectơ đồng phẳng.
Câu 14:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Vậy
Câu 15:
 Xem đáp án
Xem đáp án
Chọn đáp án D
A sai vì
B sai vì
C sai vì
D đúng vì (đúng)
Câu 16:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có . Từ đó phương án A sai.
Ta có . Từ đó phương án B sai.
Ta có đồng phẳng đồng phẳng (C đúng).
Phương án D sai vì nếu B là trung điểm của đoạn thẳng AC thì mà .
Câu 17:
 Xem đáp án
Xem đáp án
Chọn đáp án A
+) là hình bình hành (A đúng).
+) ta phải suy ra tứ giác ABDC là hình bình hành chứ không phải ABCD (B sai).
+) C sai vì đúng với mọi vị trí của A, B, C, D .
+) D sai vì với thì AD là đường chéo của hình bình hành ABCD.
Câu 18:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có:
Suy ra
Câu 19:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có O là trọng tâm tam giác nên (1)
Ta có:
Từ (1) suy ra
Suy ra (2)
Mà (3)
Từ (2) và (3) suy ra
Câu 20:
 Xem đáp án
Xem đáp án
Chọn đáp án C
C sai vì chỉ cần ba vectơ có giá cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.
Câu 21:
 Xem đáp án
Xem đáp án
Chọn đáp án C
A, B sai vì và thẳng hàng mà O là điểm bất kì.
C đúng vì
D sai vì là hình bình hành. Khi đó .
Câu 22:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có:
Câu 23:
 Xem đáp án
Xem đáp án
Chọn đáp án D
A sai khi có giá cùng nằm trong (P), còn có giá song song với (P)
B sai với ba vectơ ta có thì đồng phẳng nhưng chỉ đúng khi và cùng phương với nhau.
C sai vì với 3 vectơ khác đồng phẳng với nhau ta có .
Khi đó
Đặt thì nhưng lại đồng phẳng với nhau.
Vậy cả ba khẳng định trên đều sai.
Câu 24:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Phương án D sai do đẳng thức luôn đúng với vị trí bất kì trong không gian của bốn điểm nên không đủ điều kiện để khẳng định đồng phẳng.
Câu 25:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có:
Câu 26:
 Xem đáp án
Xem đáp án
Chọn đáp án B
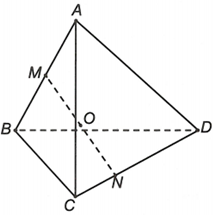
Ta có , trong đó ;
VậyCâu 27:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Gọi G là trọng tâm thì G cố định và
Ta cos:
Dấu “=” xảy ra
Vậy với là trọng tâm tam giác ABC.
Câu 28:
 Xem đáp án
Xem đáp án
Chọn đáp án B
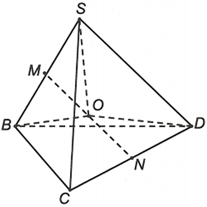
Ta có
Mà
Từ (1) và (2) ta có
Câu 29:
Cho lăng trụ ABC.A'B'C'. Đặt
Xét hai mệnh đề
(I) (II)
Mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án A
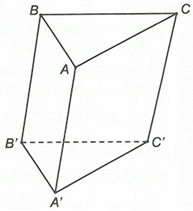
(I) Đúng vì
(II) Sai vì
Câu 30:
 Xem đáp án
Xem đáp án
Chọn đáp án B
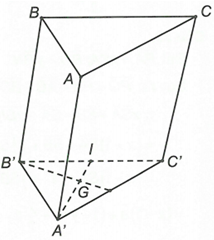
Ta có:
Câu 31:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Đặt
Từ , ta có
Từ , ta có
Suy ra
Mặt khác
Để thì nên
Từ đó ta có: . VậyCâu 32:
 Xem đáp án
Xem đáp án
Chọn đáp án A
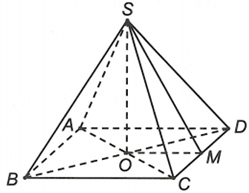
Do tất cả các cạnh của hình chóp bằng nhau nên hình chóp S.ABCD là hình chóp đều.
Suy ra đôi một vuông góc.
Do M là trung điểm của CD nên ta có:
Do đôi một vuông góc với nhau nên
Câu 33:
 Xem đáp án
Xem đáp án
Chọn đáp án D
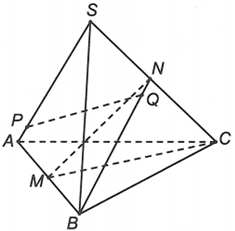
Đặt
Suy ra:
(*)
Lại có
Để thì hay
Thay vào (*) ta được
Câu 34:
 Xem đáp án
Xem đáp án
Chọn đáp án C
C sai vì khi ta vẫn có đồng phẳng nhưng hay giá của không nằm trong .
Câu 35:
 Xem đáp án
Xem đáp án
Chọn đáp án B
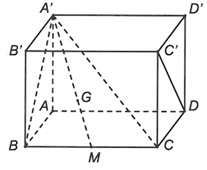
Suy ra
Câu 36:
Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề
(I). Nếu ABCD là hình bình hành thì .
(II). Nếu thì ABCD là hình bình hành.
Mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án D
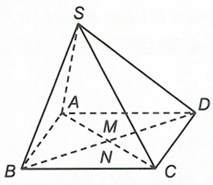
Gọi M, N lần lượt là trung điểm của AC và BD. Do O là giao điểm của AC và BD nên
là hình bình hành.
Vậy mệnh đề (I) và (II) đều đúng.
Bình luận: Để chứng minh mệnh đề (I) và (II) đúng, ta áp dụng: Cho và .
Khi đó .
Chứng minh: Nếu A không trùng O thì B không trùng O (do ) và
Nhưng thẳng hàng (trái với giả thiết )
Câu 37:
 Xem đáp án
Xem đáp án
Chọn đáp án A
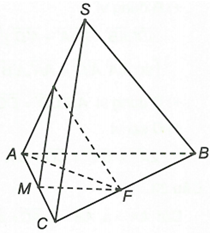
Từ giả thiết suy ra vuông cân tại là tam giác đều.
Có
Vậy
Câu 38:
Cho hình chóp S.ABCD. Xét hai mệnh đề
(I) Nếu ABCD là hình bình hành thì .
(II) Nếu thì ABCD là hình bình hành.
Mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Gọi M, N lần lượt là trung điểm của AC và BD.
Ta có: là hình bình hành.
Câu 39:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có nên ba vectơ đồng phẳng.
Câu 40:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Khẳng định B sai.
Các vectơ đồng phẳng
Ta có
(hệ vô nghiệm).
Vậy không tồn tại hai số
Câu 41:
Trong các kết quả sau đây, kết quả nào đúng?
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Giá trị của bằng
 Xem đáp án
Xem đáp án
Chọn đáp án A
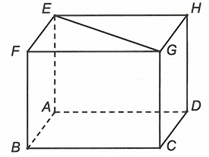
Ta có
Do nên
Suy ra
Câu 42:
 Xem đáp án
Xem đáp án
Chọn đáp án D
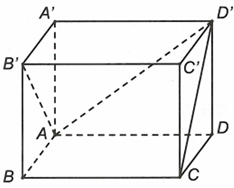
+) A đúng vì
Suy ra
+) B đúng vì
+) C đúng vì
+) D sai vì
Câu 43:
 Xem đáp án
Xem đáp án
Chọn đáp án C
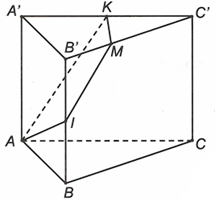
Đặt
Ta có
Do nên
Vì bốn điểm đồng phẳng nên đồng phẳng, do đó
Vậy
Câu 44:
 Xem đáp án
Xem đáp án
Chọn đáp án D
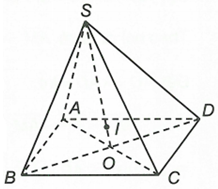
Gọi I là điểm thỏa mãn
Vậy
Câu 45:
 Xem đáp án
Xem đáp án
Chọn đáp án B
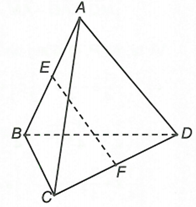
Áp dụng công thức độ dài đường trung tuyến, ta có:
Câu 46:
 Xem đáp án
Xem đáp án
Chọn đáp án D
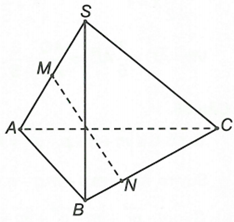
Đặt , ta có:
Để ba vectơ đồng phẳng ta có
Vậy
Câu 47:
 Xem đáp án
Xem đáp án
Chọn đáp án B
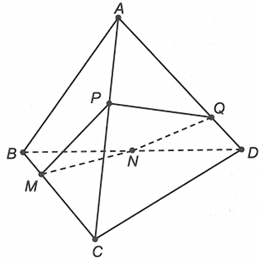
Đặt
Theo bài ra ta có
Đặt
Ta có
Vì đồng phẳng nên
Vậy
Câu 48:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có
Suy ra
Vậy
Dấu “=” xảy ra chẳng hạn khi và .
