Trắc nghiệm Đại cương về mặt phẳng và đường thẳng có đáp án (Nhận biết)
-
2410 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
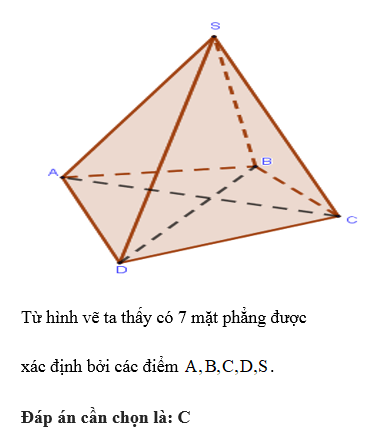
Cho 2 đường thẳng cắt nhau và không đi qua điểm A. Xác định được nhiều nhất bao nhiêu mặt phẳng bởi a, b và A?
Xem đáp án
Có 3 mặt phẳng gồm
.
Đáp án cần chọn là: C
Câu 2:
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Xem đáp án
A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng
thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
B sai. Trong trường hợp điểm thuộc đường thẳng đã cho,
khi đó ta chỉ có 1 đường thẳng, có vô số mặt phẳng
đi qua đường thẳng đó.
D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng
thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong
trường hợp 4 điểm mặt phẳng không đồng phẳng thì
sẽ tạo không tạo được mặt phẳng nào đi qua cả 4 điểm.
Đáp án cần chọn là: C
Câu 3:
Trong các mệnh đề sau mệnh đề nào sai?
Xem đáp án
Hình biểu diễn của hai đường thẳng cắt nhau
là hai đường thẳng cắt nhau, không thể
là hai đường thẳng song song.
Đáp án cần chọn là: D
Câu 4:
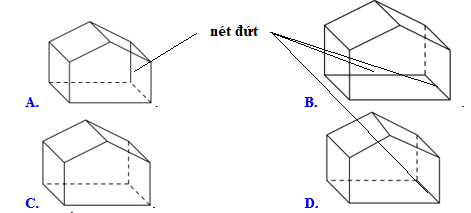
Hình nào sau đây vẽ đúng quy tắc?
Xem đáp án
Quy tắc: phần nhìn thấy vẽ nét liền,
phần không nhìn thấy vẽ nét đứt
Đáp án cần chọn là: A
Câu 5:
Một hình không gian có hình chiếu đứng (nhìn từ trước vào (có thể nhìn từ sau) để từ hình 3D chuyển sang hình 2D) hình chiếu bằng (nhìn từ trên xuống) có thể nhìn từ dưới lên), hình chiếu cạnh (từ trái sang (có thể nhìn từ phải sang) lần lượt được thể hiện như sau:
Xem đáp án
Đáp án A, B, D: Sai vì đoạn thẳng trong
hình phải vẽ nét đứt vì không nhìn thấy.
Đáp án cần chọn là: C
Câu 7:
Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho?
Xem đáp án
Do bốn điểm không đồng phẳng nên không tồn tại
bộ ba điểm thẳng hàng trong số bốn điểm đó. Cứ
ba điểm không thẳng hàng xác định một mặt phẳng
nên số mặt phẳng phân biệt có thể lập được
từ bốn điểm đã cho là .
Đáp án cần chọn là: C
Câu 8:
Trong các khẳng định sau, khẳng định nào đúng?
Xem đáp án
A sai. Qua 2 điểm phân biệt, tạo được 1 đường thẳng,
khi đó chưa đủ điều kiện để lập một mặt phẳng xác định.
Có vô số mặt phẳng đi qua 2 điểm đã cho.
B sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì chỉ tạo được đường thẳng, khi đó có vô số mặt phẳng đi qua 3 điểm phân biệt thẳng hàng.
D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng
thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong
trường hợp 4 điểm mặt phẳng không đồng phẳng
thì sẽ tạo không tạo được mặt phẳng nào đi qua cả 4 điểm.
Đáp án cần chọn là: C
Câu 9:
Trong , cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. Điểm . Có mấy mặt S phẳng tạo bởi và hai trong số bốn điểm nói trên?
Xem đáp án
Điểm cùng với hai trong số bốn điểm
tạo thành một mặt phẳng, từ bốn điểm ta
có 6 cách chọn ra hai điểm, nên có tất cả
6 mặt phẳng tạo bởi và hai trong số bốn điểm nói trên.
Đáp án cần chọn là: C
Câu 10:
Trong mặt phẳng cho tứ giác ABCD, điểm . Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm A, B, C, D, E ?
Xem đáp án
Điểm và 2 điểm bất kì trong 4 điểm
tạo thành 6 mặt phẳng, bốn điểm
tạo thành 1 mặt phẳng.
Vậy có tất cả 7 mặt phẳng.
Đáp án cần chọn là: B
Câu 11:
Cho tứ giác ABCD . Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh của tứ giác ABCD.
Xem đáp án
4 điểm tạo thành 1 tứ giác,
khi đó 4 điểm đã đồng phẳng
và tạo thành 1 mặt phẳng duy
nhất là mặt phẳng .
Đáp án cần chọn là: A
Câu 12:
Cho năm điểm A, B, C, D, E trong đó không có bốn điểm nào ở trên cùng một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?
Xem đáp án
Cứ chọn ra ba điểm trong số năm điểm
ta sẽ có một mặt phẳng. Từ năm điểm ta có
cách chọn ra ba điểm bất kỳ trong số năm
điểm đã cho, nên có 10 mặt phẳng tạo
bởi ba trong số năm điểm đã cho.
Đáp án cần chọn là: A
Câu 13:
Trong các hình sau:
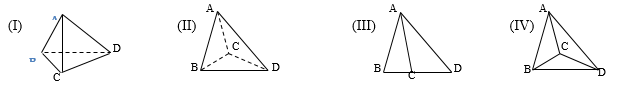
Xem đáp án
Hình (III) không biểu diễn
hình tứ diện vì đó là hình phẳng
Đáp án cần chọn là: C
Câu 15:
Số phần tử của tập hợp các điểm chung của một đường thẳng và một mặt phẳng không thể là:
Xem đáp án
Chỉ có 3 vị trí tương đối của
đường thẳng và mặt phẳng:
Nếu đường thẳng song song với
mặt phẳng thì số điểm chung là giữa chúng là 0
Nếu đường thẳng cắt mặt phẳng
tại 1 điểm duy nhất thì số điểm chúng là 1
Nếu đường thẳng nằm trong mặt phẳng
thì giữa chúng có vô số điểm chung.
Đáp án cần chọn là: C