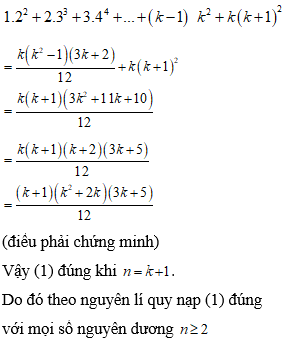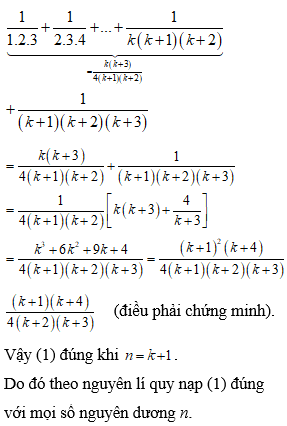21 câu hỏi trắc nghiệm thuộc Dạng 1: Quy nạp toán học có đáp án

Câu 1:

n \geq 2

, ta luôn có

2^{n + 1} > 2 n + 3 (*)

Xem đáp án

Câu 2:

Chứng minh rằng với mọi số nguyên dương n, ta có $1.4 + 2.7 + ... + n (3 n + 1) = n {(n + 1)}^{2} (1)$

Xem đáp án

Câu 3:

Chứng minh rằng với mọi số nguyên dương $n \geq 2$ , ta có ${1.2}^{2} + {2.3}^{3} + {3.4}^{4} + ... + (n - 1) n^{2} = \frac{n (n^{2} - 1) (3 n + 2)}{12} (1)$

Xem đáp án

Câu 4:

Chứng minh rằng với mọi số nguyên dương n, ta có $\frac{1}{1.2.3} + \frac{1}{2.3.4} + ... + \frac{1}{n (n + 1) (n + 2)} = \frac{n (n + 3)}{4 (n + 1) (n + 2)} (1)$

Xem đáp án

Câu 5:

Chứng minh rằng với mọi số nguyên dương $n \geq 2$ ta có $\frac{1}{n + 1} + \frac{1}{n + 2} + ... + \frac{1}{n + n} > \frac{13}{24} (1)$

Xem đáp án

Câu 6:

Chứng minh rằng số đường chéo của một đa giác lồi n cạnh

(n \geq 4)

là

\frac{n (n - 3)}{2} .

Xem đáp án

Câu 7:

Chứng minh rằng mọi n – giác lồi

(n \geq 5)

đều được chia thành hữu hạn ngũ giác lồi.

Xem đáp án

Câu 8:

Với mỗi số nguyên dương n, kí hiệu

u_{n} = 9^{n} - 1.

Chứng minh rằng với mọi số nguyên dương n thì u_n luôn chia hết cho 8.

Xem đáp án

Câu 9:

Chứng minh rằng với mọi

n \in ℕ^{*}, n (n + 1) (n + 2) (n + 3) (n + 4)

chia hết cho 120.

Xem đáp án

Câu 10:

Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên

n \geq p

(p là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề A(n) đúng với n = k. Khẳng định nào sau đây là đúng?

A. k > p

B. $k \geq p$

C. k = p

D. k < p

Xem đáp án

Chọn B

Mệnh đề A(n) đúng với n=k với $k \geq p$

Câu 11:

Với mỗi số nguyên dương, kí hiệu $u_{n} = {5.2}^{3 n - 2} + 3^{3 n - 1}$

Một học sinh chứng minh u_n luôn chia hết cho 19 như sau:

Bước 1: Khi n=1 ta có $u_{1} = {5.2}^{1} + 3^{2} = 19 \Rightarrow u_{1} ⋮ 19$

Bước 2: Giả sử $u_{k} = {5.2}^{3 k - 2} + 3^{3 k + 1}$ chia hết cho 19 với $k \geq 1$

Khi đó ta có $u_{k + 1} = {5.2}^{3 k + 1} + 3^{3 k + 2} = 8 ({5.2}^{3 k - 2} + 3^{3 k - 1}) + {19.3}^{3 k - 1}$

Bước 3: Vì ${5.2}^{3 k - 2} + 3^{3 k - 1} và {19.3}^{3 k - 1}$ chia hết cho 19 nên $u_{k + 1}$ chia hết cho 19,

Vậy u_n chia hết cho 19, $\forall n \in ℕ^{*}$

Lập luận trên đúng hay sai? Nếu sai thì bắt đầu từ bước nào?

A. Sai từ bước 1

B. Sai từ bước 3

C. Sai từ bước 2

D. Lập luận hoàn toàn đúng

Xem đáp án

Chọn D

Lập luận hoàn toàn đúng.

Câu 12:

Với mỗi số nguyên dương, kí hiệu $u_{n} = {5.2}^{3 n - 2} + 3^{3 n - 1}$

Một học sinh chứng minh u_n luôn chia hết cho 19 như sau:

Bước 1: Khi n=1 ta có $u_{1} = {5.2}^{1} + 3^{2} = 19 \Rightarrow u_{1} ⋮ 19$

Bước 2: Giả sử $u_{k} = {5.2}^{3 k - 2} + 3^{3 k + 1}$ chia hết cho 19 với $k \geq 1$

Khi đó ta có $u_{k + 1} = {5.2}^{3 k + 1} + 3^{3 k + 2} = 8 ({5.2}^{3 k - 2} + 3^{3 k - 1}) + {19.3}^{3 k - 1}$

Bước 3: Vì ${5.2}^{3 k - 2} + 3^{3 k - 1} và {19.3}^{3 k - 1}$ chia hết cho 19 nên $u_{k + 1}$ chia hết cho 19,

Vậy u_n chia hết cho 19, $\forall n \in ℕ^{*}$

Lập luận trên đúng hay sai? Nếu sai thì bắt đầu từ bước nào?

A. Sai từ bước 1

B. Sai từ bước 3

C. Sai từ bước 2

D. Lập luận hoàn toàn đúng

Xem đáp án

Chọn D

Lập luận hoàn toàn đúng.

Câu 13:

Với mỗi số nguyên dương, kí hiệu $u_{n} = {5.2}^{3 n - 2} + 3^{3 n - 1}$

Một học sinh chứng minh u_n luôn chia hết cho 19 như sau:

Bước 1: Khi n=1 ta có $u_{1} = {5.2}^{1} + 3^{2} = 19 \Rightarrow u_{1} ⋮ 19$

Bước 2: Giả sử $u_{k} = {5.2}^{3 k - 2} + 3^{3 k + 1}$ chia hết cho 19 với $k \geq 1$

Khi đó ta có $u_{k + 1} = {5.2}^{3 k + 1} + 3^{3 k + 2} = 8 ({5.2}^{3 k - 2} + 3^{3 k - 1}) + {19.3}^{3 k - 1}$

Bước 3: Vì ${5.2}^{3 k - 2} + 3^{3 k - 1} và {19.3}^{3 k - 1}$ chia hết cho 19 nên $u_{k + 1}$ chia hết cho 19,

Vậy u_n chia hết cho 19, $\forall n \in ℕ^{*}$

Lập luận trên đúng hay sai? Nếu sai thì bắt đầu từ bước nào?

A. Sai từ bước 1

B. Sai từ bước 3

C. Sai từ bước 2

D. Lập luận hoàn toàn đúng

Xem đáp án

Chọn D

Lập luận hoàn toàn đúng.

Câu 14:

Giả sử A là tập con của tập hợp các số nguyên dương sao cho:

$(I) k \in A; (I I) n \in A \Rightarrow n + 1 \in A, \forall n \geq k$

Lúc đó ta có

A. Mọi số nguyên bé hơn k đều thuộc A.

B. Mọi số nguyên dương đều thuộc A.

C. Mọi số nguyên dương lớn hơn hoặc bằng k đều thuộc A.

D. Mọi số nguyên đều thuộc A.

Xem đáp án

Chọn C

$(I) k \in A :$ số nguyên dương k thuộc tập A.

(I I) n \in A \Rightarrow n + 1 \in A, \forall n \geq k :

nếu số nguyên dương

n (n \geq k)

thuộc tập A thì số nguyên dương đứng ngay sau nó (n+1) cũng thuộc A. Mọi số nguyên dương lớn hơn hoặc bằng k đều thuộc A.

Câu 15:

Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến A(n) đúng với mọi giá trị nguyên $n \geq p$ với p là số nguyên dương ta sẽ tiến hành 2 bước

Bước 1 (bước cơ sở). Chứng minh rằng A(n) đúng khi n=1

Bước 2 (bước quy nạp). Với số nguyên dương tùy ý k, ta giả sử A(n) đúng khi n=k (theo giả thiết quy nạp). Ta sẽ chứng minh rằng A(n) đúng khi n=k+1

Hãy chọn câu trả lời đúng tương ứng với lí luận trên.

A. Chỉ có bước 2 đúng.

B. Cả hai bước đều đúng.

C. Cả hai bước đều sai.

D. Chỉ có bước 1 đúng.

Xem đáp án

Chọn C

Bước 1 sai, vì theo bài toán $n \geq p$ nên ta phải chứng minh rằng A(n) đúng khi n=p.

Bước 2 sai, không thể “Với số nguyên dương tùy ý k” mà phải là “Với số nguyên dương $k \geq p$ ”.

Câu 16:

Với mọi

n \in ℕ^{*},

khẳng định nào sau đây sai?

A. $1 + 2 + ... + n = \frac{n (n + 1)}{2} .$

B. $1 + 3 + 5 + ... + (2 n - 1) = n^{2} .$

C. $1^{2} + 2^{2} + ... + n^{2} = \frac{n (n + 1) (n + 2)}{6} .$

D. $2^{2} + 4^{2} + 6^{2} + ... + {(2 n)}^{2} = \frac{2 n (n + 1) (2 n + 1)}{6} .$

Xem đáp án

Chọn D

Thử với n=1, n=2, n=3 ta kết luận được đáp án D sai.

Ta có $2^{2} + 4^{2} + 6^{2} + ... + {(2 n)}^{2} = \frac{2 n (n + 1) (2 n + 1)}{3}$ mới là kết quả đúng.

Câu 17:

Cho

S_{n} = \frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} + ... + \frac{1}{n (n + 1)} với n \in ℕ *

. Mệnh đề nào sau đây đúng?

A. $S_{n} = \frac{n - 1}{n} .$

B. $S_{n} = \frac{n}{n + 1} .$

C. $S_{n} = \frac{n + 1}{n + 2} .$

D. $S_{n} = \frac{n + 2}{n + 3} .$

Xem đáp án

Chọn B

Ta có $S_{1} = \frac{1}{2}, S_{2} = \frac{2}{3}, S_{3} = \frac{3}{4} \Rightarrow$ dự đoán $S_{n} = \frac{n}{n + 1}$

Với n=1 ta được $S_{1} = \frac{1}{1.2} = \frac{1}{1 + 1}$ (đúng)

Giả sử mệnh đề đúng khi $n = k (k \geq 1) t ứ c l à \frac{1}{1.2} + \frac{1}{2.3} + ... + \frac{1}{k (k + 1)} = \frac{k}{k + 1}$

Ta có:

$\frac{1}{1.2} + \frac{1}{2.3} + ... + \frac{1}{k (k + 1)} = \frac{k}{k + 1} \begin{array}{l} \Leftrightarrow \frac{1}{1.2} + \frac{1}{2.3} + ... + \frac{1}{k (k + 1)} + \frac{1}{(k + 1) (k + 2)} = \frac{k}{k + 1} + \frac{1}{(k + 1) (k + 2)} \\ \Leftrightarrow \frac{1}{1.2} + \frac{1}{2.3} + ... + \frac{1}{k (k + 1)} + \frac{1}{(k + 1) (k + 2)} = \frac{k^{2} + 2 k + 1}{(k + 1) (k + 2)} \\ \Leftrightarrow \frac{1}{1.2} + \frac{1}{2.3} + ... + \frac{1}{k (k + 1)} + \frac{1}{(k + 1) (k + 2)} = \frac{k + 1}{k + 2} \end{array}$

Suy ra mệnh đề đúng với n=k+1

Câu 18:

Cho dãy số (u_n) với $\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} + {(- 1)}^{2 n} \end{cases} .$ Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. $u_{n} = 1 + n .$

B. $u_{n} = 1 - n .$

C. $u_{n} = 1 + {(- 1)}^{2 n} .$

D. $u_{n} = n .$

Xem đáp án

Chọn D

Ta có $u_{n + 1} = u_{n} + {(- 1)}^{2 n} = u_{n} + 1 \Rightarrow u_{2} = 2; u_{3} = 3; u_{4} = 4; ...$

Dễ dàng dự đoán được $u_{n} = n$

Thật vậy, ta chứng minh được $u_{n} = n (*)$ bằng phương pháp quy nạp như sau

Với $n = 1 \Rightarrow u_{1} = 1$ . Vậy (*) đúng với n=1.

Giả sử (*) đúng với $n = k (k \in ℕ^{*})$ , ta có $u_{k} = k$

Ta đi chứng minh (*) cũng đúng với n=k+1, tức là $u_{k + 1} = k + 1$

Thật vậy, từ hệ thức xác định dãy số $(u_{n})$ ta có $u_{k + 1} = u_{k} + {(- 1)}^{2 k} = k + 1$

Vậy (*) đúng với mọi $n \in ℕ *$ . Số hạng tổng quát của dãy số là $u_{n} = n$

Câu 19:

Cho dãy xác định bởi công thức

\{\begin{cases} u_{1} = 3 \\ u_{n + 1} = \frac{1}{2} u_{n}, \forall n \in ℕ^{*} \end{cases} .

Số hạng tổng quát của dãy u_n là

A. $u_{n} = \frac{3}{2^{n - 1}} .$

B. $u_{n} = \frac{3}{2^{n}} .$

C. $u_{n} = \frac{3}{2^{n} + 1} .$

D. $u_{n} = \frac{3}{2^{n} - 1} .$

Xem đáp án

Chọn A

Ta có $u_{1} = 3; u_{2} = \frac{1}{2} u_{1} = \frac{3}{2}; u_{3} = \frac{1}{2} u_{2} = \frac{3}{2^{2}}; ...$

Ta đi chứng minh cho dãy số có số hạng tổng quát là $u_{n} = \frac{3}{2^{n - 1}}$

Thật vậy, n=1 thì $u_{1} = 3$ (đúng).

Giả sử với $n = k (k \geq 1)$ thì $u_{k} = \frac{3}{2^{k - 1}}$ . Ta đi chứng minh $u_{k + 1} = \frac{3}{2^{k}}$

Ta có $u_{k + 1} = \frac{1}{2} u_{k} = \frac{1}{2} . \frac{3}{2^{k - 1}} = \frac{3}{2^{k}}$ (điều phải chứng minh).

Vậy số hạng tổng quát của dãy số là $u_{n} = \frac{3}{2^{n - 1}}$

Câu 20:

Cho hai dãy số $(u_{n}), (v_{n})$ được xác định như sau $u_{1} = 3, v_{1} = 2 và \{\begin{cases} u_{n + 1} = u_{n}^{2} + 2 v_{n}^{2} \\ v_{n = 1} = 2 u_{n} . v_{n} \end{cases}$ với $n \geq 2 .$ Công thức tổng quát của hai dãy $(u_{n}) v à (v_{n})$ là

A. $\{\begin{cases} u_{n} = {(\sqrt{2} + 1)}^{2 n} + {(\sqrt{2} - 1)}^{2 n} \\ v_{n} = \frac{1}{2 \sqrt{2}} [{(\sqrt{2} + 1)}^{2 n} - {(\sqrt{2} - 1)}^{2 n}] \end{cases} .$

B. $\{\begin{cases} u_{n} = \frac{1}{2} [{(\sqrt{2} + 1)}^{2 n} + {(\sqrt{2} - 1)}^{2 n}] \\ v_{n} = \frac{1}{2 \sqrt{2}} [{(\sqrt{2} + 1)}^{2 n} - {(\sqrt{2} - 1)}^{2 n}] \end{cases} .$

C. $\{\begin{cases} u_{n} = \frac{1}{2} [{(\sqrt{2} + 1)}^{2 n} + {(\sqrt{2} - 1)}^{2 n}] \\ v_{n} = \frac{1}{3 \sqrt{2}} [{(\sqrt{2} + 1)}^{2 n} - {(\sqrt{2} - 1)}^{2 n}] \end{cases} .$

D. $\{\begin{cases} u_{n} = \frac{1}{4} [{(\sqrt{2} + 1)}^{2 n} + {(\sqrt{2} - 1)}^{2 n}] \\ v_{n} = \frac{1}{2} [{(\sqrt{2} + 1)}^{2 n} - {(\sqrt{2} - 1)}^{2 n}] \end{cases} .$

Xem đáp án

Chọn B

Chứng minh $u_{n} - \sqrt{2} v_{n} = {(\sqrt{2} - 1)}^{2 n} (1)$

Ta có $u_{n} = \sqrt{2} v_{n} = u_{n - 1}^{2} + 2 v_{n - 1}^{2} - 2 \sqrt{2} u_{n - 1} v_{n - 1} = {(u_{n - 1} - \sqrt{2} v_{n - 1})}^{2}$

Mặt khác $u_{1} - \sqrt{2} v_{1} = 3 - 2 \sqrt{2} = {(\sqrt{2} - 1)}^{2}$ nên (1) đúng với n=1

Giả sử $u_{k} - \sqrt{2} v_{k} = {(\sqrt{2} - 1)}^{2 k}$ , ta có $u_{k - 1} - \sqrt{2} v_{k + 1} = {(u - \sqrt{2} v_{k})}^{2} = {(\sqrt{2} - 1)}^{2 k + 1}$

Vậy (1) đúng với $\forall n \geq 1$

Ta có $u_{n} + \sqrt{2} v_{n} = {(\sqrt{2} + 1)}^{2^{n}}$

Do đó ta suy ra

\{\begin{cases} 2 u_{n} = {(\sqrt{2} + 1)}^{2^{n}} + {(\sqrt{2} - 1)}^{2^{n}} \\ 2 \sqrt{2} v_{n} = {(\sqrt{2} + 1)}^{2^{n}} - {(\sqrt{2} - 1)}^{2^{n}} \end{cases} \Rightarrow \{\begin{cases} u_{n} = \frac{1}{2} [{(\sqrt{2} + 1)}^{2^{n}} + {(\sqrt{2} - 1)}^{2^{n}}] \\ v_{n} = \frac{1}{2 \sqrt{2}} [{(\sqrt{2} + 1)}^{2^{n}} - {(\sqrt{2} - 1)}^{2^{n}}] \end{cases}

Câu 21:

Cho dãy số

(u_{n})

xác định bởi

\{\begin{cases} u_{1} = \cos α (0 < α < π) \\ u_{n + 1} = \sqrt{\frac{1 + u_{n}}{2}}, \forall n \geq 1 \end{cases}

. Số hạng thứ 2020 của dãy số đã cho là

A. $u_{2020} = \cos (\frac{α}{2^{2020}}) .$

B. $u_{2020} = \cos (\frac{α}{2^{2019}}) .$

C. $u_{2020} = \sin (\frac{α}{2^{2021}}) .$

D. $u_{2020} = \sin (\frac{α}{2^{2020}}) .$

Xem đáp án

Chọn B

Do $0 < α < π$ nên $u_{2} = \sqrt{\frac{1 + \cos α}{2}} = \sqrt{\cos^{2} \frac{α}{2}} = \cos \frac{α}{2}; u_{3} = \sqrt{\frac{1 + \cos \frac{α}{2}}{2}} = \sqrt{\cos^{2} \frac{α}{2}} = \cos \frac{α}{4}$

Vậy $u = \cos (\frac{α}{2^{n - 1}})$ với mọi $n \in ℕ *$ . Ta sẽ chứng minh bằng quy nạp.

Với n=1 thì $u_{1} = \cos α$ (đúng).

Giả sử với $n = k \in ℕ^{*}$ ta có $u_{k} = \cos (\frac{α}{2^{k - 1}})$ . Ta chứng minh $u_{k + 1} = \cos (\frac{α}{2^{k - 1}})$

Thật vậy $u_{k + 1} = \sqrt{\frac{1 + u_{k}}{2}} = \sqrt{\frac{1 + \cos (\frac{α}{2^{k - 1}})}{2}} = \sqrt{\cos^{2} (\frac{α}{2^{k}})} = \cos (\frac{α}{2^{k}})$

Từ đó ta có

u_{2020} = \cos (\frac{α}{2^{2019}})

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập chuyên đề Toán 11 Bài 1: Phương pháp quy nạp toán học. Dãy số có đáp án

Dạng 1: Quy nạp toán học có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương