Dạng 1. Dùng định nghĩa tính đạo hàm
-
1141 lượt thi
-
32 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Dùng định nghĩa tính đạo hàm của hàm số tại .
 Xem đáp án
Xem đáp án
Giả sử là số gia của đối số tại .
Ta có:
Tỉ số .
Vậy
Câu 2:
Dùng định nghĩa tính đạo hàm của hàm số tại .
 Xem đáp án
Xem đáp án
Giả sử là số gia của đối số tại .
Ta có:
Do đó
Vậy
Câu 3:
Dùng định nghĩa tính đạo hàm của hàm số tại
 Xem đáp án
Xem đáp án
Giả sử là số gia của đối số tại
Ta có:
.
Vậy
Câu 4:
Dùng định nghĩa tính đạo hàm của hàm số tại
 Xem đáp án
Xem đáp án
Giả sử là số gia của đối số
Ta có:
Do đó
Vì nên .
Vậy
Câu 5:
Chứng minh rằng hàm số không có đạo hàm tại nhưng có đạo
hàm tại .
 Xem đáp án
Xem đáp án
Ta có
Suy ra hàm số gián đoạn tại nên không có đạo hàm tại đó.
Vậy hàm số có đạo hàm tại và
Câu 6:
Chứng minh rằng hàm số liên tục tại nhưng không có đạo hàm tại điểm đó.
 Xem đáp án
Xem đáp án
Vì là hàm số sơ cấp xác định tại nên nó liên tục tại đó.
Ta có:
Do đó nên không có đạo hàm tại .
Câu 7:
Cho đồ thị hàm số xác định trên khoảng như hình vẽ.
Dựa vào hình vẽ hãy cho biết tại mỗi điểm
a, Hàm số có liên tục không?
b, Hàm số có đạo hàm không?
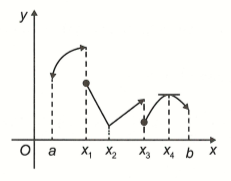
 Xem đáp án
Xem đáp án
a, Hàm số gián đoạn tại các điểm vì đồ thị bị đứt tại các điểm đó. Hàm số liên tục tại vì đồ thị là đường liền nét khi đi qua các điểm đó.
b, Tại các điểm hàm số không có đạo hàm do hàm số gián đoạn tại các điểm
Hàm số không có đạo hàm tại vì đồ thị bị gãy (không có tiếp tuyến tại đó).
Hàm số có đạo hàm tại và vì tại đồ thị hàm số có tiếp tuyến và tiếp tuyến song song với trục hoành (hệ số góc của tiếp tuyến bằng 0).
Câu 8:
Dùng định nghĩa tính đạo hàm của hàm số trên khoảng ?
 Xem đáp án
Xem đáp án
Giả sử là số gia của đối số .
Ta có:
Tỉ số
Vậy
Câu 9:
Dùng định nghĩa tính đạo hàm của hàm số trên các khoảng và ?
 Xem đáp án
Xem đáp án
Giả sử là số gia của đối số x .
Ta có
.
Vậy .
Câu 11:
Tìm để hàm số có đạo hàm tại .
 Xem đáp án
Xem đáp án
Ta có
Để hàm số có đạo hàm tại thì phải liên tục tại , suy ra
Thay vào hàm số thỏa mãn có đạo hàm .Câu 12:
Tìm a, b để hàm số có đạo hàm tại
 Xem đáp án
Xem đáp án
Để hàm số có đạo hàm tại thì hàm số liên tục tại .
Do đó . Ta lại có:
Do nên
Để hàm số có đạo hàm tại thì
Câu 13:
Chứng minh rằng hàm số không có đạo hàm tại .
 Xem đáp án
Xem đáp án
Ta có:
.
Suy ra hàm số gián đoạn tại nên không có đạo hàm tại đó.
Câu 14:
Tìm để hàm số có đạo hàm tại .
 Xem đáp án
Xem đáp án
Điều kiện cần
Ta có và
Để hàm số có đạo hàm tại thì liên tục tại .
Do đó
Điều kiện đủ:
Để hàm số có đạo hàm tại thì
Vậy thỏa mãn yêu cầu của bài toánCâu 18:
Đạo hàm của hàm số tại điểm là
 Xem đáp án
Xem đáp án
Đáp án D
Xét hàm số . Gọi là số gia của đối số tại x .
Ta có
Suy ra .
Vậy
Câu 24:
Đạo hàm của hàm số tại bằng
 Xem đáp án
Xem đáp án
Đáp án A
Ta có nên hàm số liên tục tại .
Ta lại có: và
Vậy
Câu 25:
Cho hàm số . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Hàm số có tập xác định là .
Ta có nên hàm số liên tục tại .
Ta có nên
và
Vậy không tồn tại . Do đó hàm số không có đạo hàm tại .
Câu 26:
Đạo hàm của hàm số tại bằng
 Xem đáp án
Xem đáp án
Đáp án D
Ta có
Suy ra hàm số không liên tục tại nên hàm số không có đạo hàm tại .
Câu 30:
Giá trị của m để hàm số có đạo hàm tại bằng
 Xem đáp án
Xem đáp án
Đáp án B
Ta dễ dàng chứng minh được
Để hàm số liên tục tại thì
Mặt khác
Vậy với thì hàm số dã cho có đạo hàm tại .
Câu 31:
Cho hàm số biết hàm số có đạo hàm tại điểm .
Giá trị của ab bằng
 Xem đáp án
Xem đáp án
Đáp án D
Để hàm số có đạo hàm tại thi hàm số phải liên tục tại .
Do đó
Hàm số có đạo hàm tại điểm nên
Suy ra . Vậy
Câu 32:
Nếu hàm số có đạo hàm trên R thì giá trị là
 Xem đáp án
Xem đáp án
Đáp án B
Với hàm số luôn có đạo hàm nên để hàm số có đạo hàm với mọi thì hàm số phải có đạo hàm tại .
Ta có: . Để hàm số liên tục tại thì
Với , ta có:
Hàm số có đạo hàm tại điểm khi và chỉ khi:
Vậy
