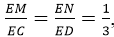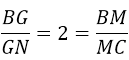24 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 3: Đường thẳng và mặt phẳng song song (phần 1) (có đáp án)

Câu 1:

Với điều kiện nào sau đây thì đường thẳng a song song với mặt phẳng (∝) ?

A. a // b và b ∩ (∝) = ∅

B. a // b và b // (∝)

C. a // b và b ⊂ (∝)

D. a ∩ (∝) = ∅

Xem đáp án

Các phương án A, B, C sai vì a có thể thuộc (∝). Phương án D đúng vì theo định nghĩa.

Đáp án D.

Câu 2:

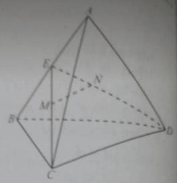
Cho tứ diện ABCD, M, N lần lượt là trọng tâm của tam giác ABC, ABD. Những khẳng định nào sau đây là đúng?

(1) MN //(BCD)

(2) MN //(ACD)

(3) MN // (ABD)

A. Chỉ có (1) đúng

B. (2) và (3)

C. (1) và (2)

D. (1) và (3)

Xem đáp án

Gọi E là trung điểm của AB, M, N lần lượt là trọng tâm của các tam giác ABC, ABD nên:

Theo định lí Ta – lét ta có: MN // CD. (1)

Mà $C D \subset (B C D); C D \subset (A C D)$ (2)

Từ (1) và (2) suy ra: MN // (BCD), MN // (ACD).

Đáp án C.

Câu 3:

Cho tứ diện ABCD, điểm M thuộc AC. Mặt phẳng (∝) đi qua M, song song với AB và AD. Thiết diện (∝) với tứ diện ABCD là hình gì?

A. Thiết diện là tam giác

B. Hình bình hành

C. Hình thoi

D. Hình thang

Xem đáp án

(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB cắt BC tại P.

(∝) // AD nên giao tuyến của (∝) với (ADC) là đường thẳng qua M, song song với AD, cắt DC tại N.

Vậy thiết diện là tam giác MNP.

Đáp án A

Câu 4:

Cho tứ diện ABCD. Giả sử M thuộc đoạn BC. Một mặt (∝) qua M song song với AB và CD. Thiết diện của (∝) và hình tứ diện ABCD là hình gì?

A. Hình thang có đúng một cặp cạnh song song

B. Hình bình hành

C. Hình tam giác

D. Hình ngũ giác

Xem đáp án

(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng đi qua M, song song với AB và cắt AC tại Q.

(∝) // CD nên giao tuyến của (∝) với (BCD) là đường thẳng đi qua M, song song với CD và cắt BD tại N.

(∝) // AB nên giao tuyến của (∝) với (ABD) là đường thẳng đi qua N, song song với AB và cắt AD tại P.

Suy ra, thiết diện của hình chóp cắt bởi ( $α$ ) là tứ giác MNPQ.

* Lại có: MN // PQ // CD, MQ // PN // AB.

Vậy thiết diện là hình bình hành MNPQ.

Đáp án B.

Câu 5:

Có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án C

Có 3 vị trí tương đối giữa đường thẳng và mặt phẳng là:

song song, cắt nhau và đường thẳng nằm trên mặt phẳng

Câu 6:

Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?

A. 1

B. 2

C. không

D. vô số

Xem đáp án

Đáp án A

Câu 7:

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?

A. AC

B. BD

C. AD

D. SC

Xem đáp án

Đáp án C

Vì ABCD là hình bình hành nên AD // BC

* Vì hai mặt phẳng (SAD) và (SBC) lần lượt chứa hai đường thẳng song song là AD và BC, có điểm S chung

Nên giao tuyến của hai mặt phẳng này là đường thẳng đi qua điểm chung S và song song với AD; BC

Chọn đáp án C

Câu 8:

Cho hình chóp S.ABCD, M, N, P, Q lần lượt là trọng tâm các tam giác SAB, SBC, SCD, SDA. Khẳng định nào sau đây là đúng?

A. MNPQ là hình bình hành.

B. MNPQ là hình thoi.

C. MNPQ là hình thang chỉ có một cặp cạnh đối song song.

D. MNPQ là tứ giác không có cặp cạnh nào song song.

Xem đáp án

Đáp án A

Gọi F, G, H, I lần lượt là trung điểm của AB; BC; CD và DA

Vì M, N, P, Q lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.

Do đó ta có: $\frac{S M}{S F} = \frac{S N}{S G} = \frac{S P}{S H} = \frac{S Q}{S I} (= \frac{2}{3})$

Khi đó: MN // FG; NP // GH; QP // IH; MQ // FI

Xét tam giác ABD có FI là đường trung bình (vì F và I lần lượt là trung điểm của AB và AD)

Suy ra FI // BD

Chứng minh tương tự ta có: GH // BD

Nên FI // GH // BD

Tương tự FG // IH // AC

Do đó MQ // NP // FI // GH và MN // PQ // FG // IH

Vậy tứ giác MNPQ là hình bình hành.

Chọn đáp án A

Câu 9:

Cho tứ diện đều ABCD cạnh a. I, J lần lượt là trung điểm của AC và BC. Gọi K là giao điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?

A. thiết diện là hình thang cân.

B. hình bình hành.

C. tam giác.

D. tứ giác không có cặp cạnh nào song song.

Xem đáp án

* Vì I, J lần lượt là trung điểm của AC và BC nên IJ là đường trung bình của tam giác ABC

Suy ra: IJ // AB.

*Tìm giao tuyến của 2 mp( IJK) và mp ( ABD)

2 mặt phẳng này chứa 2 đường thẳng song song là IJ; AB và có điểm K chung

Do đó giao tuyến của (IJK) với (ABD) là đường thẳng đi qua K và song song với AB cắt AD tại H.

Vậy IJ // KH // AB.

Ta có ∆BJK = ∆AIH ⇒ JK = IH. Hơn nữa KH ≠ IJ.

Vậy thiết diện là hình thang cân IJKH

Đáp án A

Câu 10:

Cho hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sẽ:

A. song song với hai đường thẳng đó

B. song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

C. trùng với một trong hai đường thẳng đó

D. cắt một trong hai đường thẳng đó

Xem đáp án

Đáp án B

Câu 11:

Cho tứ diện ABCD. Gọi I; J lần lượt là trung điểm của BC và BD. Giao tuyến của hai mặt phẳng (AIJ) và (ACD) là đường nào sau đây?

A. đường thẳng d đi qua A và d // BC.

B. đường thẳng d đi qua A và d // BD.

C. đường thẳng d đi qua A và d // CD.

D. đường thẳng d đi qua A, M trong đó M là giao điểm IJ và CD.

Xem đáp án

Đáp án C

Tam giác BCD có I và J lần lượt là trung điểm của BC và BD

Nên IJ là đường trung bình của tam giác BCD

Suy ra IJ // BD

Hai mặt phẳng (AIJ) và (ACD) lần lượt chứa hai đường thẳng IJ và CD song song với nhau và có điểm A chung

Nên giao tuyến của hai mặt phẳng này là đường thẳng d đi qua điểm chung A và song song với CD.

Câu 12:

Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm của các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Trong các mệnh đề sau, mệnh đề nào đúng?

A. IJ // (SBD)

B. IJ // (SEF)

C. IJ // (SAB)

D. IJ // (SAD)

Xem đáp án

Đáp án A

Tam giác SAB có I là trọng tâm và E là trung điểm của AB

Nên ta có $\frac{S I}{S E} = \frac{2}{3}$ (1)

Tam giác SAD có J là trọng tâm và F là trung điểm của AD

Nên ta có $\frac{S J}{S F} = \frac{2}{3}$ (2)

Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)

Tam giác ABD có EF là đường trung bình nên EF // BD (4)

Từ (3) và (4) suy ra IJ // BD

Mà BD $\subset$ (SBD)

Do đó IJ // (SBD).

Câu 13:

Cho hình chóp S.ABCD đấy ABCD là hình bình hành tâm O. gọi M, N lần lượt là trung điểm của SA và SB. Giao tuyến của hai mặt phẳng (MNC) và (ABD) là đường nào trong các đường thẳng sau đây?

A. OA

B. OM

C. OC

D. CD

Xem đáp án

Đáp án D

Xét tam giác SAB có M và N lần lượt là trung điểm của SA và SB

Nên MN là đường trung bình của tam giác SAB

MN // AB

Mà AB // CD (ABCD là hình bình hành)

Nên MN // CD

Mặt phẳng (MNC) và (ABD) (hay (ABCD)) lần lượt chứa hai đường thẳng MN và CD song song với nhau

và điểm C chung

nên giao tuyến của hai mặt phẳng này là đường thẳng đi qua điểm chung C và song song với AB,

chính là đường thẳng CD

Câu 14:

Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O. gọi M, N lần lượt là trung điểm của SA và SB. Giao tuyến của hai mặt phẳng (MNO) và (ABCD) là đường nào trong các đường thẳng sau đây?

A. OA

B. OM

C. ON

D. đường thẳng d qua O và d // AB

Xem đáp án

Đáp án D

Theo câu 13, ta có MN // AB

Lại có: O $\in$ (MNO) $\cap$ (ABCD)

Vậy giao tuyến của hai mặt phẳng (MNO) và (ABCD) là đường thẳng d đi qua O và song song với AB.

Câu 15:

Cho đường thẳng d song song với mặt phẳng (∝), mặt phẳng (β) chứa d và cắt (∝) theo giao tuyến d’. Khẳng định nào sau đây là đúng ?

A. d’ // d hoặc d’ ≡ d

B. d’ // d

C. d’ ≡ d

D. d’ và d chéo nhau

Xem đáp án

Đáp án B

Câu 16:

Cho hai đường thẳng a, b và mặt phẳng (∝). Giả sử a // b và b // (∝). Kết luận về vị trí tương đối của a và (∝) nào sau đây là đúng?

A. a // (∝)

B. a ⊂ (∝)

C. a // (∝) hoặc a ⊂ (∝)

D. không xác định

Xem đáp án

Đáp án C

Câu 17:

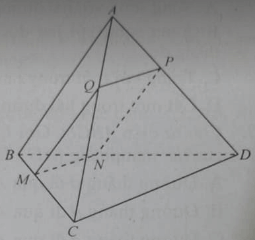
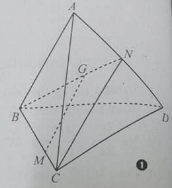
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?

A. MG // (ACD)

B. MG // (ABC)

C. MG // AB

D. MG cắt AC

Xem đáp án

Gọi N là trung điểm của AD

G là trọng tâm của tam giác ABD nên:

⇒ MG // CN.

Do CN thuộc (ACD) nên MG // (ACD).

Đáp án A

Câu 18:

Cho tứ diện ABCD, các điểm E, F, G, H lần lượt thuộc các cạnh AD, AB, BC, CD sao cho

$\frac{E A}{E D} = \frac{F A}{F B} = \frac{G C}{G B} = \frac{H C}{H D}$

Khẳng định nào sau đây là đúng?

A. EFGH là hình bình hành.

B. EFGH có đúng một cặp cạnh song song.

C. EFGH là tứ giác không có cặt cạnh nào song song.

D. EFGH là hình chữ nhật.

Xem đáp án

* Xét tam giác ABD có $\frac{E A}{E D} = \frac{F A}{F B}$ nên EF// BD (1)

*Xét tam giác BCD có $\frac{G C}{G B} = \frac{H C}{H D}$ nên GH// BD (2)

Từ (1) và (2) suy ra: EF// GH// BD

* Chứng minh tương tự ta có: FG // EH // AC

Vậy EFGH là hình bình hành

Đáp án A

Câu 19:

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì?

A. tam giác

B. hình bình hành

C. hình thang

D. hình thoi

Xem đáp án

* Tìm giao tuyến của 2 mp (MCD) và (SAB)

CD// AB; CD ⊂ (MCD); AB ⊂ (SAB)

Điểm M chung

Suy ra: giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB.

Vậy MN // CD. Hơn nữa MN ≠ CD ( vì $M N = \frac{1}{2} A B; A B = C D)$

Vậy thiết diện là hình thang CNMD.

Đáp án C

Câu 20:

Cho hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng, có tâm lần lượt là O và O’. Chọn khẳng định đúng trong các khẳng định sau:

A. OO’ // (ABCD)

B. OO’ // (ABEF)

C. OO’ // (BDF)

D. OO’ / /(ADF)

Xem đáp án

Đáp án D

Ta có: O là trung điểm của BD (hình bình hành ABCD tâm O)

$\Rightarrow \frac{B O}{B D} = \frac{1}{2}$ (1)

Lại có: O’ là trung điểm của BF (hình bình hành ABEF tâm O’)

$\Rightarrow \frac{B O^{'}}{B F} = \frac{1}{2}$ (2)

Từ (1) và (2) suy ra $\frac{B O}{B D} = \frac{B O^{'}}{B F}$

Theo định lý Ta-lét trong tam giác BDF suy ra OO’ // DF

Mà DF $\subset$ (ADF)

Do đó OO’ // (ADF).

Câu 21:

Cho tứ diện ABCD. Hai điểm M, N lần lượt là trung điểm của AC, AD. Mặt phẳng (∝) chứa MN và song song với AB. Thiết diện của (∝) với tứ diện ABCD là:

A. hình thang

B. hình bình hành

C. hình chữ nhật

D. hình vuông

Xem đáp án

Đáp án B

Mặt phẳng $α$ chứa MN song song với AB

Gọi E và F lần lượt là trung điểm của BC và BD

Tam giác ABC có EM là đường trung bình nên ME // = 1/2 AB

Tam giác ABD có FN là đường trung bình nên FN // = 1/2 AB

Suy ra ME // FN // AB và ME = FN

Hay mặt phẳng (MNFE) chính là mặt phẳng $α$

Vậy thiết diện của mặt phẳng $α$ với tứ diện là hình bình hành MNFE (do ME // = FN)

Câu 22:

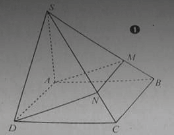
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi O là trung điểm AC. I là 1 điểm bất kì nằm trên BO. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD tại M, N, E, F, J. Khi đó ta có.

A. MN // (SCD)

B. EF // (SAD)

C. NF // (SAD)

D. IJ // (SAB)

Xem đáp án

Đáp án D

* Trong mặt phẳng (ABCD), từ I dựng đường thẳng song song với AC. Cắt AB; BC lần lượt tại N và F.

* trong mp (SAB), từ N dựng đường thẳng song song SB. Cắt SA tại M..

* Trong mp (SBC), từ E dựng đường thẳng song song với SB, cắt SC tại F.

* Trong mp(SBD), từ I dựng đường thẳng song song với SB , cắt SD tại J.

Khi đó mp (P) chính là mp (MNEFJ)

* Theo cách dựng: IJ// SB ; mà SB nằm trong mp(SAB)

suy ra: IJ.// mp(SAB).

Câu 23:

Cho tứ diện ABCD. M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Thiết diện của tứ diện với mặt phẳng (∝) chứa MN và song song với AB là hình gì?

A. tam giác

B. hình bình hành

C. hình thoi

D. hình thang có đúng một cặp cạnh song song

Xem đáp án

(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB, cắt BC tại Q, cắt AC tại G

(∝) // AB nên giao tuyến của (∝) với (ABD) là đường thẳng qua N, song song với AB, cắt BD tại P, cắt AD tại F

Vì 3 mp( BCD); mp(ACD) và mp (PQGF) lần lượt cắt nhau theo 3 giao tuyến phân biệt là PQ; CD và GF nên chúng song song với nhau.

Hay: PQ // GF // CD, lại có QG // FP(//AB ) nên thiết diện là hình bình hành GQPF.

Đáp án B

Câu 24:

Hình chóp S.ABCD có đáy là hình bình hành ABCD. Giả sử M thuộc đoạn thẳng SB. Mặt phẳng (ADM) cắt hình chóp S.ABCD theo thiết diện là hình:

A.tam giác

B. hình thang

C. hình bình hành

D.hình thoi

Xem đáp án

Do AD//BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC, đường thẳng này cắt SC tại N.

Ta có MN//AD ( vì cùng // BC). Vậy thiết diện là hình thang AMND.

Đáp án B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 11 Bài 3: Đường thẳng và mặt phẳng song song (có đáp án)

Trắc nghiệm Toán 11 Bài 3: Đường thẳng và mặt phẳng song song (phần 1) (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương