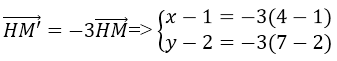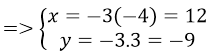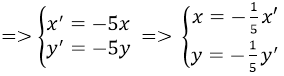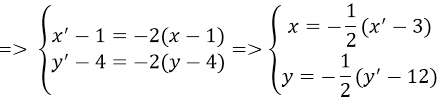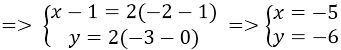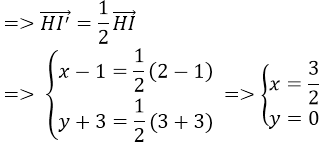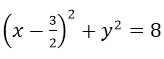Trắc nghiệm Toán 11 Bài 7: Phép vị tự (phần 1) (có đáp án)
-
789 lượt thi
-
22 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hai đường thẳng d và d’ song song với nhau. Tìm mệnh đề đúng:
 Xem đáp án
Xem đáp án
Lấy điểm A, A’ bất kì lần lượt trên d và d’.
Trên đường thẳng AA’ lấy điểm I bất kì, đặt IA'/IA = k.
Khi đó, phép vị tự tâm I tỉ số k biến A thành A’, biến đường thẳng d thành đường thẳng d’.
Vì A và A’ là 2 điểm bất kì trên d và d’ nên có vô số phép vị tự biến d thành d’
Đáp án C
Câu 2:
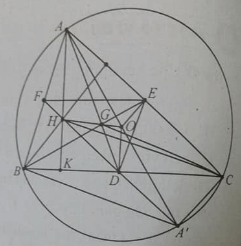
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự tâm G tỉ số -1/2 biến:
 Xem đáp án
Xem đáp án
Vì G là trọng tâm tam giác ABC nên:
⇒ phép vị tự tâm G tỉ số -1/2 biến A thành D.
Đáp án B.
Câu 3:
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
 Xem đáp án
Xem đáp án
Theo tính chất trọng tâm tam giác ta có:
Do đó, phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F
⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
Câu 4:
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến thành
 Xem đáp án
Xem đáp án
Gọi A’ là điểm đối xứng với A qua tâm O.
*Chứng minh BHCA’ là hình bình hành:
Ta có: BH// CA' ( vì cùng vuông góc CA)
A'B // CH ( vì cùng vuông góc với AB)
Do đó, tứ giác BHCA' là hình bình hành, có 2 đường chéo A'H và BC cắt nhau tại trung điểm mỗi đường
Mà D là trung điểm của BC nên D là trung điểm của A'H.
Suy ra H, A', D thẳng hàng và DO là đường trung bình của tam giác AHA’
⇒ ⇒ phép vị tự tâm G tỉ số -1/2 biến thành .
Đáp án B
Câu 5:
Trong mặt phẳng tọa độ Oxy phép vị tự H(1;2) tỉ số k = -3 điểm M(4;7) biến thành điểm M’ có tọa độ
 Xem đáp án
Xem đáp án
Phép vị tự H(1;2) tỉ số k = -3 điểm M(4;7) biến thành điểm M’ nên :
⇒ M'(-8;-13)
Đáp án C
Câu 6:
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình : 3x + y + 6 = 0. Qua phép vị tự tâm O(0;0) tỉ số k = 2, đường thẳng d biến thành đường thẳng d’ có phương trình.
 Xem đáp án
Xem đáp án
Phương trình đường thẳng d: 3x + y + 6 = 0
Lấy M(-2;0) thuộc d.
* Phép vị tự tâm O (0;0) tỉ số k = 2 biến d thành d’, trong đó d' // hoặc trùng với d.
Do đó, d’ có dạng là 3x + y + c = 0
+ Phép vị tự biến M thành M’ nên
M'(-4; 0)
Vì M thuộc d nên M’ thuộc d’, thay tọa độ M’ vào d’ ta được:
3.(-4) + 0 + c = 0 nên c = 12
Phương trình đường thẳng d’: 3x + y + 12 = 0
Chọn đáp án D
Câu 7:
Trong mặt phẳng tọa độ Oxy cho đường (C) có phương trình . Qua phép vị tự tâm H(1;3) tỉ số k = -2, đường tròn (C) biến thành đường tròn (C’) có phương trình.
 Xem đáp án
Xem đáp án
tâm I(2;-3); bán kính R=4
Bán kính R’= |k|. R = |-2| . 4 = 8
Vậy phương trình đường tròn (C') là:
Hay
Đáp án C
Câu 8:
Cho hai đường thẳng d và d’ cắt nhau. Có bao nhiêu phép vị tự biến d thành d’?
 Xem đáp án
Xem đáp án
Không có phép vị tự nào biến d thành d’ (Phép vị tự biến một đường thẳng thành đường thẳng song song hoặc trùng với nó).
Đáp án A
Câu 9:
Cho hai đường tròn (O;R) và (O’;R) (O không trùng với O’). Có bao nhiêu phép vị tự biến (O) thành (O’)?
 Xem đáp án
Xem đáp án
Vì R' = R nên
Nhưng vì hai tâm O và O' là khác nhau nên k = -1
Vậy có một phép vị tự duy nhất, tâm vị tự là trung điểm OO’, tỉ số vị tự là k = -1.
Đáp án B
Câu 10:
Có bao nhiêu phép vị tự biến một đường tròn thành chính nó?
 Xem đáp án
Xem đáp án
Gọi O là tâm đường tròn
Để qua phép vị tự V biến đường tròn (C) thành chính nó thì sẽ biến tâm đường tròn O thành chính nó.
Suy ra, tâm vị tự chính là tâm đường tròn.
Vì R' = R nên k = 1 hoặc k= -1
* Vậy có hai phép vị tự thỏa mãn :
+ Phép vị tự tâm O tỉ số 1 và phép vị tự tâm O tỉ số - 1
Đáp án C
Câu 11:
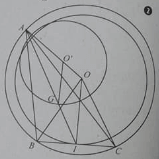
Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC , G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây?
 Xem đáp án
Xem đáp án
B, C cố định nên trung điểm I của BC cũng cố định.
G là trọng tâm tam giác ABC nên ta có
⇒ có phép vị tự I tỉ số k = 1/3 biến A thành G.
A chạy trên (O) nên G chạy trên (O’) ảnh của O qua phép vị tự trên.
Đáp án C
Câu 12:
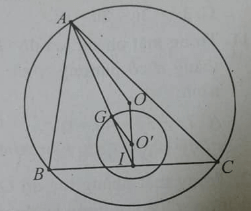
Cho tam giác ABC nội tiếp đường tròn (O;R). Điểm A cố định, dây BC có độ dài bằng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có tam giác OBC đều, đường cao OI = (R√3)/2
⇒ I chạy trên đường tròn tâm O bán kính (R√3)/2.
Vì A cố định, G là trọng tâm tam giác ABC nên
⇒ có phép vị tự tâm A tỉ số k = 2/3 biến đường tròn (O;(R√3)/2) thành đường tròn (O';R’) với
Chọn đáp án C
Câu 13:
Cho hình thang ABCD có AD // BC và AD = 2 BC. Gọi O là giao điểm hai đường chéo hình thang. Phép vị tự tâm A biến C thành O có tỉ số vị tự là:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 14:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ có tọa độ
 Xem đáp án
Xem đáp án
Vì phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ nên :
⇒ M'(12; -9)
Đáp án D
Câu 15:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;2) tỉ số k = 5, biến điểm M(2;-3) thành điểm M’ có tọa độ:
 Xem đáp án
Xem đáp án
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
Suy ra M’(6; -23).
Đáp án C
Câu 16:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(0;2) tỉ số k = -1/2 , biến điểm M(12;-3) thành điểm M’ có tọa độ:
 Xem đáp án
Xem đáp án
Vì phép vị tự tâm I(0;2) tỉ số k = -1/2 , biến điểm M(12;-3) thành điểm M’ nên :
Đáp án B
Câu 17:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -5, biến đường thẳng d có phương trình : 2x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:
 Xem đáp án
Xem đáp án
Phép vị tự tâm O(0; 0) tỉ số k = -5, biến M(x; y) thuộc d thành M’(x’, y’) thuộc d’ ⇒
Thay vào phương trình d ta được:
⇒ phương trình của d’ là 2x + 3y + 20 = 0
Đáp án D
Câu 18:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;4) tỉ số k = -2, biến đường thẳng d có phương trình : 7x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:
 Xem đáp án
Xem đáp án
Phép vị tự tâm I (1; 4) tỉ số k = -2, biến M(x; y) thuộc d thành M’(x’;y’) thuộc d'
⇒
Thay vào phương trình d ta được
⇒ d' có phương trình là: 7x + 3y - 49 = 0.
Đáp án A
Câu 19:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -2, biến đường tròn (C) có phương trình: thành đường tròn (C’) có phương trình:
 Xem đáp án
Xem đáp án
Đường tròn (C) có tâm O(0.0) và bán kính R =3.
Vì tâm vị tự trùng với tâm đường tròn nên: phép vị tự tâm O(0; 0) tỉ số k = -2 biến tâm O của (C) thành O
và bán kính R ' = | -2| . 3 = 6
⇒ phương trình (C’) là
Đáp án B
Câu 20:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = 2 biến đường tròn (C) có phương trình: thành đường tròn (C’) có phương trình
 Xem đáp án
Xem đáp án
(C) ⇒.
Đường tròn (C) có tâm I( -2; -3), bán kính R= 5
Phép vị tự tâm O(0; 0) tỉ số k = 2 biến tâm I(-2; -3) của (C) thành I’(-4; -6).
và bán kính R’ = 2. 5 = 10
⇒ phương trình (C’) là:
Đáp án C
Câu 21:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;0) tỉ số k = 2, biến đường tròn (C) có phương trình : thành đường tròn (C’) có phương trình
 Xem đáp án
Xem đáp án
(C) ⇒ .
Đường tròn (C) có tâm I(-2; -3) và bán kính R= 5
Phép vị tự tâm H(1; 0) tỉ số k = 2, biến tâm I(-2; -3) của (C) thành I’(x;y)
⇒
và bán kính R’ =2.5 = 10
⇒ Phương trình (C’) là:
Đáp án B
Câu 22:
Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k = 1/2, biến đường tròn (C) có phương trình : thành đường tròn (C’) có phương trình:
 Xem đáp án
Xem đáp án
Đường tròn (C) có tâm I(2; 3) và bán kính
Phép vị tự tâm H (1; -3) tỉ số k = 1/2, biến tâm I(2; 3) của (C) thành I’(x; y)
và
⇒ phương trình (C’) là:
Đáp án D